人教版七年级上数学1.4.1有理数的乘法课件(第一课时 20张)
文档属性
| 名称 | 人教版七年级上数学1.4.1有理数的乘法课件(第一课时 20张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 00:00:00 | ||
图片预览






文档简介
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
再例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
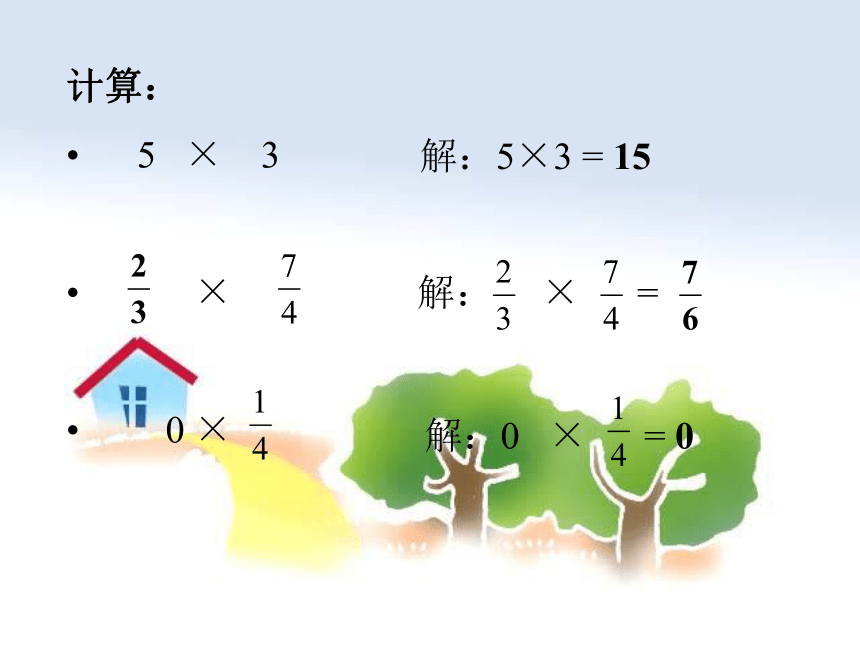
解:5×3 = 15
解: × =
计算:
5 × 3
×
0 ×
解:0 × = 0
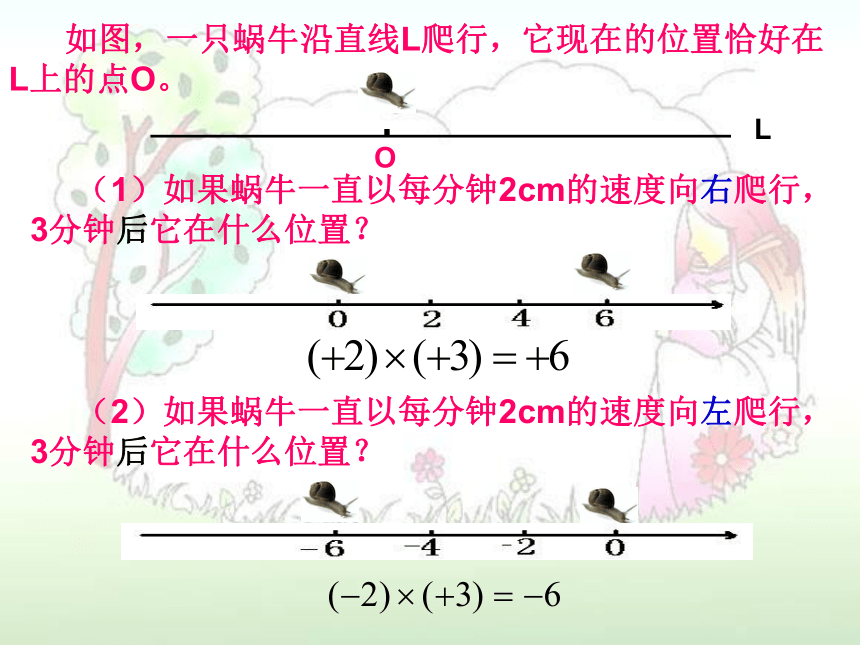
如图,一只蜗牛沿直线L爬行,它现在的位置恰好在
L上的点O。
O
(1)如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟后它在什么位置?
(2)如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟后它在什么位置?
L
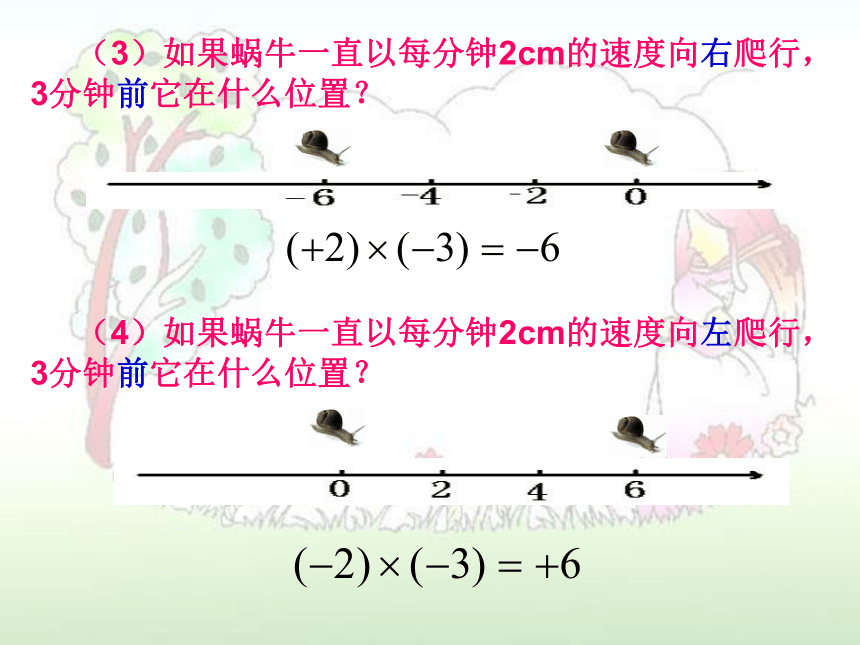
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟后它在什么位置?
(3)如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
观察(1)-(4)式,根据你对有理数乘法的思考,填空:
正数乘正数积为___数;
负数乘正数积为___数;
正数乘负数积为___数;
负数乘负数积为___数;
乘积的绝对值等于各乘数绝对值的___.
正
正
负
负
积
综合如下:
(1) 2×3=6
(2)(-2)×3= -6
(3) 2×(-3)= -6
(4)(-2)×(-3)=6
(5) 被乘数或乘数为0时,结果是0
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。
练习1:确定下列积的符号:
(1) 5×(-3)
(2) (-4)×6
(3) (-7)×(-9)
(4) 0.5×0.7
积的符号为负
积的符号为负
积的符号为正
积的符号为正
例如 (-5) ×(- 3)
(同号两数相乘)
(-5)×(- 3)= +( )
(得正)
5×3 = 15
(把绝对值相乘)
∴(-5)×(-3)=15
又如:(-7)×4
(异号两数相乘)
(-7)×4= -( )
(得负)
7×4=28
(把绝对值相乘)
∴(-7)×4=-28
注意:有理数相乘,先确定积的符号,在确定积的值
解:(1) (-3) ×9 =
-27
注意:乘积是1的两个数互为倒数.一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。
(3) 7 × (-1) =
(4) (-0.8)× 1 =
- 7
- 0.8
例1 计算:
(1) (-3)×9 (2)( )×
(3) 7 ×(-1) (4) (-0.8)× 1
(2) ( ) × =
解:(-6)×3=
-18
答:气温下降18 ℃.
-54
-24
6
0
1.计算(口答):
(1)6×(-9)=
(2)(-4)×6=
(3)(-6)×(-1)=
(4)(-6) ×0=
(5) ×(- )=
(6)(- ) × =
小结:
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。
2.如何进行两个有理数的运算:
先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零。
一,是同号相乘,所乘得的结果应为正。
二,可以先得到(-7)×(-4)= +( )的判断
三,把绝对值相乘,得出结果。
所以有
(-7)×(-4)=+(28) 的结果
一,是异号相乘,所乘得的结果应为负。
二,可以先得到(-7)× 4 = -( ) 的判断
三,把绝对值相乘,得出结果。
所以有
(-7)×4= -(28)的结果
③7×(-1);
④ (-0.8)×1.
;
解:① (-3)×(-9)
( 3×9)
=27
③7×(-1);
④ (-0.8)×1.
;
②
=
=
③ 7×(-1)=
(7 ×1)
=-7
④ (-0.8)×1=
(0.8 ×1)
-
=-0.8
-
=+
+
+
-
-
-54
-54
6
0
54
-6
-6
0
计算:
解:原式=
=
这个解答正确么?你认为应该怎么做?答案是多少呢?
-
-
1)如果a×b=0,则这两个数 ( )
A 都等于0, B 有一个等于0,另一个不等于0;
C 至少有一个等于0, D 互为相反数
2)已知-3a是一个负数,则 ( )
A a>0 B a<0 C a≥0 D a≤0
C
A
A 两个数均为0, B 两个数中一个为0
C 两数互为相反数, D 两数互为相反数,但不为0。
D
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
再例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟前它在什么位置?
(3)如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
再例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
例如 (-5) ×(- 3)
(同号两数相乘)
(-5)×(- 3)= +( )
(得正)
5×3 = 15
(把绝对值相乘)
∴(-5)×(-3)=15
又如:(-7)×4
(异号两数相乘)
(-7)×4= -( )
(得负)
7×4=28
(把绝对值相乘)
∴(-7)×4=-28
注意:有理数相乘,先确定积的符号,在确定积的值
解:① (-3)×(-9)
( 3×9)
=27
③7×(-1);
④ (-0.8)×1.
;
②
=
=
③ 7×(-1)=
(7 ×1)
=-7
④ (-0.8)×1=
(0.8 ×1)
-
=-0.8
-
=+
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
再例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
+
+
-
-
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
再例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟前它在什么位置?
(3)如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
观察(1)-(4)式,根据你对有理数乘法的思考,填空:
正数乘正数积为___数;
负数乘正数积为___数;
正数乘负数积为___数;
负数乘负数积为___数;
乘积的绝对值等于各乘数绝对值的___.
正
正
负
负
积
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
再例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
解:(1) (-3) ×9 =
-27
注意:乘积是1的两个数互为倒数.一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。
(3) 7 × (-1) =
(4) (-0.8)× 1 =
- 7
- 0.8
例1 计算:
(1) (-3)×9 (2)( )×
(3) 7 ×(-1) (4) (-0.8)× 1
(2) ( ) × =
-54
-24
6
0
1.计算(口答):
(1)6×(-9)=
(2)(-4)×6=
(3)(-6)×(-1)=
(4)(-6) ×0=
(5) ×(- )=
(6)(- ) × =
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
一,是同号相乘,所乘得的结果应为正。
二,可以先得到(-7)×(-4)= +( )的判断
三,把绝对值相乘,得出结果。
所以有
(-7)×(-4)=+(28) 的结果
一,是异号相乘,所乘得的结果应为负。
二,可以先得到(-7)× 4 = -( ) 的判断
三,把绝对值相乘,得出结果。
所以有
(-7)×4= -(28)的结果
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
一,是异号相乘,所乘得的结果应为负。
二,可以先得到(-7)× 4 = -( ) 的判断
三,把绝对值相乘,得出结果。
所以有
(-7)×4= -(28)的结果
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决
③7×(-1);
④ (-0.8)×1.
;
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
例如计算(-7)×4
例题讲解
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
解:① (-3)×(-9)
( 3×9)
=27
③7×(-1);
④ (-0.8)×1.
;
②
=
=
③ 7×(-1)=
(7 ×1)
=-7
④ (-0.8)×1=
(0.8 ×1)
-
=-0.8
-
=+
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
再例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
解:5×3 = 15
解: × =
计算:
5 × 3
×
0 ×
解:0 × = 0
如图,一只蜗牛沿直线L爬行,它现在的位置恰好在
L上的点O。
O
(1)如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟后它在什么位置?
(2)如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟后它在什么位置?
L
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟后它在什么位置?
(3)如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
观察(1)-(4)式,根据你对有理数乘法的思考,填空:
正数乘正数积为___数;
负数乘正数积为___数;
正数乘负数积为___数;
负数乘负数积为___数;
乘积的绝对值等于各乘数绝对值的___.
正
正
负
负
积
综合如下:
(1) 2×3=6
(2)(-2)×3= -6
(3) 2×(-3)= -6
(4)(-2)×(-3)=6
(5) 被乘数或乘数为0时,结果是0
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。
练习1:确定下列积的符号:
(1) 5×(-3)
(2) (-4)×6
(3) (-7)×(-9)
(4) 0.5×0.7
积的符号为负
积的符号为负
积的符号为正
积的符号为正
例如 (-5) ×(- 3)
(同号两数相乘)
(-5)×(- 3)= +( )
(得正)
5×3 = 15
(把绝对值相乘)
∴(-5)×(-3)=15
又如:(-7)×4
(异号两数相乘)
(-7)×4= -( )
(得负)
7×4=28
(把绝对值相乘)
∴(-7)×4=-28
注意:有理数相乘,先确定积的符号,在确定积的值
解:(1) (-3) ×9 =
-27
注意:乘积是1的两个数互为倒数.一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。
(3) 7 × (-1) =
(4) (-0.8)× 1 =
- 7
- 0.8
例1 计算:
(1) (-3)×9 (2)( )×
(3) 7 ×(-1) (4) (-0.8)× 1
(2) ( ) × =
解:(-6)×3=
-18
答:气温下降18 ℃.
-54
-24
6
0
1.计算(口答):
(1)6×(-9)=
(2)(-4)×6=
(3)(-6)×(-1)=
(4)(-6) ×0=
(5) ×(- )=
(6)(- ) × =
小结:
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。
2.如何进行两个有理数的运算:
先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零。
一,是同号相乘,所乘得的结果应为正。
二,可以先得到(-7)×(-4)= +( )的判断
三,把绝对值相乘,得出结果。
所以有
(-7)×(-4)=+(28) 的结果
一,是异号相乘,所乘得的结果应为负。
二,可以先得到(-7)× 4 = -( ) 的判断
三,把绝对值相乘,得出结果。
所以有
(-7)×4= -(28)的结果
③7×(-1);
④ (-0.8)×1.
;
解:① (-3)×(-9)
( 3×9)
=27
③7×(-1);
④ (-0.8)×1.
;
②
=
=
③ 7×(-1)=
(7 ×1)
=-7
④ (-0.8)×1=
(0.8 ×1)
-
=-0.8
-
=+
+
+
-
-
-54
-54
6
0
54
-6
-6
0
计算:
解:原式=
=
这个解答正确么?你认为应该怎么做?答案是多少呢?
-
-
1)如果a×b=0,则这两个数 ( )
A 都等于0, B 有一个等于0,另一个不等于0;
C 至少有一个等于0, D 互为相反数
2)已知-3a是一个负数,则 ( )
A a>0 B a<0 C a≥0 D a≤0
C
A
A 两个数均为0, B 两个数中一个为0
C 两数互为相反数, D 两数互为相反数,但不为0。
D
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
再例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟前它在什么位置?
(3)如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
再例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
例如 (-5) ×(- 3)
(同号两数相乘)
(-5)×(- 3)= +( )
(得正)
5×3 = 15
(把绝对值相乘)
∴(-5)×(-3)=15
又如:(-7)×4
(异号两数相乘)
(-7)×4= -( )
(得负)
7×4=28
(把绝对值相乘)
∴(-7)×4=-28
注意:有理数相乘,先确定积的符号,在确定积的值
解:① (-3)×(-9)
( 3×9)
=27
③7×(-1);
④ (-0.8)×1.
;
②
=
=
③ 7×(-1)=
(7 ×1)
=-7
④ (-0.8)×1=
(0.8 ×1)
-
=-0.8
-
=+
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
再例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
+
+
-
-
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
再例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟前它在什么位置?
(3)如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
观察(1)-(4)式,根据你对有理数乘法的思考,填空:
正数乘正数积为___数;
负数乘正数积为___数;
正数乘负数积为___数;
负数乘负数积为___数;
乘积的绝对值等于各乘数绝对值的___.
正
正
负
负
积
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
再例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
解:(1) (-3) ×9 =
-27
注意:乘积是1的两个数互为倒数.一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。
(3) 7 × (-1) =
(4) (-0.8)× 1 =
- 7
- 0.8
例1 计算:
(1) (-3)×9 (2)( )×
(3) 7 ×(-1) (4) (-0.8)× 1
(2) ( ) × =
-54
-24
6
0
1.计算(口答):
(1)6×(-9)=
(2)(-4)×6=
(3)(-6)×(-1)=
(4)(-6) ×0=
(5) ×(- )=
(6)(- ) × =
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
一,是同号相乘,所乘得的结果应为正。
二,可以先得到(-7)×(-4)= +( )的判断
三,把绝对值相乘,得出结果。
所以有
(-7)×(-4)=+(28) 的结果
一,是异号相乘,所乘得的结果应为负。
二,可以先得到(-7)× 4 = -( ) 的判断
三,把绝对值相乘,得出结果。
所以有
(-7)×4= -(28)的结果
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-7)×(-4)
感受法则、理解法则:
例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
一,是异号相乘,所乘得的结果应为负。
二,可以先得到(-7)× 4 = -( ) 的判断
三,把绝对值相乘,得出结果。
所以有
(-7)×4= -(28)的结果
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决
③7×(-1);
④ (-0.8)×1.
;
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
例如计算(-7)×4
例题学习
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
问题:怎样计算
(1)
(2)
例2 用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3 km后,气温有什么变化?
感受法则、理解法则:
例如计算(-7)×4
例题讲解
计算:
①(-3)×(-9); ②(- )×
1.确定下列两数积的符号(口答)
①5× (-3); ②(-4) ×6;
③(-7) ×(-9); ④0.5×0.7.
2.口算:
①6 × (-9) = ②(-6) ×(-9) =
③(-6) ×9= ④(-6) ×1=
⑤(-6) ×(-1) = ⑥6 ×(-1) =
⑦(-6) ×0 = ⑧0×(-6)=
课堂练习(正误辨析)
你能看出下面计算有误么?
课堂练习(选择题)
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
解:① (-3)×(-9)
( 3×9)
=27
③7×(-1);
④ (-0.8)×1.
;
②
=
=
③ 7×(-1)=
(7 ×1)
=-7
④ (-0.8)×1=
(0.8 ×1)
-
=-0.8
-
=+
