华师大版八上:12.3 乘法公式 教案(共2课时)
文档属性
| 名称 | 华师大版八上:12.3 乘法公式 教案(共2课时) |  | |
| 格式 | doc | ||
| 文件大小 | 130.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-02 18:29:46 | ||
图片预览

文档简介
课题 1.两数和乘以这两数的差 课时 1课时 上课时间
教学目标 1.知识与技能
(1)理解两数和乘以这两数的差的公式.
(2)能熟练进行两数和乘以这两数的差的运算.
2.过程与方法
(1)通过探索两数和乘以这两数的差的公式,让学生体会数形结合的思想方法和总结归纳的数学能力.
(2)在进行两数和乘以这两数的差的运算中培养学生的观察分析和计算能力.
3.情感、态度与价值观
(1)在学生自主探究中,感受成功的乐趣,增强自信心,培养创新意识和能力.
(2)在分组交流中提高学生的协作意识,养成独立思考和合作结合的习惯.
教学 重难点 重点:掌握两数和乘以这两数的差的公式,会进行两数和乘以这两数的差的运算.
难点:探究两数和乘以这两数的差的公式的思维过程.
教学活动设计 二次设计
课堂导入 思考下面的问题:
1.多项式与多项式相乘的方法?
2.计算:
(1)(x+3y)(x-3y);(2)(x+2)(x-2).
3.长方形的长为a+b,宽为a-b,你可以求出它的面积吗?
探索新知 合作探究 自学指导
1.根据多项式乘以多项式的法则计算:(a+b)(a-b)= ,?
2.观察算式的特点: ,观察结果的特征: .?
3.归纳两数和乘以这两数的差的公式: .?
4.(a+3)(a-3)中分别是哪两个数的和与差,根据公式应写成什么形式?(-2x-y)(2x-y)中怎样运用加法交换律整理为两数和乘以这两数的差的形式?结合例1学习两数和乘以这两数的差的公式的运用方法.
5.计算教材图12.3.1中图形面积,进一步体会公式.
6.自学课本P30~32,用公式表示两数和乘以这两数的差的运算方法.
学生看书,教师巡视,老师督促每一位学生认真、紧张的自学,鼓励学生质疑问难.
合作探究
1.讨论
小组讨论自学指导中出现疑问的地方.
2.组织学生根据多项式与多项式相乘的运算法则推理归纳两数和乘以这两数的差的公式.
3.运用数形结合的方法探索验证两数和乘以这两数的差的公式.
4.结合例1组织学生探索两数和乘以这两数的差的公式的运用及注意问题.
5.结合例2组织学生学习公式在简便计算中的运用.
6.结合例3组织学生学习公式在实际问题中的运用.
续表
探索新知 合作探究 教师指导
1.易错点:
(1)对于不满足条件的乘法算式误用两数和乘以这两数的差的公式.
(2)运用公式时忘记整理,误以为谁在前面谁就是第一个数.
2.归纳小结:
两数和乘以这两数的差的公式:(a+b)(a-b)=a2-b2.
3.方法规律:
(1)两数和乘以这两数的差的公式:算式特点:两个多项式的项数相同,既有完全相同的项又有相反的项;结果:相同项的平方减去相反项的平方.
(2)两数和乘以这两数的差的公式运用:1理(整理为两数和与差的积的形式),2套(套用公式展开),3计算(算出最后结果).
当堂训练
1.下列各式中,能用平方差公式计算的是( )
①(7ab-3b)(7ab+3b);②73×94;③(-8+a)(a-8);
④(-15-x)(x-15).
(A)①③ (B)②④ (C)③④ (D)①④
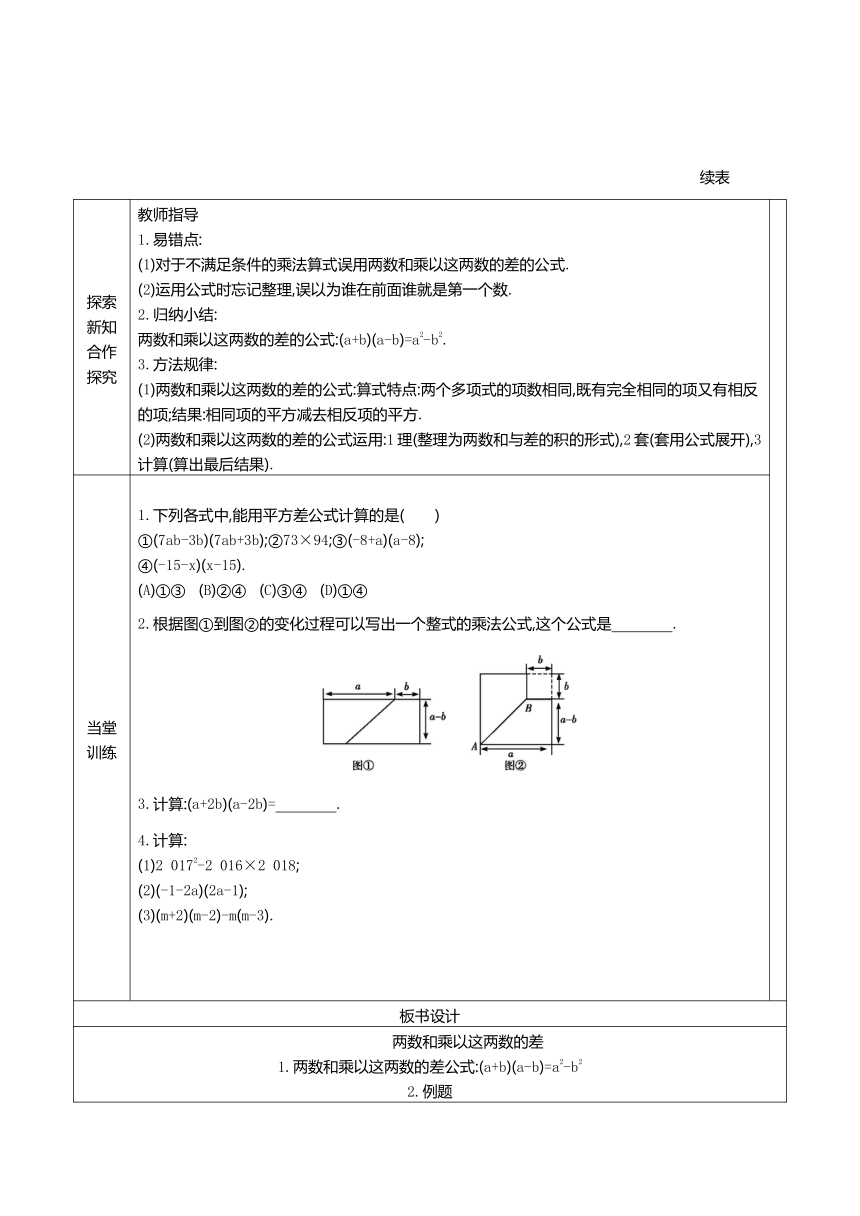
2.根据图①到图②的变化过程可以写出一个整式的乘法公式,这个公式是 .?
3.计算:(a+2b)(a-2b)= .?
4.计算:
(1)2 0172-2 016×2 018;
(2)(-1-2a)(2a-1);
(3)(m+2)(m-2)-m(m-3).
板书设计
两数和乘以这两数的差 1.两数和乘以这两数的差公式:(a+b)(a-b)=a2-b2
2.例题
教学反思
课题 2.两数和(差)的平方 课时 1课时 上课时间
教学目标 1.知识与技能
(1)理解两数和(差)的平方的公式.
(2)能熟练进行两数和(差)的平方的运算.
2.过程与方法
(1)通过探索两数和乘以这两数的差的公式,让学生体会从一般到特殊的基本思想和数形结合的基本方法.
(2)在进行两数和(差)的平方的运算中提高学生的观察分析和计算能力.
3.情感、态度与价值观
(1)在学生自主探究中,感受成功的乐趣,使学生充满自信充满阳光.
(2)在分组交流中提高学生的协作意识,养成合作学习的习惯,体会团队的价值.
教学 重难点 重点:掌握两数和(差)的平方的公式,会进行两数和(差)的平方的运算.
难点:探究两数和(差)的平方公式的思维过程.
教学活动设计 二次设计
课堂导入 思考下面的问题:
1.多项式与多项式相乘的方法?
2.计算:
(1)(x+3y)(x+3y);(2)(x-2)(x-2).
3.正方形的边长为a+b,你可以求出它的面积吗?
探索新知 合作探究 自学指导
1.(a+b)2是2个 相乘,(a+b)2=( )( ).?
根据多项式乘以多项式的法则计算:(a+b)2= .?
2.观察算式的特点:左边是 ,观察结果的特征:右边是 .?
3.归纳两数和的平方公式: .?
4.根据教材图12.3.2分别计算图形的面积,可以得到什么关系?
5.例4中,(2x+3y)2和2a+2是否符合两数和的平方公式?分别对应公式中的a,b这两个数是多少?怎样根据公式计算?
6.把(a-b)2整理为[a+(-b)]2后,你可以根据两数和的平方公式进行计算吗?根据多项式乘以多项式进行计算看结果是否相同.
7.根据自己计算的结果总结两数差的平方公式: .?
8.对应公式结合例5学习两数差的平方公式的运用和注意问题.
9.自学课本P32~34,用公式表示两数和(差)的平方公式的运算方法.
学生看书,教师巡视,老师督促每一位学生认真、紧张的自学,鼓励学生质疑问难.
合作探究
1.讨论
小组讨论自学指导中出现疑问的地方.
2.组织学生根据多项式与多项式相乘的运算法则推理归纳两数和(差)的平方公式.
3.运用数形结合的方法探索验证两数和(差)的平方公式.
续表
探索新知 合作探究 4.结合例4、例5,组织学生探索两数和(差)的平方公式运用及注意问题.
5.拓展讲解公式的综合运用(补充例题:(x+y-z)(x+y+z)).
教师指导
1.易错点:
(1)对于不满足条件的乘法算式误用两数和(差)的平方的公式.
(2)运用公式时忘记两数积的2倍或弄错这一项的符号.
2.归纳小结:
两数和(差)的平方公式:(a±b)2=a2±2ab+b2.
3.方法规律:
(1)两数和(差)的平方公式:算式特点:一个多项式的平方;结果:三项:两项是平方的和,一项是乘积的2倍.
(2)两数和乘以这两数的差的公式运用:1看(两数和还是差),2套(套用对应的公式展开),3计算(算出最后结果).
当堂训练
1.运用乘法公式计算(x+3)2的结果是( )
(A)x2+9 (B)x2-6x+9
(C)x2+6x+9 (D)x2+3x+9
2.下列各式中,能用完全平方公式计算的是( )
(A)(3a-2b)(-2b-3a) (B)(3a+2b)(-3a-2b)
(C)(3a+2b)(-2a-3b) (D)(3a-2b)(3a+2b)
3.(x+b)2=x2+ax+121,则a= ,b= .?
4.计算:
(1)(-2m+n)2;
(2)(-2m-n)2;
(3)(2a+b)2-(2a-b)2.
板书设计
两数和(差)的平方 1.两数和(差)的平方公式:(a±b)2=a2±2ab+b2
2.例题
教学反思
教学目标 1.知识与技能
(1)理解两数和乘以这两数的差的公式.
(2)能熟练进行两数和乘以这两数的差的运算.
2.过程与方法
(1)通过探索两数和乘以这两数的差的公式,让学生体会数形结合的思想方法和总结归纳的数学能力.
(2)在进行两数和乘以这两数的差的运算中培养学生的观察分析和计算能力.
3.情感、态度与价值观
(1)在学生自主探究中,感受成功的乐趣,增强自信心,培养创新意识和能力.
(2)在分组交流中提高学生的协作意识,养成独立思考和合作结合的习惯.
教学 重难点 重点:掌握两数和乘以这两数的差的公式,会进行两数和乘以这两数的差的运算.
难点:探究两数和乘以这两数的差的公式的思维过程.
教学活动设计 二次设计
课堂导入 思考下面的问题:
1.多项式与多项式相乘的方法?
2.计算:
(1)(x+3y)(x-3y);(2)(x+2)(x-2).
3.长方形的长为a+b,宽为a-b,你可以求出它的面积吗?
探索新知 合作探究 自学指导
1.根据多项式乘以多项式的法则计算:(a+b)(a-b)= ,?
2.观察算式的特点: ,观察结果的特征: .?
3.归纳两数和乘以这两数的差的公式: .?
4.(a+3)(a-3)中分别是哪两个数的和与差,根据公式应写成什么形式?(-2x-y)(2x-y)中怎样运用加法交换律整理为两数和乘以这两数的差的形式?结合例1学习两数和乘以这两数的差的公式的运用方法.
5.计算教材图12.3.1中图形面积,进一步体会公式.
6.自学课本P30~32,用公式表示两数和乘以这两数的差的运算方法.
学生看书,教师巡视,老师督促每一位学生认真、紧张的自学,鼓励学生质疑问难.
合作探究
1.讨论
小组讨论自学指导中出现疑问的地方.
2.组织学生根据多项式与多项式相乘的运算法则推理归纳两数和乘以这两数的差的公式.
3.运用数形结合的方法探索验证两数和乘以这两数的差的公式.
4.结合例1组织学生探索两数和乘以这两数的差的公式的运用及注意问题.
5.结合例2组织学生学习公式在简便计算中的运用.
6.结合例3组织学生学习公式在实际问题中的运用.
续表
探索新知 合作探究 教师指导
1.易错点:
(1)对于不满足条件的乘法算式误用两数和乘以这两数的差的公式.
(2)运用公式时忘记整理,误以为谁在前面谁就是第一个数.
2.归纳小结:
两数和乘以这两数的差的公式:(a+b)(a-b)=a2-b2.
3.方法规律:
(1)两数和乘以这两数的差的公式:算式特点:两个多项式的项数相同,既有完全相同的项又有相反的项;结果:相同项的平方减去相反项的平方.
(2)两数和乘以这两数的差的公式运用:1理(整理为两数和与差的积的形式),2套(套用公式展开),3计算(算出最后结果).
当堂训练
1.下列各式中,能用平方差公式计算的是( )
①(7ab-3b)(7ab+3b);②73×94;③(-8+a)(a-8);
④(-15-x)(x-15).
(A)①③ (B)②④ (C)③④ (D)①④
2.根据图①到图②的变化过程可以写出一个整式的乘法公式,这个公式是 .?
3.计算:(a+2b)(a-2b)= .?
4.计算:
(1)2 0172-2 016×2 018;
(2)(-1-2a)(2a-1);
(3)(m+2)(m-2)-m(m-3).
板书设计
两数和乘以这两数的差 1.两数和乘以这两数的差公式:(a+b)(a-b)=a2-b2
2.例题
教学反思
课题 2.两数和(差)的平方 课时 1课时 上课时间
教学目标 1.知识与技能
(1)理解两数和(差)的平方的公式.
(2)能熟练进行两数和(差)的平方的运算.
2.过程与方法
(1)通过探索两数和乘以这两数的差的公式,让学生体会从一般到特殊的基本思想和数形结合的基本方法.
(2)在进行两数和(差)的平方的运算中提高学生的观察分析和计算能力.
3.情感、态度与价值观
(1)在学生自主探究中,感受成功的乐趣,使学生充满自信充满阳光.
(2)在分组交流中提高学生的协作意识,养成合作学习的习惯,体会团队的价值.
教学 重难点 重点:掌握两数和(差)的平方的公式,会进行两数和(差)的平方的运算.
难点:探究两数和(差)的平方公式的思维过程.
教学活动设计 二次设计
课堂导入 思考下面的问题:
1.多项式与多项式相乘的方法?
2.计算:
(1)(x+3y)(x+3y);(2)(x-2)(x-2).
3.正方形的边长为a+b,你可以求出它的面积吗?
探索新知 合作探究 自学指导
1.(a+b)2是2个 相乘,(a+b)2=( )( ).?
根据多项式乘以多项式的法则计算:(a+b)2= .?
2.观察算式的特点:左边是 ,观察结果的特征:右边是 .?
3.归纳两数和的平方公式: .?
4.根据教材图12.3.2分别计算图形的面积,可以得到什么关系?
5.例4中,(2x+3y)2和2a+2是否符合两数和的平方公式?分别对应公式中的a,b这两个数是多少?怎样根据公式计算?
6.把(a-b)2整理为[a+(-b)]2后,你可以根据两数和的平方公式进行计算吗?根据多项式乘以多项式进行计算看结果是否相同.
7.根据自己计算的结果总结两数差的平方公式: .?
8.对应公式结合例5学习两数差的平方公式的运用和注意问题.
9.自学课本P32~34,用公式表示两数和(差)的平方公式的运算方法.
学生看书,教师巡视,老师督促每一位学生认真、紧张的自学,鼓励学生质疑问难.
合作探究
1.讨论
小组讨论自学指导中出现疑问的地方.
2.组织学生根据多项式与多项式相乘的运算法则推理归纳两数和(差)的平方公式.
3.运用数形结合的方法探索验证两数和(差)的平方公式.
续表
探索新知 合作探究 4.结合例4、例5,组织学生探索两数和(差)的平方公式运用及注意问题.
5.拓展讲解公式的综合运用(补充例题:(x+y-z)(x+y+z)).
教师指导
1.易错点:
(1)对于不满足条件的乘法算式误用两数和(差)的平方的公式.
(2)运用公式时忘记两数积的2倍或弄错这一项的符号.
2.归纳小结:
两数和(差)的平方公式:(a±b)2=a2±2ab+b2.
3.方法规律:
(1)两数和(差)的平方公式:算式特点:一个多项式的平方;结果:三项:两项是平方的和,一项是乘积的2倍.
(2)两数和乘以这两数的差的公式运用:1看(两数和还是差),2套(套用对应的公式展开),3计算(算出最后结果).
当堂训练
1.运用乘法公式计算(x+3)2的结果是( )
(A)x2+9 (B)x2-6x+9
(C)x2+6x+9 (D)x2+3x+9
2.下列各式中,能用完全平方公式计算的是( )
(A)(3a-2b)(-2b-3a) (B)(3a+2b)(-3a-2b)
(C)(3a+2b)(-2a-3b) (D)(3a-2b)(3a+2b)
3.(x+b)2=x2+ax+121,则a= ,b= .?
4.计算:
(1)(-2m+n)2;
(2)(-2m-n)2;
(3)(2a+b)2-(2a-b)2.
板书设计
两数和(差)的平方 1.两数和(差)的平方公式:(a±b)2=a2±2ab+b2
2.例题
教学反思
