苏科版七年级上册数学第5章 走进图形世界数学活动 设计包装纸箱 教案
文档属性
| 名称 | 苏科版七年级上册数学第5章 走进图形世界数学活动 设计包装纸箱 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 00:00:00 | ||
图片预览


文档简介
“设计包装纸箱”活动设计
活动目的:
1.经历“从实际问题抽象出数学问题、建立数学模型、综合运用已有知识解决问题”的过程,
2.通过观察、操作、计算、比较、猜想等活动,提升数学活动的价值,增强数学活动经验
3.在探索活动过程中,体会从特殊到一般、转化的数学思想。
活动重点:
1.经历实际问题数学化——建立数学模型——解决问题的过程.
2.丰富空间观念,发展空间想象能力.
活动难点:对用料最省问题的探讨
活动时间:45—50分钟
活动方式:自主探索与小组合作结合
预备知识:长方体的棱长与表面积的关系
活动准备:
长方体模型(长、宽、高分别为3cm、2cm、1cm)(学生课前制作好;每个同学准备6个或者以小组为单位,每组共制作30个)
主要过程:
(一)预习自学
1、已知某个长方体的长、宽、高分别为3cm、2cm、1cm ,若想用包装纸进行包装(不考虑包装纸接口重叠部分),则包装纸至少为多大?(说明:本节数学活动都不考虑包装纸接口重叠部分。下面不再提醒。)
(熟练进行长方体的表面积计算,为下面的活动铺垫)
2、若上述长方体的个数为2,请你设计一种包装纸箱包装,使该纸箱所用材料尽可能少,则包装纸至少为多大?(设计意图:当包装多个长方体物品时,学生容易感知不同的摆放方案,所形成的大长方体棱长有长有短,从而表面积有大小,包装纸材料可以尽可能少,激发学生动手操作并记录数据进行比较的兴趣)
(预习自学环节可以设计到活动学案中,让学生课前完成。课堂上,在问题情境探索的开始部分,引导学生意识到要解决30个相同尺寸的长方体包装纸箱如何设计用料最省的问题,可以先列举出当数量是1,2个时,是怎样设计的,适时汇报课前预习的情况。)
(二)创设情境,引入课题
1.展示一组包装箱(袋),提问:厂家在设计产品的包装箱时,要考虑哪些因素?
(学生可能从形状、材料、美观、成本,有创意、接缝处卡纸的设计等方面回答问题。)
2.形状一般以长方体居多,材料以纸质较多,注重环保,并且我们总希望能利用有限的资源创造出尽可能大的收益。比如考虑到制作成本,厂家会考虑怎样用料较省。
3.现在有30个长、宽、高分别为3cm、2cm、1cm的橡皮块。请你帮厂家设计一种包装纸箱包装,使该纸箱所用材料尽可能少。(说明:橡皮块用课前制作好的长方体代替)
教师点拨:橡皮块类似数学中的模型长方体,一个橡皮块包装材料至少为多少呢?
生回答,与此同时起到复习长方体表面积的计算方法的作用。长方体的表面积等于2×(长×宽+长×高+宽×高)。
点拨:解决数量多的一类问题时,我们通常先列举,再归纳,比如设计两个橡皮块的包装纸,怎样用料最省?
(三)活动1:个数较少情形1——长方体的个数是2
观察操作:自主探索,在表格里填写设计方案,个别展示,回答问题。
(课前学生自学过,可以快速给出拼法示意图,并能计算出长方体的表面积。)
计算比较:我们发现,“计算包装纸的最小面积”的问题实际上可以转化为“计算拼成的大长方体的表面积”问题来解决。
猜想结论:可以发现,如果相同长方体橡皮块的数量一定,当其重叠部分的面积较大时,包装纸箱的表面积较小。
(四)活动2:个数较少情形2——长方体的个数是3
问题1:它们拼成多少种不同的拼接方式?
(学生容易给出3种拼法,将3×2的面重合,3×1的面重合,2×1的面重合。通过计算,得出用料较省的拼法是将3×2的面重合。
教师引导学生说出拼的方式,其实是原来的小长方体的长、宽、高分别扩大了3倍。
问题2:小明同学的拼接方式中有这样一种情形:
2个小长方体在下面,一个在上面,拼接了2层。对此,你有何看法?
(学生通过操作,计算,比较,发现此时的表面积比较大,不是较省的方案。)
问题3:通过上面的探索,我们发现:要想包装纸尽可能少,那么这些小长方体应该拼接成什么形状?(长方体)
问题4:是否还有其他的拼法?如图。
通过计算,发现这样的表面积跟之前的最小方案表面积一样。
猜想结论:同样地,观察示意图,可以发现,如果相同长方体橡皮块的数量一定,当其重叠部分的面积较大时,包装纸箱的表面积较小。
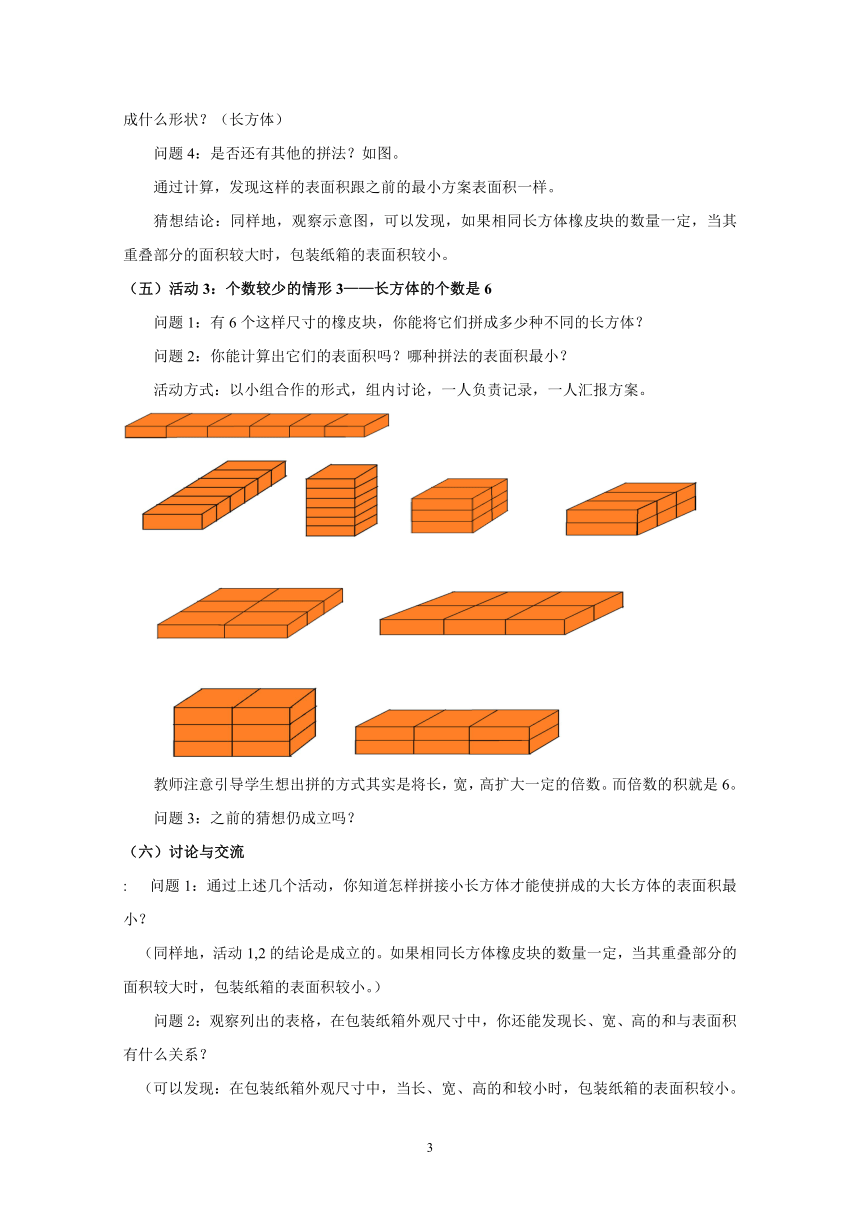
(五)活动3:个数较少的情形3——长方体的个数是6
问题1:有6个这样尺寸的橡皮块,你能将它们拼成多少种不同的长方体?
问题2:你能计算出它们的表面积吗?哪种拼法的表面积最小?
活动方式:以小组合作的形式,组内讨论,一人负责记录,一人汇报方案。
教师注意引导学生想出拼的方式其实是将长,宽,高扩大一定的倍数。而倍数的积就是6。
问题3:之前的猜想仍成立吗?
(六)讨论与交流
: 问题1:通过上述几个活动,你知道怎样拼接小长方体才能使拼成的大长方体的表面积最小?
(同样地,活动1,2的结论是成立的。如果相同长方体橡皮块的数量一定,当其重叠部分的面积较大时,包装纸箱的表面积较小。)
问题2:观察列出的表格,在包装纸箱外观尺寸中,你还能发现长、宽、高的和与表面积有什么关系?
(可以发现:在包装纸箱外观尺寸中,当长、宽、高的和较小时,包装纸箱的表面积较小。这个结论与重叠部分面积较大时,包装纸箱的表面积较小实质上是一致的。因为当其重叠部分的面积较大时,被重叠的所有棱长的和也较大。其余的棱长的和就较小。)
说明:实验的结论不要灌输给学生,每个探索活动都是让学生发挥主体,教师一旁引导即可。
(七)解决情境中问题
设计30个橡皮块的包装纸箱,使纸箱所用材料尽可能少。比较你所列出的方案,由上述三个活动归纳出的结论仍成立吗?(小组合作,记录,汇报)
说明:数量较多,学生摆放方案的寻找有些困难。引导学生先“想”后“做“,将30进行因数分解,30=1×3×10=2×3×5,把其中的一个因数作为层数,另两个因数的积作为每层的块数,这样可以的带如下预设方案:摆10层,每层3块;摆5层,每层6块;摆3层,每层10块;摆2层,每层15块等方案,再结合摆成的长方体的长、宽、高的和较小等因素,就可以较为迅速地找到所需要的方案。
(用探索过的结论解决情境中的问题显得简单多了。学生给出几个主要方案,如上图所示。其中方案1,2的表面积其实是一样的,方案3的表面积更小)
(八)小结
通过本次实验活动,你有哪些感受?
(主要感受:①运用数学中的转化或化归思想,将包装纸箱用料最省的问题转化为求拼成的长方体的表面积最小;②解决较多数量的问题时,往往先列举,再归纳,找出数学规律③学会从生活中的问题抽象出数学模型,会求长方体的表面积④长方体的表面积与棱长之和的关系,棱长和较小时,表面积较小)
(九)课后拓展
1、市场上某种型号的肥皂,它的长、宽、高分别是16cm、6cm、3cm,一箱这种肥皂计30块。请你为肥皂厂设计一种包装纸箱,使该纸箱所用材料尽可能少。
2、去超市调查各种货物的包装,思考其包装的理由,并向工作人员咨询。看自己能否提出更好的包装方案。(设计意图:一是课堂的延伸,强化巩固训练;二是培养学生的交际和思维能力。)
3、请将你的探究经验、活动感受和发现撰写成数学小论文。
板书设计:
设计包装纸箱 ------用料最省方案
设计包装纸箱(生用)
【实验目的】
1.经历“从实际问题抽象出数学问题、建立数学模型、综合运用已有知识解决问题”的过程,
2.通过观察、操作、计算、比较、猜想等活动,提升数学活动的价值,增强数学活动经验
3.在探索活动过程中,体会从特殊到一般、转化的数学思想。
【实验准备】
制作长3 cm、宽2 cm、高1cm的长方体若干个,计算器若干个.
【实验内容和步骤】
1.当包装纸箱装2件上述相同尺寸的产品时,哪种方案所用材料较少?(不考虑包装纸接口重叠部分)
包装纸箱外观尺寸
表面积/cm2 拼法
方案1:
方案2:
方案3:
2.当包装纸箱装3件相同的产品时,哪种方案所用材料较少?
包装纸箱外观尺寸
表面积/cm2 拼法
方案1:
方案2:
方案3:
……
3.当包装纸箱装6件相同的产品时,哪种方案所用材料较少?
包装纸箱外观尺寸
表面积/cm2 拼法
方案1:
方案2:
方案3:
……
4.当包装纸箱装30件相同的产品时,哪种方案所用材料较少?
包装纸箱外观尺寸
表面积/cm2 拼法
方案1:
方案2:
方案3:
……
【自我评价】
1.在活动操作中,各小组都设计了多种不同的方案.在这些方案中,比较好的方案有哪些?它有怎样的特点?
2.参加本次活动,你有哪些收获和体会?
【思考质疑】
操作中的问题与思考 教师批阅意见
【实验成绩】
批阅教师
年 月 日
7
活动目的:
1.经历“从实际问题抽象出数学问题、建立数学模型、综合运用已有知识解决问题”的过程,
2.通过观察、操作、计算、比较、猜想等活动,提升数学活动的价值,增强数学活动经验
3.在探索活动过程中,体会从特殊到一般、转化的数学思想。
活动重点:
1.经历实际问题数学化——建立数学模型——解决问题的过程.
2.丰富空间观念,发展空间想象能力.
活动难点:对用料最省问题的探讨
活动时间:45—50分钟
活动方式:自主探索与小组合作结合
预备知识:长方体的棱长与表面积的关系
活动准备:
长方体模型(长、宽、高分别为3cm、2cm、1cm)(学生课前制作好;每个同学准备6个或者以小组为单位,每组共制作30个)
主要过程:
(一)预习自学
1、已知某个长方体的长、宽、高分别为3cm、2cm、1cm ,若想用包装纸进行包装(不考虑包装纸接口重叠部分),则包装纸至少为多大?(说明:本节数学活动都不考虑包装纸接口重叠部分。下面不再提醒。)
(熟练进行长方体的表面积计算,为下面的活动铺垫)
2、若上述长方体的个数为2,请你设计一种包装纸箱包装,使该纸箱所用材料尽可能少,则包装纸至少为多大?(设计意图:当包装多个长方体物品时,学生容易感知不同的摆放方案,所形成的大长方体棱长有长有短,从而表面积有大小,包装纸材料可以尽可能少,激发学生动手操作并记录数据进行比较的兴趣)
(预习自学环节可以设计到活动学案中,让学生课前完成。课堂上,在问题情境探索的开始部分,引导学生意识到要解决30个相同尺寸的长方体包装纸箱如何设计用料最省的问题,可以先列举出当数量是1,2个时,是怎样设计的,适时汇报课前预习的情况。)
(二)创设情境,引入课题
1.展示一组包装箱(袋),提问:厂家在设计产品的包装箱时,要考虑哪些因素?
(学生可能从形状、材料、美观、成本,有创意、接缝处卡纸的设计等方面回答问题。)
2.形状一般以长方体居多,材料以纸质较多,注重环保,并且我们总希望能利用有限的资源创造出尽可能大的收益。比如考虑到制作成本,厂家会考虑怎样用料较省。
3.现在有30个长、宽、高分别为3cm、2cm、1cm的橡皮块。请你帮厂家设计一种包装纸箱包装,使该纸箱所用材料尽可能少。(说明:橡皮块用课前制作好的长方体代替)
教师点拨:橡皮块类似数学中的模型长方体,一个橡皮块包装材料至少为多少呢?
生回答,与此同时起到复习长方体表面积的计算方法的作用。长方体的表面积等于2×(长×宽+长×高+宽×高)。
点拨:解决数量多的一类问题时,我们通常先列举,再归纳,比如设计两个橡皮块的包装纸,怎样用料最省?
(三)活动1:个数较少情形1——长方体的个数是2
观察操作:自主探索,在表格里填写设计方案,个别展示,回答问题。
(课前学生自学过,可以快速给出拼法示意图,并能计算出长方体的表面积。)
计算比较:我们发现,“计算包装纸的最小面积”的问题实际上可以转化为“计算拼成的大长方体的表面积”问题来解决。
猜想结论:可以发现,如果相同长方体橡皮块的数量一定,当其重叠部分的面积较大时,包装纸箱的表面积较小。
(四)活动2:个数较少情形2——长方体的个数是3
问题1:它们拼成多少种不同的拼接方式?
(学生容易给出3种拼法,将3×2的面重合,3×1的面重合,2×1的面重合。通过计算,得出用料较省的拼法是将3×2的面重合。
教师引导学生说出拼的方式,其实是原来的小长方体的长、宽、高分别扩大了3倍。
问题2:小明同学的拼接方式中有这样一种情形:
2个小长方体在下面,一个在上面,拼接了2层。对此,你有何看法?
(学生通过操作,计算,比较,发现此时的表面积比较大,不是较省的方案。)
问题3:通过上面的探索,我们发现:要想包装纸尽可能少,那么这些小长方体应该拼接成什么形状?(长方体)
问题4:是否还有其他的拼法?如图。
通过计算,发现这样的表面积跟之前的最小方案表面积一样。
猜想结论:同样地,观察示意图,可以发现,如果相同长方体橡皮块的数量一定,当其重叠部分的面积较大时,包装纸箱的表面积较小。
(五)活动3:个数较少的情形3——长方体的个数是6
问题1:有6个这样尺寸的橡皮块,你能将它们拼成多少种不同的长方体?
问题2:你能计算出它们的表面积吗?哪种拼法的表面积最小?
活动方式:以小组合作的形式,组内讨论,一人负责记录,一人汇报方案。
教师注意引导学生想出拼的方式其实是将长,宽,高扩大一定的倍数。而倍数的积就是6。
问题3:之前的猜想仍成立吗?
(六)讨论与交流
: 问题1:通过上述几个活动,你知道怎样拼接小长方体才能使拼成的大长方体的表面积最小?
(同样地,活动1,2的结论是成立的。如果相同长方体橡皮块的数量一定,当其重叠部分的面积较大时,包装纸箱的表面积较小。)
问题2:观察列出的表格,在包装纸箱外观尺寸中,你还能发现长、宽、高的和与表面积有什么关系?
(可以发现:在包装纸箱外观尺寸中,当长、宽、高的和较小时,包装纸箱的表面积较小。这个结论与重叠部分面积较大时,包装纸箱的表面积较小实质上是一致的。因为当其重叠部分的面积较大时,被重叠的所有棱长的和也较大。其余的棱长的和就较小。)
说明:实验的结论不要灌输给学生,每个探索活动都是让学生发挥主体,教师一旁引导即可。
(七)解决情境中问题
设计30个橡皮块的包装纸箱,使纸箱所用材料尽可能少。比较你所列出的方案,由上述三个活动归纳出的结论仍成立吗?(小组合作,记录,汇报)
说明:数量较多,学生摆放方案的寻找有些困难。引导学生先“想”后“做“,将30进行因数分解,30=1×3×10=2×3×5,把其中的一个因数作为层数,另两个因数的积作为每层的块数,这样可以的带如下预设方案:摆10层,每层3块;摆5层,每层6块;摆3层,每层10块;摆2层,每层15块等方案,再结合摆成的长方体的长、宽、高的和较小等因素,就可以较为迅速地找到所需要的方案。
(用探索过的结论解决情境中的问题显得简单多了。学生给出几个主要方案,如上图所示。其中方案1,2的表面积其实是一样的,方案3的表面积更小)
(八)小结
通过本次实验活动,你有哪些感受?
(主要感受:①运用数学中的转化或化归思想,将包装纸箱用料最省的问题转化为求拼成的长方体的表面积最小;②解决较多数量的问题时,往往先列举,再归纳,找出数学规律③学会从生活中的问题抽象出数学模型,会求长方体的表面积④长方体的表面积与棱长之和的关系,棱长和较小时,表面积较小)
(九)课后拓展
1、市场上某种型号的肥皂,它的长、宽、高分别是16cm、6cm、3cm,一箱这种肥皂计30块。请你为肥皂厂设计一种包装纸箱,使该纸箱所用材料尽可能少。
2、去超市调查各种货物的包装,思考其包装的理由,并向工作人员咨询。看自己能否提出更好的包装方案。(设计意图:一是课堂的延伸,强化巩固训练;二是培养学生的交际和思维能力。)
3、请将你的探究经验、活动感受和发现撰写成数学小论文。
板书设计:
设计包装纸箱 ------用料最省方案
设计包装纸箱(生用)
【实验目的】
1.经历“从实际问题抽象出数学问题、建立数学模型、综合运用已有知识解决问题”的过程,
2.通过观察、操作、计算、比较、猜想等活动,提升数学活动的价值,增强数学活动经验
3.在探索活动过程中,体会从特殊到一般、转化的数学思想。
【实验准备】
制作长3 cm、宽2 cm、高1cm的长方体若干个,计算器若干个.
【实验内容和步骤】
1.当包装纸箱装2件上述相同尺寸的产品时,哪种方案所用材料较少?(不考虑包装纸接口重叠部分)
包装纸箱外观尺寸
表面积/cm2 拼法
方案1:
方案2:
方案3:
2.当包装纸箱装3件相同的产品时,哪种方案所用材料较少?
包装纸箱外观尺寸
表面积/cm2 拼法
方案1:
方案2:
方案3:
……
3.当包装纸箱装6件相同的产品时,哪种方案所用材料较少?
包装纸箱外观尺寸
表面积/cm2 拼法
方案1:
方案2:
方案3:
……
4.当包装纸箱装30件相同的产品时,哪种方案所用材料较少?
包装纸箱外观尺寸
表面积/cm2 拼法
方案1:
方案2:
方案3:
……
【自我评价】
1.在活动操作中,各小组都设计了多种不同的方案.在这些方案中,比较好的方案有哪些?它有怎样的特点?
2.参加本次活动,你有哪些收获和体会?
【思考质疑】
操作中的问题与思考 教师批阅意见
【实验成绩】
批阅教师
年 月 日
7
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
