苏科版七年级上册数学 6.5垂直 教案

§6.5垂直
教学设计
教材所处地位分析
教学分析
本节在苏科版在七上第六章平面图形的认识（一）第5节垂直第一课时，是在学行后学习的。在人教版是在七下第五章相交线与平行线第1节第二课时，是在学习了相交线后学习的。
本节课是初中数学数形结合的起始内容，对后期的几何推理有着非常重要的影响，需要让学生认识垂直、表示垂直、理解垂直、并初步运用数形结合思想进行几何推理，并需要学生会找垂直、会折垂直、会画垂直，会运用垂直相关的知识。
教学任务分析
教学目标
1.认识垂直，并会用符号表示，感受数形结合的数学思想。
2.会用三角尺等工具画垂线，在操作过程中探索垂线的基本事实。
教学重点
认识垂直，并用符号表示，会过一点画已知直线的垂线，理解垂线的基本事实。
教学难点
运用垂直定义进行几何推理，初步感受数形结合思想。
教学流程安排
教学流程图
教学内容和目的
板块一
温故知新
板块二
操作与实践
板块三
开拓思维
板块四
课堂小结
由平面内两直线的位置关系引出平行与相交，并进一步研究相交的特殊情况（垂直），接着探究垂直定义。
垂直的定义中的数与形，感受数形结合思想。
通过找、折、画，进一步理解垂直的定义，并通过画垂线得到基本事实。
回顾本课所学，形成体系。
教学过程设计
问题与情境
师生行为
设计意图
板块一
温故知新
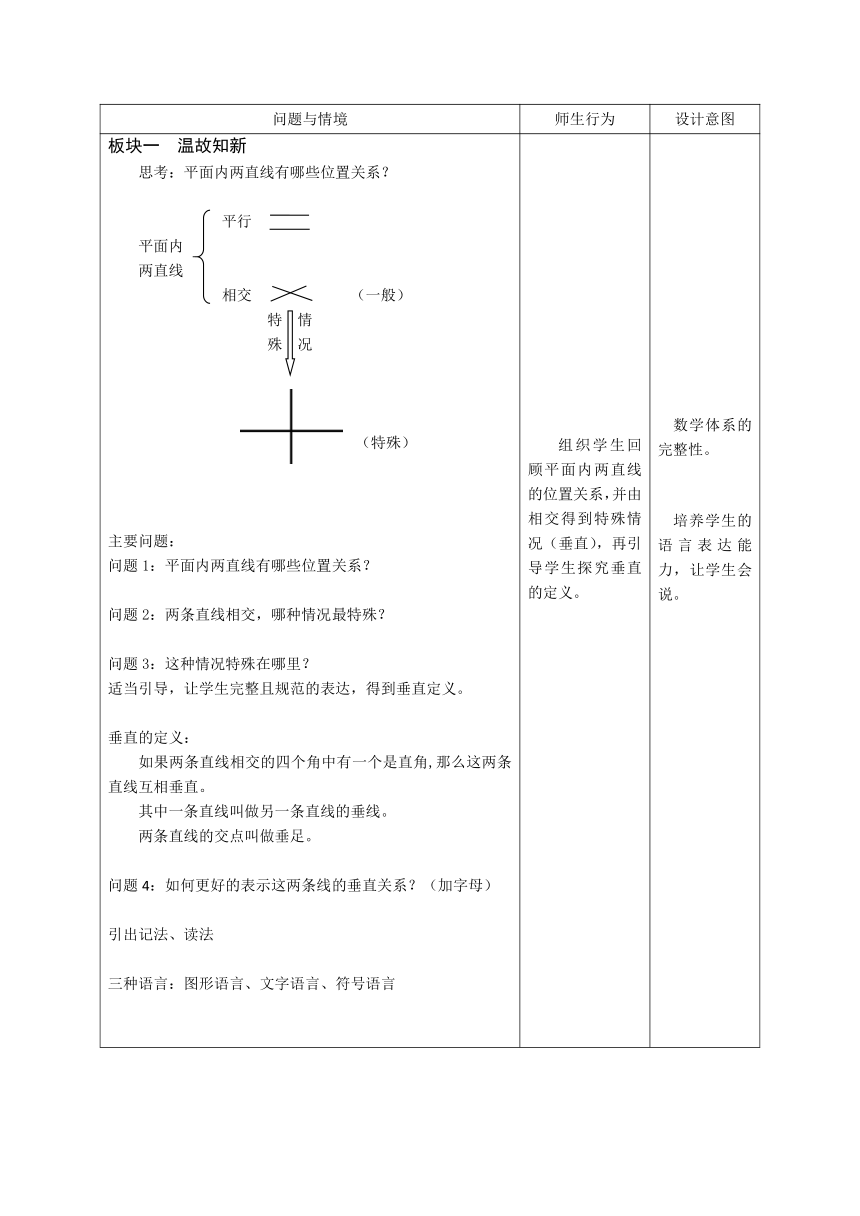
思考：平面内两直线有哪些位置关系？
平行
平面内
两直线
相交
（一般）
特
情
殊
况
（特殊）
主要问题：
问题1：平面内两直线有哪些位置关系？
问题2：两条直线相交，哪种情况最特殊？
问题3：这种情况特殊在哪里？
适当引导，让学生完整且规范的表达，得到垂直定义。
垂直的定义：
如果两条直线相交的四个角中有一个是直角,那么这两条直线互相垂直。
其中一条直线叫做另一条直线的垂线。
两条直线的交点叫做垂足。
问题4：如何更好的表示这两条线的垂直关系？（加字母）
引出记法、读法
三种语言：图形语言、文字语言、符号语言
组织学生回顾平面内两直线的位置关系，并由相交得到特殊情况（垂直），再引导学生探究垂直的定义。
数学体系的完整性。
培养学生的语言表达能力，让学生会说。
板块二
数与形
主要问题：
问题1：在本节课的学习中，有两个非常重要的元素——数与形，关于数，我们知道什么？关于形，我们又知道什么？
问题2：怎样由数得到形，怎样由形得到数？
【数与形】
∠BOC=90°
AB⊥CD
【数
形】
【形
数】
因为∠BOC=90°（已知）
因为AB⊥CD（已知）
所以AB⊥CD（垂直的定义）
所以∠BOC=90°（垂直的定义）
数形结合的思想
【例题】如图,
直线AB、CD相交于点O,
∠EOD=145°,∠1=55°,
判断直线AB与OE的位置关系，并说明理由.
变式：如图,
直线AB、CD相交于点O,
OE⊥AB,
∠1=55°,
求∠EOD的度数.
板块三
操作与思考
活动一
“找”
你能在生活中找到互相垂直的线吗？
活动二
“折”
你能用纸折出两条互相垂直的折痕吗？
活动三
“画”
①你能画直线l的垂线吗？
②已知直线l，请添加一个点P，并过点P画l的垂线。
备用图：
基本事实：在同一平面内，过一点_______
直线与已知直线垂直。
【变式】
如图，请你过点P画出线段AB或射线AB的垂线。
注：画一条线段或者射线的垂线，就是画它们所在直线的垂线。
板块四
课堂小结
通过本节课的学习，你学到了什么？并思考学习的一般套路
让学生理解如何得到垂直，由垂直又能得到什么？感受数形结合的思想。
教师让学生找出生活中的互相垂直的线，并说明理由，强化垂直定义。
教师让学生上台展示怎么折出的互相垂直的折痕，并说明理由，强化垂直定义。
教师让学生画垂线，探究垂线的基本事实。
教师让学生回顾本节课所学内容。
提高学生的理解能力、几何语言表达能力，建立“符号”感。
让学生用数学的眼观观察生活，动手创造，并画出垂线，有助于让学生加深对垂直的认识。并由此探究出垂线的基本事实。
回顾本课所学，形成体系。
教学设计说明
板块一：温故知新
数学学习要成体系，要完整，逻辑性要强，不能是碎片式的，所以本节课从平面内两直线的位置关系开始，先分类，再从一般到特殊，进一步研究这种特殊情况（垂直）。
板块二：数与形
本节课是数形结合起始内容，对后期的几何学习有着深远影响，在本节课一定要让学生理解垂直定义中数与形之间的联系，为了后期的几何学习做好基础。
板块三：操作与思考
对垂直的认识要多角度多样化的，这样才能更深刻的认识和理解垂直，所以让学生找、折、画，再变式，并在过程中探究出垂线的基本事实。
板块四：课堂小结
回顾整节课，形成系统，对垂直有一个更为全面的认识。