高一数学必修3(人教版)课后强化训练(含详解):第三章综合能力检测
文档属性
| 名称 | 高一数学必修3(人教版)课后强化训练(含详解):第三章综合能力检测 |  | |
| 格式 | zip | ||
| 文件大小 | 60.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-17 17:22:16 | ||
图片预览



文档简介
第三章综合能力检测
时间120分钟,满分150分。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)
1.老师为研究男女同学数学学习的差异情况,对某班50名同学(其中男同学30名,女同学20名)采取分层抽样的方法,抽取一个样本容量为10的样本进行研究,求女同学甲被抽到的概率为( )
A. B.
C. D.
[答案] C
[解析] 因为在分层抽样中,任何个体被抽取的概率均相等,所以某女同学甲被抽到的概率为P==,故应选C.
2.有分别写着数字1到120的120张卡片,从中取出1张,这张卡片上的数字是2的倍数或是3的倍数的概率是( )
A. B.
C. D.
[答案] D
[解析] 2的倍数有60个,3的倍数有40个,6的倍数有20个,∴P==.
3.在区间(10,20]内的所有实数中随机取一个实数a,则这个实数a<13的概率是( )
A. B.
C. D.
[答案] C
[解析] 长度型几何概型,概率为.
4.在200个产品中,一等品有60个,二等品有120个,三等品有20个,用分层抽样的方法抽取一个容量20的样本,则二等品中A被抽取到的概率( )
A.等于 B.等于
C.等于 D.不确定
[答案] B
[解析] 每一个个体被抽到的概率都相等,等于
=.
5.一个正四面体的玩具,各面分别标有1,2,3,4中的一个数字,甲、乙两同学玩游戏,每人抛掷一次,朝下一面的数字和为奇数甲胜,否则乙胜,则甲胜的概率为( )
A. B.
C. D.
[答案] B
[解析] 用(x,y)表示第一次抛掷朝下面的数字为x,第二次抛掷朝下一面的数字为y,则x,y的所有可能结果如表
第二次第一次 1 2 3 4
1 (1,1) (1,2) (1,3) (1,4)
2 (2,1) (2,2) (2,3) (2,4)
3 (3,1) (3,2) (3,3) (3,4)
4 (4,1) (4,2) (4,3) (4,4)
共有基本事件16个,其中和为奇数的基本事件有(1,2),(1,4),(2,1),(2,3),(3,2),(3,4),(4,1),(4,3),∴所求概率P==.
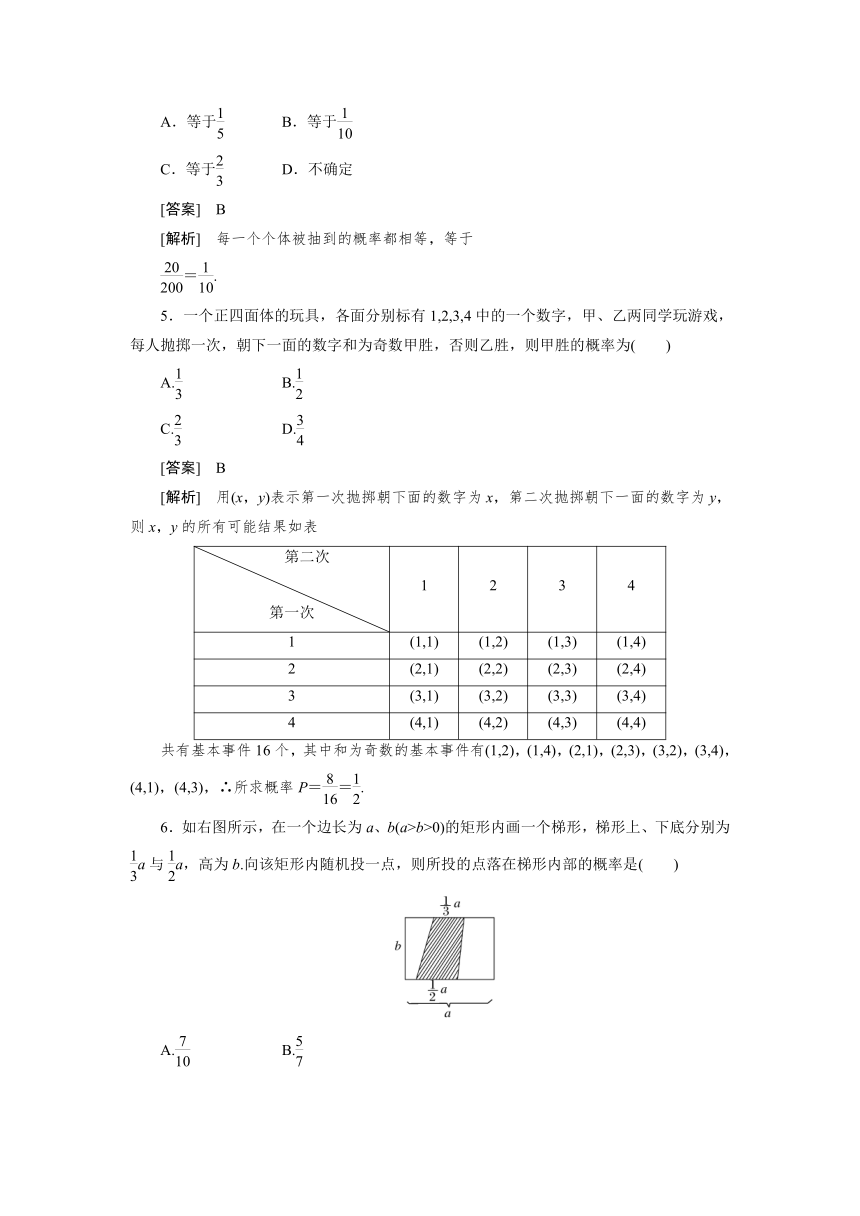
6.如右图所示,在一个边长为a、b(a>b>0)的矩形内画一个梯形,梯形上、下底分别为a与a,高为b.向该矩形内随机投一点,则所投的点落在梯形内部的概率是( )
A. B.
C. D.
[答案] C
[解析] 由几何概型知
P==.
7.掷两颗骰子,事件“点数之和为6”的概率是( )
A. B.
C. D.
[答案] C
[解析] 掷两颗骰子,每颗骰子有6种可能结果,所以共有6×6=36个基本事件,这些事件出现的可能性是相同的;事件“点数之和为6”包括的基本事件有(1,5),(2,4),(3,3),(4,2),(5,1),共有5个.∴P=.故选C.
8.设A为圆周上一点,在圆周上等可能的任取一点与A连接,则弦长超过半径倍的概率是( )
A. B.
C. D.
[答案] B
[解析] 作等腰直角三角形AOC和AMC,B为圆上任一点,则当点B在上运动时,弦长|AB|>R,∴P=.
9.已知正方体ABCD-A1B1C1D1内有一个内切球O,则在正方体ABCD-A1B1C1D1内任取点M,点M在球O内的概率是( )
A. B.
C. D.
[答案] C
[解析] 设正方体棱长为a,则正方体的体积为a3,内切球的体积为π3=πa3,故点M在球O内的概率为=.
10.袋中有红、黄、绿色球各一个,每次任取一个,有放回地抽取三次,球的颜色全相同的概率是( )
A. B.
C. D.
[答案] B
[解析] 有放回地取球三次,共有不同结果33=27种,其中球的颜色全相同的取法有3种,
∴所求概率P==.
11.设l是过点A(1,2)斜率为k的直线,其中k等可能的从集合{-1,-,0,,,,2,3}中取值,则原点到直线l的距离大于1的概率为( )
A. B.
C. D.
[答案] B
[解析] l:y-2=k(x-1),即kx-y-k+2=0,
由题意>1,∴k2-4k+4>1+k2,
∴k<,故当k<时,事件A=“原点到直线l的距离大于1”发生,∴P(A)=.
12.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如下:
根据上图可得这100名学生中体重在[56.5,64.5]的学生人数是( )
A.20 B.30
C.40 D.50
[答案] C
[解析] ∵体重在[56.5,64.5]间的频率为:2(0.03+2×0.05+0.07)=0.4.
∴学生人数为0.4×100=40人.
二、填空题(本大题共4个小题,每小题4分,共16分,把正确答案填在题中横线上)
13.口袋内装有一些大小相同的红球、黄球、白球,从中摸出一个球,摸出红球或白球的概率为0.65,摸出黄球或白球的概率是0.6,那么摸出白球的概率是______.
[答案] 0.25
[解析] 设摸出红球、白球、黄球的事件分别为A、B、C,由条件P(A∪B)=P(A)+P(B)=0.65,
P(B∪C)=P(B)+P(C)=0.6,
又P(A∪B)=1-P(C),∴P(C)=0.35,
∴P(B)=0.25.
14.在边长为2的正△ABC所在平面内,以A为圆心,为半径画一弧,分别交AB、AC于D、E.若在△ABC这一平面区域内任丢一粒豆子,则豆子落在扇形ADE内的概率是________.
[答案]
[解析] 由题意知,△ABC中BC边上的高AO正好为,
∴弧与AB相切,如图.
S扇形=···=,
S△ABC=×2×2×=,
∴P==.
15.随意安排甲、乙、丙三人在3天节日中值班,每人值班1天,甲排在乙之前的概率是________.
[答案]
[解析] 甲、乙、丙三人排在三天中值班,每人1天,故甲在乙前和乙在甲前的机会相等,∴概率为.
16.某汽车站每天均有3辆开往省城济南的分为上、中、下等级的客车,某天袁先生准备在该汽车站乘车前往济南办事,但他不知道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他采取如下策略:先放过第一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆.那么他乘上上等车的概率为________.
[答案]
[解析] 共有6种发车顺序①上、中、下②上、下、中③中、上、下④中、下、上⑤下、中、上⑥下、上、中(其中画横线的表示袁先生所乘的车),所以他乘坐上等车的概率为=.
三、解答题(本大题共6个大题,共74分,解答应写出文字说明,证明过程或演算步骤)
17.(本题满分12分)指出下列事件是必然事件,不可能事件,还是随机事件?
(1)每天早晨,太阳从东方升起;
(2)在标准大气压下,水的温度达到80°C时沸腾;
(3)某地3月4日出现沙尘暴天气;
(4)某寻呼机在一分钟内接到8次寻呼.
[解析] (1)每天早晨,太阳从东方升起是必然现象,所以是必然事件;
(2)因为在标准大气压下,水的温度达到100°C时才可沸腾,所以(2)是不可能事件;
(3)某地出现沙尘暴天气是偶然的,因而在3月4日可能出现沙尘暴天气,也可能是晴天,故该事件是随机事件;
(4)某寻呼机在一分钟内接到的寻呼次数也可能低于8次,还可能高于8次,故该事件亦是随机事件.
[点评] 本例的求解关键在于准确理解几种事件各自的概念,注意判断的前提是在一定条件之下.例如(2),若没有“标准大气压”这一条件,水在80°C时也可能会沸腾.
18.(本题满分12分)某城市有甲、乙两种报纸供居民们订阅,记事件A为“只订甲报”,事件B为“至少订一种报”,事件C为“至多订一种报”,事件D为“不订甲报”,事件E为“一种报也不订”.判断下列每对事件是不是互斥事件;如果是,再判断它们是不是对立事件.
(1)A与C (2)B与E
(3)B与D (4)B与C
(5)C与E
[解析] (1)由于事件C“至多订一种报”中有可能只订甲报,即事件A与事件C有可能同时发生,故A与C不是互斥事件.
(2)事件B“至少订一种报”与事件E“一种报也不订”是不可能同时发生的,故B与E是互斥事件.由于事件B发生可导致事件E一定不发生,且事件E发生会导致事件B一定不发生,故B与E还是对立事件.
(3)事件B“至少订一种报”中有可能只订乙报,即有可能不订甲报,即事件B发生,事件D也可能发生,故B与D不互斥.
(4)事件B“至少订一种报”中有这些可能:“只订甲报”、“只订乙报”、“订甲、乙两种报”,事件C“至多订一种报”中有这些可能:“什么也不订”、“只订甲报”、“只订乙报”,由于这两个事件可能同时发生,故B与C不是互斥事件.
(5)由(4)的分析,事件E“一种报也不订”只是事件C的一种可能,故事件C与事件E有可能同时发生,故C与E不互斥.
[点评] 由对立事件的定义可知,对立事件首先是互斥事件,并且其中一个一定要发生,因此两个对立事件一定是互斥事件,但两个互斥事件却不一定是对立事件.解题时一定要搞清两种事件的关系.
19.(本题满分12分)任选一个三位数,求恰好是100的倍数的概率.
[解析] 三位数共有900个,其中是100的倍数的三位数有9个,
∴所求概率为P==0.01.
20.(本题满分12分)5张奖券中有2张是中奖的,首先由甲抽一张,然后由乙抽一张,求:
(1)甲中奖的概率P(A).
(2)甲、乙都中奖的概率P(B).
(3)只有乙中奖的概率P(C).
(4)乙中奖的概率P(D).
[解析] 将5张奖券编号为1,2,3,4,5,其中4、5为中奖奖券,用(x,y)表示甲抽到号码x,乙抽到号码y,则所有可能抽法构成集合Ω={(1,2),(1,3),(1,4),(1,5),(2,1),(2,3),(2,4),(2,5),(3,1),(3,2),(3,4),(3,5),(4,1),(4,2),(4,3),(4,5),(5,1),(5,2),(5,3),(5,4)}.
(1)甲中奖包含8个基本事件,∴P(A)==.
(2)甲、乙都中奖包含2个基本事件,
∴P(B)==.
(3)只有乙中奖包含6个基本事件,∴P(C)==.
(4)乙中奖包含8个基本事件,∴P(D)==.
21.(本题满分12分)一个口袋里有2个红球和4个黄球,从中随机地连取3个球,每次取一个,记事件A=“恰有一个红球”,事件B=“第3个是红球”.求
(1)不放回时,事件A,B的概率.
(2)每次抽后放回时,A,B的概率.
[解析] (1)由不放回抽样可知,第一次从6个球中抽一个,第二次只能从5个球中取一个,第三次从4个球中取一个,基本事件共6×5×4=120个,又事件A中含有基本事件3×2×4×3=72个,(第一个是红球,则第2、3个是黄球,取法有2×4×3种,第2个是红球和第3个是红球取法一样多)
∴P(A)==.
第3次抽到红球对前两次没有什么要求,因为红球数占总球数的,在每一次抽到都是随机地等可能事件,∴P(B)=.
(2)由放回抽样知,每次都是从6个球中取一个,有取法63=216种,事件A包含基本事件3×2×4×4=96种.
∴P(A)==.
第三次抽到红球包括B1={红,黄,红},B2={黄,黄,红},B3={黄,红,红}三种两两互斥的情形,P(B1)==.P(B2)==,P(B3)==,
∴P(B)=P(B1)+P(B2)+P(B3)
=++=.
[点评] (1)求基本事件总数可用平面直角坐标系中的点或空间直角坐标系中的点来直观数出,也可以直接用列举法.
(2)第三次抽到红球的概率只与红球所占比例有关与第n次抽样无关,也与有无放回抽样无关,故求某次取到某种样品的抽样问题,也可直接用比例算法求得.
22.(本题满分14分)设集合A={x|<0},若p、q∈A,求方程x2+2px-q2+1=0有两实根的概率.
[解析] A={x|-3若使方程有两实根,应有
Δ=(2p)2-4(-q2+1)=4p2+4q2-4≥0,
∴p2+q2≥1,
∴点(p,q)应落在圆x2+y2=1的外部,由几何概型的定义知,所求概率为P==.
时间120分钟,满分150分。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)
1.老师为研究男女同学数学学习的差异情况,对某班50名同学(其中男同学30名,女同学20名)采取分层抽样的方法,抽取一个样本容量为10的样本进行研究,求女同学甲被抽到的概率为( )
A. B.
C. D.
[答案] C
[解析] 因为在分层抽样中,任何个体被抽取的概率均相等,所以某女同学甲被抽到的概率为P==,故应选C.
2.有分别写着数字1到120的120张卡片,从中取出1张,这张卡片上的数字是2的倍数或是3的倍数的概率是( )
A. B.
C. D.
[答案] D
[解析] 2的倍数有60个,3的倍数有40个,6的倍数有20个,∴P==.
3.在区间(10,20]内的所有实数中随机取一个实数a,则这个实数a<13的概率是( )
A. B.
C. D.
[答案] C
[解析] 长度型几何概型,概率为.
4.在200个产品中,一等品有60个,二等品有120个,三等品有20个,用分层抽样的方法抽取一个容量20的样本,则二等品中A被抽取到的概率( )
A.等于 B.等于
C.等于 D.不确定
[答案] B
[解析] 每一个个体被抽到的概率都相等,等于
=.
5.一个正四面体的玩具,各面分别标有1,2,3,4中的一个数字,甲、乙两同学玩游戏,每人抛掷一次,朝下一面的数字和为奇数甲胜,否则乙胜,则甲胜的概率为( )
A. B.
C. D.
[答案] B
[解析] 用(x,y)表示第一次抛掷朝下面的数字为x,第二次抛掷朝下一面的数字为y,则x,y的所有可能结果如表
第二次第一次 1 2 3 4
1 (1,1) (1,2) (1,3) (1,4)
2 (2,1) (2,2) (2,3) (2,4)
3 (3,1) (3,2) (3,3) (3,4)
4 (4,1) (4,2) (4,3) (4,4)
共有基本事件16个,其中和为奇数的基本事件有(1,2),(1,4),(2,1),(2,3),(3,2),(3,4),(4,1),(4,3),∴所求概率P==.
6.如右图所示,在一个边长为a、b(a>b>0)的矩形内画一个梯形,梯形上、下底分别为a与a,高为b.向该矩形内随机投一点,则所投的点落在梯形内部的概率是( )
A. B.
C. D.
[答案] C
[解析] 由几何概型知
P==.
7.掷两颗骰子,事件“点数之和为6”的概率是( )
A. B.
C. D.
[答案] C
[解析] 掷两颗骰子,每颗骰子有6种可能结果,所以共有6×6=36个基本事件,这些事件出现的可能性是相同的;事件“点数之和为6”包括的基本事件有(1,5),(2,4),(3,3),(4,2),(5,1),共有5个.∴P=.故选C.
8.设A为圆周上一点,在圆周上等可能的任取一点与A连接,则弦长超过半径倍的概率是( )
A. B.
C. D.
[答案] B
[解析] 作等腰直角三角形AOC和AMC,B为圆上任一点,则当点B在上运动时,弦长|AB|>R,∴P=.
9.已知正方体ABCD-A1B1C1D1内有一个内切球O,则在正方体ABCD-A1B1C1D1内任取点M,点M在球O内的概率是( )
A. B.
C. D.
[答案] C
[解析] 设正方体棱长为a,则正方体的体积为a3,内切球的体积为π3=πa3,故点M在球O内的概率为=.
10.袋中有红、黄、绿色球各一个,每次任取一个,有放回地抽取三次,球的颜色全相同的概率是( )
A. B.
C. D.
[答案] B
[解析] 有放回地取球三次,共有不同结果33=27种,其中球的颜色全相同的取法有3种,
∴所求概率P==.
11.设l是过点A(1,2)斜率为k的直线,其中k等可能的从集合{-1,-,0,,,,2,3}中取值,则原点到直线l的距离大于1的概率为( )
A. B.
C. D.
[答案] B
[解析] l:y-2=k(x-1),即kx-y-k+2=0,
由题意>1,∴k2-4k+4>1+k2,
∴k<,故当k<时,事件A=“原点到直线l的距离大于1”发生,∴P(A)=.
12.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如下:
根据上图可得这100名学生中体重在[56.5,64.5]的学生人数是( )
A.20 B.30
C.40 D.50
[答案] C
[解析] ∵体重在[56.5,64.5]间的频率为:2(0.03+2×0.05+0.07)=0.4.
∴学生人数为0.4×100=40人.
二、填空题(本大题共4个小题,每小题4分,共16分,把正确答案填在题中横线上)
13.口袋内装有一些大小相同的红球、黄球、白球,从中摸出一个球,摸出红球或白球的概率为0.65,摸出黄球或白球的概率是0.6,那么摸出白球的概率是______.
[答案] 0.25
[解析] 设摸出红球、白球、黄球的事件分别为A、B、C,由条件P(A∪B)=P(A)+P(B)=0.65,
P(B∪C)=P(B)+P(C)=0.6,
又P(A∪B)=1-P(C),∴P(C)=0.35,
∴P(B)=0.25.
14.在边长为2的正△ABC所在平面内,以A为圆心,为半径画一弧,分别交AB、AC于D、E.若在△ABC这一平面区域内任丢一粒豆子,则豆子落在扇形ADE内的概率是________.
[答案]
[解析] 由题意知,△ABC中BC边上的高AO正好为,
∴弧与AB相切,如图.
S扇形=···=,
S△ABC=×2×2×=,
∴P==.
15.随意安排甲、乙、丙三人在3天节日中值班,每人值班1天,甲排在乙之前的概率是________.
[答案]
[解析] 甲、乙、丙三人排在三天中值班,每人1天,故甲在乙前和乙在甲前的机会相等,∴概率为.
16.某汽车站每天均有3辆开往省城济南的分为上、中、下等级的客车,某天袁先生准备在该汽车站乘车前往济南办事,但他不知道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他采取如下策略:先放过第一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆.那么他乘上上等车的概率为________.
[答案]
[解析] 共有6种发车顺序①上、中、下②上、下、中③中、上、下④中、下、上⑤下、中、上⑥下、上、中(其中画横线的表示袁先生所乘的车),所以他乘坐上等车的概率为=.
三、解答题(本大题共6个大题,共74分,解答应写出文字说明,证明过程或演算步骤)
17.(本题满分12分)指出下列事件是必然事件,不可能事件,还是随机事件?
(1)每天早晨,太阳从东方升起;
(2)在标准大气压下,水的温度达到80°C时沸腾;
(3)某地3月4日出现沙尘暴天气;
(4)某寻呼机在一分钟内接到8次寻呼.
[解析] (1)每天早晨,太阳从东方升起是必然现象,所以是必然事件;
(2)因为在标准大气压下,水的温度达到100°C时才可沸腾,所以(2)是不可能事件;
(3)某地出现沙尘暴天气是偶然的,因而在3月4日可能出现沙尘暴天气,也可能是晴天,故该事件是随机事件;
(4)某寻呼机在一分钟内接到的寻呼次数也可能低于8次,还可能高于8次,故该事件亦是随机事件.
[点评] 本例的求解关键在于准确理解几种事件各自的概念,注意判断的前提是在一定条件之下.例如(2),若没有“标准大气压”这一条件,水在80°C时也可能会沸腾.
18.(本题满分12分)某城市有甲、乙两种报纸供居民们订阅,记事件A为“只订甲报”,事件B为“至少订一种报”,事件C为“至多订一种报”,事件D为“不订甲报”,事件E为“一种报也不订”.判断下列每对事件是不是互斥事件;如果是,再判断它们是不是对立事件.
(1)A与C (2)B与E
(3)B与D (4)B与C
(5)C与E
[解析] (1)由于事件C“至多订一种报”中有可能只订甲报,即事件A与事件C有可能同时发生,故A与C不是互斥事件.
(2)事件B“至少订一种报”与事件E“一种报也不订”是不可能同时发生的,故B与E是互斥事件.由于事件B发生可导致事件E一定不发生,且事件E发生会导致事件B一定不发生,故B与E还是对立事件.
(3)事件B“至少订一种报”中有可能只订乙报,即有可能不订甲报,即事件B发生,事件D也可能发生,故B与D不互斥.
(4)事件B“至少订一种报”中有这些可能:“只订甲报”、“只订乙报”、“订甲、乙两种报”,事件C“至多订一种报”中有这些可能:“什么也不订”、“只订甲报”、“只订乙报”,由于这两个事件可能同时发生,故B与C不是互斥事件.
(5)由(4)的分析,事件E“一种报也不订”只是事件C的一种可能,故事件C与事件E有可能同时发生,故C与E不互斥.
[点评] 由对立事件的定义可知,对立事件首先是互斥事件,并且其中一个一定要发生,因此两个对立事件一定是互斥事件,但两个互斥事件却不一定是对立事件.解题时一定要搞清两种事件的关系.
19.(本题满分12分)任选一个三位数,求恰好是100的倍数的概率.
[解析] 三位数共有900个,其中是100的倍数的三位数有9个,
∴所求概率为P==0.01.
20.(本题满分12分)5张奖券中有2张是中奖的,首先由甲抽一张,然后由乙抽一张,求:
(1)甲中奖的概率P(A).
(2)甲、乙都中奖的概率P(B).
(3)只有乙中奖的概率P(C).
(4)乙中奖的概率P(D).
[解析] 将5张奖券编号为1,2,3,4,5,其中4、5为中奖奖券,用(x,y)表示甲抽到号码x,乙抽到号码y,则所有可能抽法构成集合Ω={(1,2),(1,3),(1,4),(1,5),(2,1),(2,3),(2,4),(2,5),(3,1),(3,2),(3,4),(3,5),(4,1),(4,2),(4,3),(4,5),(5,1),(5,2),(5,3),(5,4)}.
(1)甲中奖包含8个基本事件,∴P(A)==.
(2)甲、乙都中奖包含2个基本事件,
∴P(B)==.
(3)只有乙中奖包含6个基本事件,∴P(C)==.
(4)乙中奖包含8个基本事件,∴P(D)==.
21.(本题满分12分)一个口袋里有2个红球和4个黄球,从中随机地连取3个球,每次取一个,记事件A=“恰有一个红球”,事件B=“第3个是红球”.求
(1)不放回时,事件A,B的概率.
(2)每次抽后放回时,A,B的概率.
[解析] (1)由不放回抽样可知,第一次从6个球中抽一个,第二次只能从5个球中取一个,第三次从4个球中取一个,基本事件共6×5×4=120个,又事件A中含有基本事件3×2×4×3=72个,(第一个是红球,则第2、3个是黄球,取法有2×4×3种,第2个是红球和第3个是红球取法一样多)
∴P(A)==.
第3次抽到红球对前两次没有什么要求,因为红球数占总球数的,在每一次抽到都是随机地等可能事件,∴P(B)=.
(2)由放回抽样知,每次都是从6个球中取一个,有取法63=216种,事件A包含基本事件3×2×4×4=96种.
∴P(A)==.
第三次抽到红球包括B1={红,黄,红},B2={黄,黄,红},B3={黄,红,红}三种两两互斥的情形,P(B1)==.P(B2)==,P(B3)==,
∴P(B)=P(B1)+P(B2)+P(B3)
=++=.
[点评] (1)求基本事件总数可用平面直角坐标系中的点或空间直角坐标系中的点来直观数出,也可以直接用列举法.
(2)第三次抽到红球的概率只与红球所占比例有关与第n次抽样无关,也与有无放回抽样无关,故求某次取到某种样品的抽样问题,也可直接用比例算法求得.
22.(本题满分14分)设集合A={x|<0},若p、q∈A,求方程x2+2px-q2+1=0有两实根的概率.
[解析] A={x|-3
Δ=(2p)2-4(-q2+1)=4p2+4q2-4≥0,
∴p2+q2≥1,
∴点(p,q)应落在圆x2+y2=1的外部,由几何概型的定义知,所求概率为P==.
