华东师大版 八年级数学上册 13.2.1全等三角形课件(24张PPT)
文档属性
| 名称 | 华东师大版 八年级数学上册 13.2.1全等三角形课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 10:32:08 | ||
图片预览



文档简介
(共24张PPT)
2.1全等三角形
华师版八年级上学期
第13章
《全等三角形》
学而不疑则怠,疑而不探则空
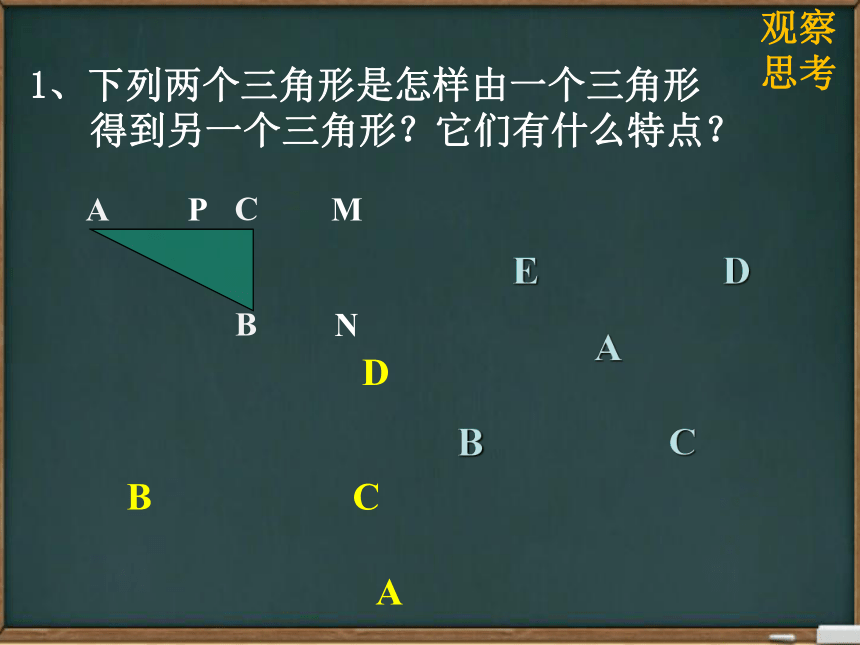
1、下列两个三角形是怎样由一个三角形
得到另一个三角形?它们有什么特点?
B
A
C
N
P
M
A
C
B
D
E
A
C
B
D
观察思考
B
A
C
一个三角形经过平移、旋转、翻折等位移变换后得到另一个三角形。
位置改变,但形状、大小不变。
结论:
N
M
S
O
T
D
C
O
A
B
A
B
C
D
E
F
2、下列各图中的两个三角形是全等形吗?
结论:经过平移、旋转、翻折等位移变换
得到的三角形与原三角形全等。
观察思考
A
B
C
E
D
F
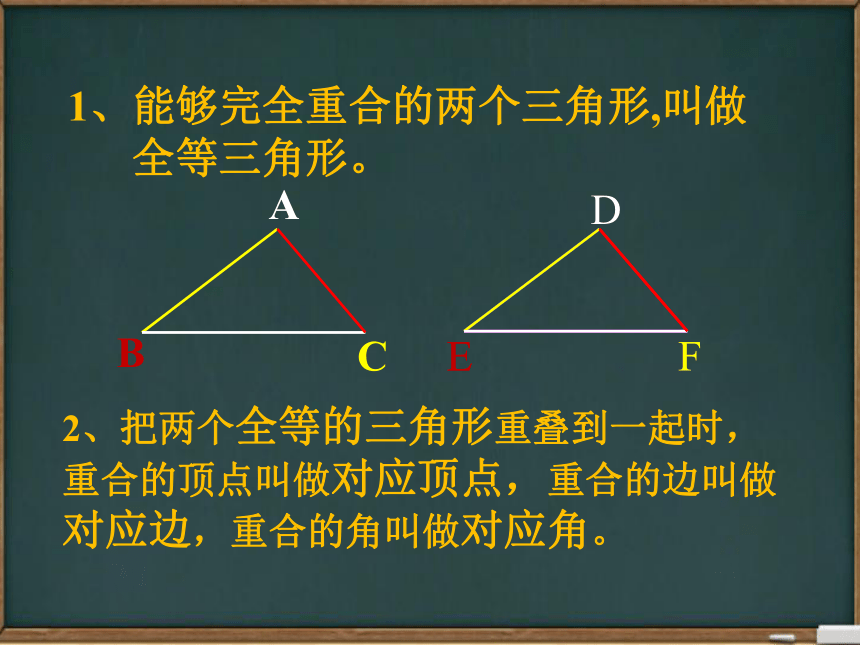
1、能够完全重合的两个三角形,叫做
全等三角形。
E
D
F
2、把两个全等的三角形重叠到一起时,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
归纳
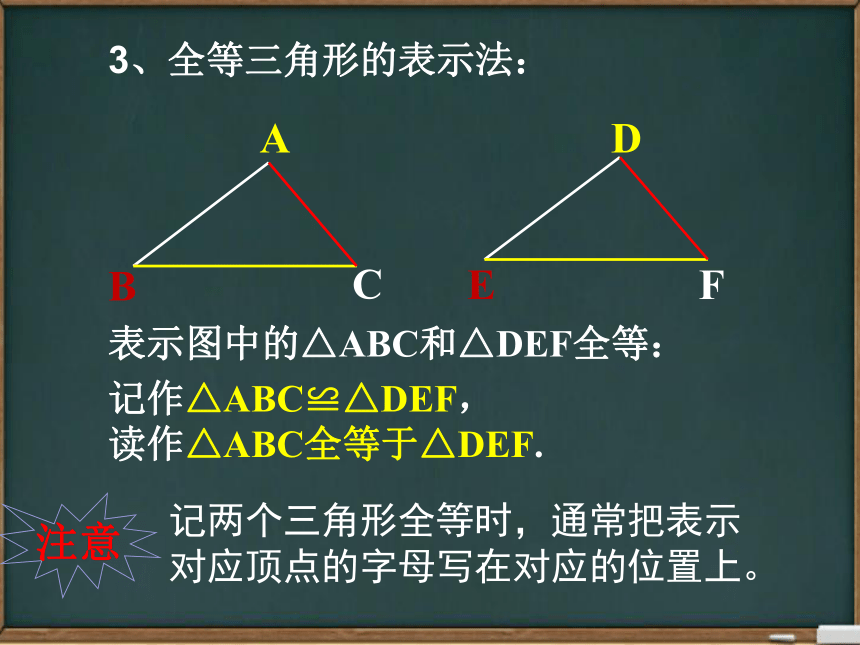
表示图中的△ABC和△DEF全等:
3、全等三角形的表示法:
记作△ABC≌△DEF,
读作△ABC全等于△DEF.
注意
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
A
B
C
E
D
F
S
O
T
D
C
N
M
O
A
B
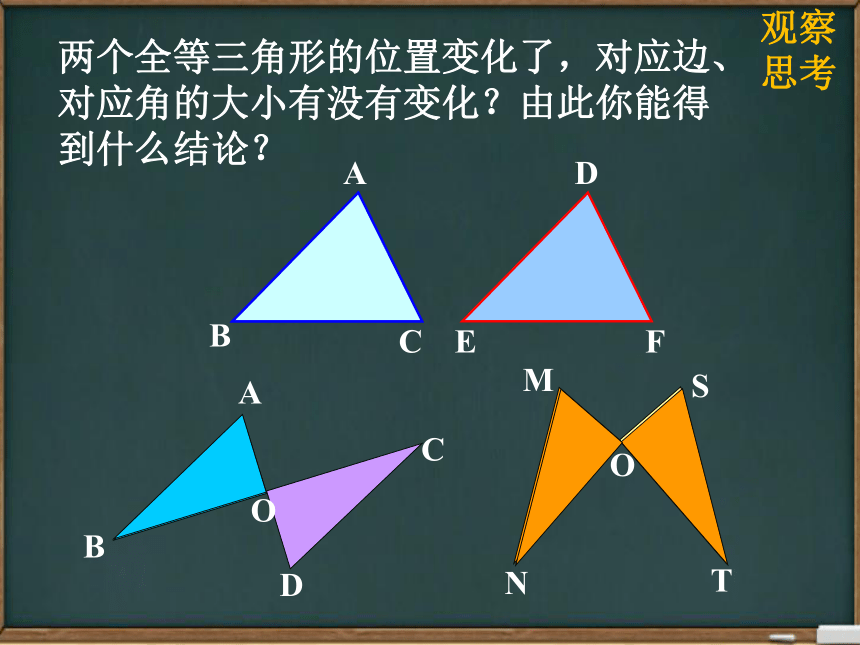
两个全等三角形的位置变化了,对应边、对应角的大小有没有变化?由此你能得到什么结论?
E
A
D
C
B
F
观察思考
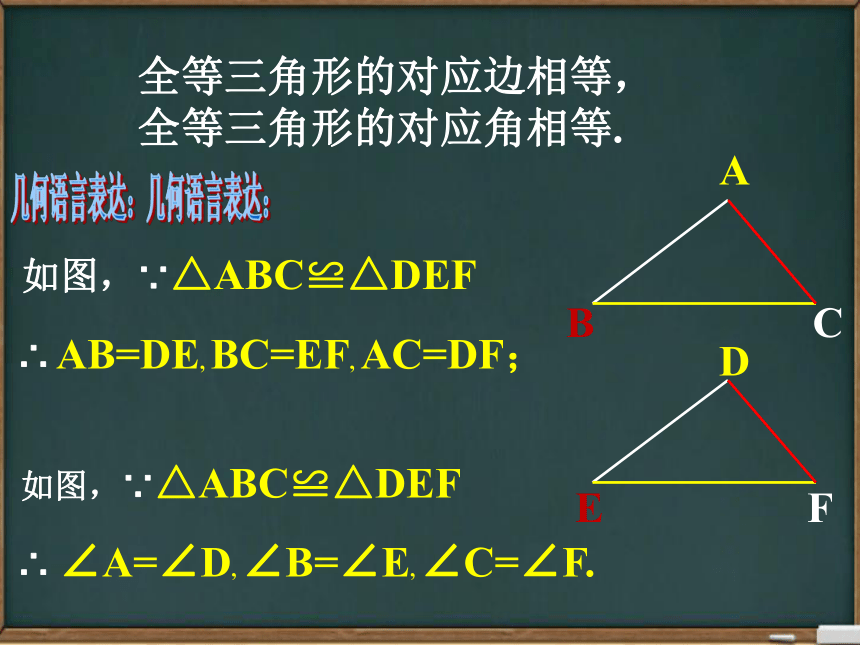
全等三角形的对应边相等,全等三角形的对应角相等.
如图,∵△ABC≌△DEF
∴
AB=DE,
BC=EF,
AC=DF;
几何语言表达:
全等三角形
的性质
如图,∵△ABC≌△DEF
∴
∠A=∠D,
∠B=∠E,
∠C=∠F.
归纳
A
B
C
E
D
F
A
B
C
L
N
M
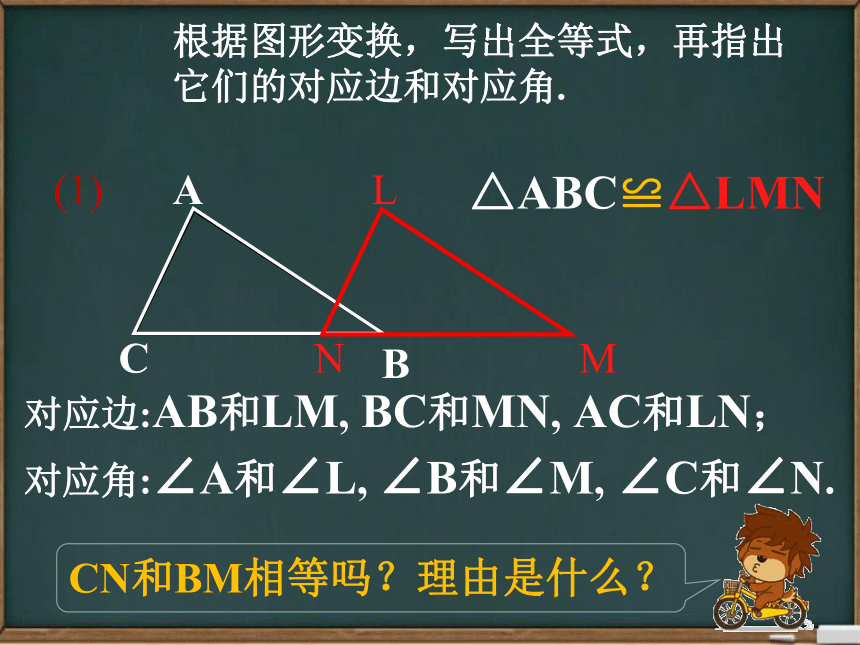
根据图形变换,写出全等式,再指出它们的对应边和对应角.
应用交流
△ABC≌△LMN
对应边:AB和LM,
BC和MN,
AC和LN;
对应角:∠A和∠L,
∠B和∠M,
∠C和∠N.
(1)
CN和BM相等吗?理由是什么?
A
B
C
D
规律一:有公共边的,公共边是对应边.
△ABC≌△ABD
对应边:AB和AB,
BC和BD,
AC和AD;
对应角:∠BAC和∠BAD,
∠ABC和∠ABD,
∠C和∠D.
(2)
应用交流
A
B
C
D
E
△ABC≌△ADE
对应边:AB和AD,
AC和AE,
BC和DE;
对应角:∠ACB和∠AED,
∠B和∠D,
∠BAC和∠DAE.
规律二:有公共角的,公共角是对应角.
(3)
应用交流
A
C
B
D
规律三:有对顶角的,对顶角是对应角.
△AOC≌△BOD
对应边:OA和OB,OC和OD,
AC和BD;
对应角:∠AOC和∠BOD,
∠A和∠B,
∠C和∠D.
O
(4)
应用交流
A
B
C
F
D
E
△ABC≌△DEF
对应边:AB和DE,
AC和DF,
BC和EF;
对应角:∠A和∠D,
∠B和∠E,
∠C和∠F.
规律四:
最长的边是对应边,
最短的边是对应边;
规律五:
最大的角是对应角,
最小的角是对应角.
(5)
应用交流
3.有公共角的,公共角一定是对应角。
4.对应角所对的边是对应边,
对应边所对的角是对应角.
5.在两个全等三角形中
最长边对最长边,最短边对最短边;
最大角对最大角,最小角对最小角。
1.有公共边的,公共边一定是对应边。
2.有对顶角的,对顶角一定是对应角。
规律总结
6.根据书写规范,按对应顶点找对应边(角)。
1、有公共边
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共顶点
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
典型图例
写出下列全等三角形中相等的边和角:
A
B
C
D
课堂练习
△ABD≌△CBD
(1)
AB=CB,
AD=CD,
BD=BD;
∠A=∠C,
∠ABD=∠CBD,
∠ADB=∠CDB.
A
B
C
D
O
(2)
△OAB≌△OCD
OA=OC,
OB=OD,
AB=CD;
∠A=∠C,∠B=∠D,
∠AOB=∠COD.
△ABC≌△ADE
(3)
AB=AD,
AC=AE,
BC=DE;
∠B=∠D,
∠C=∠E,
∠BAC=∠DAE.
(4)
△ADE≌△CBF
A
B
D
C
E
B
F
C
D
A
E
AD=CB,
AE=CF,
DE=BF;
∠A=∠C,
∠ADE=∠CBF,
∠AED=∠CFB.
△ABN≌△ACM
(5)
AB=AC,
AN=AM,
BN=CM;
∠B=∠C,
∠ANB=∠AMC,
∠BAN=∠CAM.
(6)
△AOB≌△DOC
AB=DC,
AO=DO,
BO=CO;
∠A=∠D,
∠AOB=∠DOC,
∠ABO=∠DCO.
A
B
M
N
C
A
B
C
D
O
△ABC≌△DCB
AB=DC,
AC=DB,
BC=CB;
∠A=∠D,
∠ABC=∠DCB,
∠ACB=∠DBC.
1、若△AOC≌△BOD,
则AC=
,∠A=
.
A
B
O
C
D
2、若△ABD≌△ACE,
则BD=
,∠BDA=
.
3、若△ABC≌△CDA,
则AB=
,∠BAC=
.
A
B
C
D
填空:
BD
∠B
CE
∠CEA
CD
∠DCA
A
B
C
D
E
公共点
公共角
公共边
A
D
C
B
A
E
B
D
C
A
B
C
D
E
F
(2)已知△ABC≌△CDA,
则AC边的对应边为
.
(1)已知△ABC≌△ADE,
则∠A的对应角为
.
(3)已知△ABC≌△DEF,
则AB边的对应边为
,
∠C的对应角为
.
CA
∠A
DE
∠F
填一填:
1、如图,已知△AOC≌△BOD,
求证:AC∥BD.
拓展
提高
证明:
∵△AOC≌△BOD,
(已知)
∴∠A=∠B,
(全等三角形的对应角相等)
∴AC∥BD.
(内错角相等,两直线平行)
A
B
D
C
O
2、如图,已知△ABD≌△ACE,且∠C=50?,
∠A=30?,AC=
8,AE
=
5,求∠ADB及DC.
A
E
B
C
D
解:
∵△ABD≌△ACE,
∴∠B=∠C=50°
?
(全等三角形的对应角相等)
∵∠A=30°,
∴∠ADB=180°-∠A-∠B
=100°.
∵△ABD≌△ACE,
∴AD=AE=5.
(全等三角形的对应边相等)
∵AC=
8,
∴DC=AC-AD=3.
5
5
3
3、如图,
△EFG≌△NMH.
(2)如果EF=2.1cm,EH=1.1cm,HN=3.3cm,
求NM、HG的长.
(1)请找出对应边和对应角。
N
M
F
G
E
H
(3)在(2)的条件下,若FG=4cm,
求△NMH的周长.
2.1
1.1
3.3
2.1
2.2
(4)这两个三角形的面积相等吗?
互相重合的角叫做
.
互相重合的边叫做
,
其中:互相重合的顶点叫做
,
2.
叫全等三角形.
1.能够重合的两个图形叫做
。
全等形
4.全等三角形的
和
相等.
对应边
对应角
对应顶点
课堂小结
能够完全重合的两个三角形
3.“全等”用符号“
”来表示,
读作“
”.
对应边
对应角
5.书写全等式时要求把对应字母放在对应
的位置上.
全等于
≌
2.1全等三角形
华师版八年级上学期
第13章
《全等三角形》
学而不疑则怠,疑而不探则空
1、下列两个三角形是怎样由一个三角形
得到另一个三角形?它们有什么特点?
B
A
C
N
P
M
A
C
B
D
E
A
C
B
D
观察思考
B
A
C
一个三角形经过平移、旋转、翻折等位移变换后得到另一个三角形。
位置改变,但形状、大小不变。
结论:
N
M
S
O
T
D
C
O
A
B
A
B
C
D
E
F
2、下列各图中的两个三角形是全等形吗?
结论:经过平移、旋转、翻折等位移变换
得到的三角形与原三角形全等。
观察思考
A
B
C
E
D
F
1、能够完全重合的两个三角形,叫做
全等三角形。
E
D
F
2、把两个全等的三角形重叠到一起时,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
归纳
表示图中的△ABC和△DEF全等:
3、全等三角形的表示法:
记作△ABC≌△DEF,
读作△ABC全等于△DEF.
注意
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
A
B
C
E
D
F
S
O
T
D
C
N
M
O
A
B
两个全等三角形的位置变化了,对应边、对应角的大小有没有变化?由此你能得到什么结论?
E
A
D
C
B
F
观察思考
全等三角形的对应边相等,全等三角形的对应角相等.
如图,∵△ABC≌△DEF
∴
AB=DE,
BC=EF,
AC=DF;
几何语言表达:
全等三角形
的性质
如图,∵△ABC≌△DEF
∴
∠A=∠D,
∠B=∠E,
∠C=∠F.
归纳
A
B
C
E
D
F
A
B
C
L
N
M
根据图形变换,写出全等式,再指出它们的对应边和对应角.
应用交流
△ABC≌△LMN
对应边:AB和LM,
BC和MN,
AC和LN;
对应角:∠A和∠L,
∠B和∠M,
∠C和∠N.
(1)
CN和BM相等吗?理由是什么?
A
B
C
D
规律一:有公共边的,公共边是对应边.
△ABC≌△ABD
对应边:AB和AB,
BC和BD,
AC和AD;
对应角:∠BAC和∠BAD,
∠ABC和∠ABD,
∠C和∠D.
(2)
应用交流
A
B
C
D
E
△ABC≌△ADE
对应边:AB和AD,
AC和AE,
BC和DE;
对应角:∠ACB和∠AED,
∠B和∠D,
∠BAC和∠DAE.
规律二:有公共角的,公共角是对应角.
(3)
应用交流
A
C
B
D
规律三:有对顶角的,对顶角是对应角.
△AOC≌△BOD
对应边:OA和OB,OC和OD,
AC和BD;
对应角:∠AOC和∠BOD,
∠A和∠B,
∠C和∠D.
O
(4)
应用交流
A
B
C
F
D
E
△ABC≌△DEF
对应边:AB和DE,
AC和DF,
BC和EF;
对应角:∠A和∠D,
∠B和∠E,
∠C和∠F.
规律四:
最长的边是对应边,
最短的边是对应边;
规律五:
最大的角是对应角,
最小的角是对应角.
(5)
应用交流
3.有公共角的,公共角一定是对应角。
4.对应角所对的边是对应边,
对应边所对的角是对应角.
5.在两个全等三角形中
最长边对最长边,最短边对最短边;
最大角对最大角,最小角对最小角。
1.有公共边的,公共边一定是对应边。
2.有对顶角的,对顶角一定是对应角。
规律总结
6.根据书写规范,按对应顶点找对应边(角)。
1、有公共边
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共顶点
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
典型图例
写出下列全等三角形中相等的边和角:
A
B
C
D
课堂练习
△ABD≌△CBD
(1)
AB=CB,
AD=CD,
BD=BD;
∠A=∠C,
∠ABD=∠CBD,
∠ADB=∠CDB.
A
B
C
D
O
(2)
△OAB≌△OCD
OA=OC,
OB=OD,
AB=CD;
∠A=∠C,∠B=∠D,
∠AOB=∠COD.
△ABC≌△ADE
(3)
AB=AD,
AC=AE,
BC=DE;
∠B=∠D,
∠C=∠E,
∠BAC=∠DAE.
(4)
△ADE≌△CBF
A
B
D
C
E
B
F
C
D
A
E
AD=CB,
AE=CF,
DE=BF;
∠A=∠C,
∠ADE=∠CBF,
∠AED=∠CFB.
△ABN≌△ACM
(5)
AB=AC,
AN=AM,
BN=CM;
∠B=∠C,
∠ANB=∠AMC,
∠BAN=∠CAM.
(6)
△AOB≌△DOC
AB=DC,
AO=DO,
BO=CO;
∠A=∠D,
∠AOB=∠DOC,
∠ABO=∠DCO.
A
B
M
N
C
A
B
C
D
O
△ABC≌△DCB
AB=DC,
AC=DB,
BC=CB;
∠A=∠D,
∠ABC=∠DCB,
∠ACB=∠DBC.
1、若△AOC≌△BOD,
则AC=
,∠A=
.
A
B
O
C
D
2、若△ABD≌△ACE,
则BD=
,∠BDA=
.
3、若△ABC≌△CDA,
则AB=
,∠BAC=
.
A
B
C
D
填空:
BD
∠B
CE
∠CEA
CD
∠DCA
A
B
C
D
E
公共点
公共角
公共边
A
D
C
B
A
E
B
D
C
A
B
C
D
E
F
(2)已知△ABC≌△CDA,
则AC边的对应边为
.
(1)已知△ABC≌△ADE,
则∠A的对应角为
.
(3)已知△ABC≌△DEF,
则AB边的对应边为
,
∠C的对应角为
.
CA
∠A
DE
∠F
填一填:
1、如图,已知△AOC≌△BOD,
求证:AC∥BD.
拓展
提高
证明:
∵△AOC≌△BOD,
(已知)
∴∠A=∠B,
(全等三角形的对应角相等)
∴AC∥BD.
(内错角相等,两直线平行)
A
B
D
C
O
2、如图,已知△ABD≌△ACE,且∠C=50?,
∠A=30?,AC=
8,AE
=
5,求∠ADB及DC.
A
E
B
C
D
解:
∵△ABD≌△ACE,
∴∠B=∠C=50°
?
(全等三角形的对应角相等)
∵∠A=30°,
∴∠ADB=180°-∠A-∠B
=100°.
∵△ABD≌△ACE,
∴AD=AE=5.
(全等三角形的对应边相等)
∵AC=
8,
∴DC=AC-AD=3.
5
5
3
3、如图,
△EFG≌△NMH.
(2)如果EF=2.1cm,EH=1.1cm,HN=3.3cm,
求NM、HG的长.
(1)请找出对应边和对应角。
N
M
F
G
E
H
(3)在(2)的条件下,若FG=4cm,
求△NMH的周长.
2.1
1.1
3.3
2.1
2.2
(4)这两个三角形的面积相等吗?
互相重合的角叫做
.
互相重合的边叫做
,
其中:互相重合的顶点叫做
,
2.
叫全等三角形.
1.能够重合的两个图形叫做
。
全等形
4.全等三角形的
和
相等.
对应边
对应角
对应顶点
课堂小结
能够完全重合的两个三角形
3.“全等”用符号“
”来表示,
读作“
”.
对应边
对应角
5.书写全等式时要求把对应字母放在对应
的位置上.
全等于
≌
