人教版八年级数学上册 12.2.2用“SAS”证三角形全等 同步训练卷(word版,含答案)
文档属性
| 名称 | 人教版八年级数学上册 12.2.2用“SAS”证三角形全等 同步训练卷(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 283.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 07:10:22 | ||
图片预览



文档简介
人教版八年级数学上册
12.2.2
用“SAS”证三角形全等
同步训练卷
一、选择题(共10小题,3
10=30)
1.使△ABC≌△A′B′C′的条件是(
)
A.AB=A′B′,∠B=∠B′,AC=A′C′
B.AB=A′B′,∠A=∠A′,BC=B′C′
C.AB=A′C′,∠B=∠B′,BC=B′C′
D.AC=A′C′,∠C=∠C′,BC=B′C
2.如图,a,b,c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是( )
3.如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充下列哪一个条件后,能应用“SAS”判定△ABC≌△DEF?( )
A.BF=EC
B.∠ACB=∠DFE
C.AC=DF
D.∠A=∠D
4.如图,AC与BD相交于点O.若OA=OD,则要用“SAS”证明△AOB≌△DOC,还需添加的条件是( )
A.AB=DC
B.OB=OC
C.∠A=∠D
D.∠AOB=∠DOC
5.如图,AB=DB,BC=BE,欲使△ABC≌△DBE,需要增加的条件是(
)
A.∠A=∠D
B.∠E=∠C
C.∠A=∠E
D.∠1=∠2
6.
如图,将两根铜条AA′,BB′的中点O连在一起,使AA′,BB′可以绕着点O自由转动,就做成了一个测量工件,则AB的长等于内槽宽A′B′,那么判定△AOB≌△A′OB′的理由是( )
A.边角边
B.角边角
C.边边边
D.角角边
7.如图,已知∠1=∠2,AB=AD,AE=AC,若∠B=30°,则∠D的度数为( )
A.20°
B.30°
C.40°
D.无法确定
8.如图,AC,BD相交于点E,AC=BD,AE=BE,∠B=35°,∠1=95°,则∠D的度数是( )
A.60°
B.35°
C.50°
D.75°
9.如图,AB=AC,AD=AE,若要得到“△ABD≌△ACE”,必须添加一个条件,则下列所添条件不成立的是(
)
A.BD=CE
B.∠ABD=∠ACE
C.∠BAD=∠CAE
D.∠BAC=∠DAE
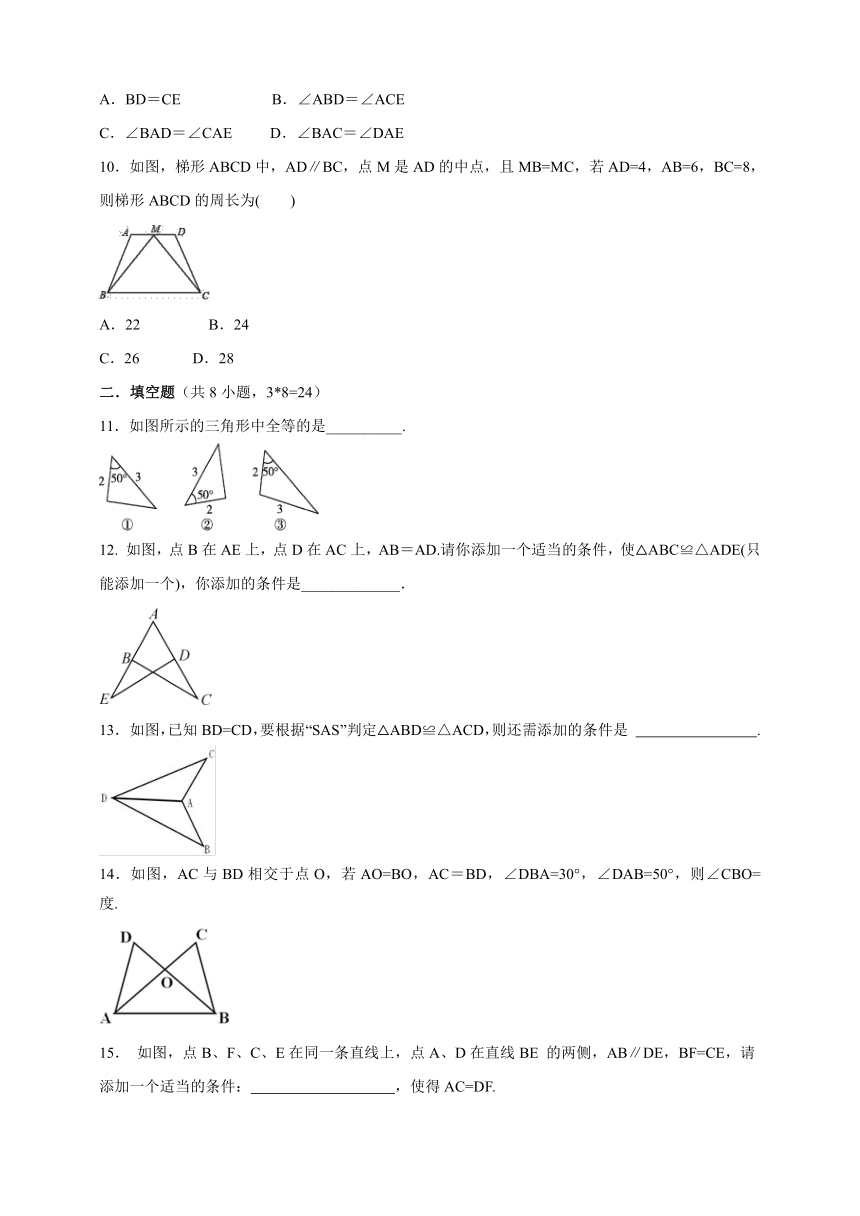
10.如图,梯形ABCD中,AD∥BC,点M是AD的中点,且MB=MC,若AD=4,AB=6,BC=8,则梯形ABCD的周长为(
)
A.22
B.24
C.26
D.28
二.填空题(共8小题,3
8=24)
11.如图所示的三角形中全等的是__________.
12.
如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个),你添加的条件是_____________.
13.
如图,已知BD=CD,要根据“SAS”判定△ABD≌△ACD,则还需添加的条件是
.
14.如图,AC与BD相交于点O,若AO=BO,AC=BD,∠DBA=30°,∠DAB=50°,则∠CBO=
度.
15.
如图,点B、F、C、E在同一条直线上,点A、D在直线BE
的两侧,AB∥DE,BF=CE,请添加一个适当的条件:
,使得AC=DF.
16.如图,OA=OB,OC=OD,∠O=60°,∠C=25°,则∠BED=
度.
17.如图,已知△ABC,BA=BC,BD平分∠ABC,若∠C=40°,则∠ABE为
度.
18.△ABC中,AB=6,AC=2,AD是BC边上的中线,则AD的取值范围是
.
三.解答题(共7小题,
46分)
19.(6分)
如图,已知线段AC,BD相交于点E,AE=DE,BE=CE.求证:△ABE≌△DCE.
20.(6分)
如图,已知AC平分∠BAD,AB=AD.求证:△ABC≌△ADC.
21.(6分)
如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
22.(6分)
如图,C是线段AB的中点,CD=BE,CD∥BE.求证:∠D=∠E.
23.(6分)
如图,AB=AD,AC=AE,∠1=∠2,求证:
(1)△ABC≌△ADE;
(2)CB=ED.
24.(8分)
如图,点A,F,C,D在同一条直线上,AB∥DE,AB=DE,AF=DC.求证:BC∥EF.
25.(8分)
如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
(1)求证:△ABE≌△DBE.
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
参考答案
1-5
DBABD
6-10ABABB
11.
①与②
12.
AE=AC
13.
∠CDA=∠BDA
14.
20
15.
AB=DE
16.
70
17.
80
18.
2
<
AD
<
4
19.
证明:在△ABE和△DCE中,
∴△ABE≌△DCE.
20.
证明:∵AC平分∠BAD,∴∠BAC=∠DAC.
在△ABC和△ADC中,
∴△ABC≌△ADC.
21.
证明:∵BE=CF,∴BF=CE.
在△ABF和△DCE中,
∴△ABF≌△DCE,∴∠A=∠D.
22.
解:∵C是线段AB的中点,∴AC=CB,
∵CD∥BE,∴∠ACD=∠B,
在△ACD和△CBE中,
∴△ACD≌△CBE(SAS),∴∠D=∠E
23.
解:(1)∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,
即∠BAC=∠DAE,又∵AB=AD,AC=AE,
∴△ABC≌△ADE(SAS)
(2)∵△ABC≌△ADE,∴CB=ED
24.
证明:∵AB∥DE,∴∠A=∠D.
∵AF=DC,∴AC=DF.
在△ABC和△EDF中,
∴△ABC≌△EDF,
∴∠BCA=∠EFD.∴BC∥EF.
25.
证明:(1)∵BE平分∠ABC,∴∠ABE=∠DBE,
在△ABE和△DBE中,
∴△ABE≌△DBE(SAS).
(2)∵∠A=100°,∠C=50°,∴∠ABC=30°.
∵BE平分∠ABC,
∴∠ABE=∠DBE=∠ABC=15°.
在△ABE中,∠AEB=180°-∠A-∠ABE=
180°-100°-15°=65°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
12.2.2
用“SAS”证三角形全等
同步训练卷
一、选择题(共10小题,3
10=30)
1.使△ABC≌△A′B′C′的条件是(
)
A.AB=A′B′,∠B=∠B′,AC=A′C′
B.AB=A′B′,∠A=∠A′,BC=B′C′
C.AB=A′C′,∠B=∠B′,BC=B′C′
D.AC=A′C′,∠C=∠C′,BC=B′C
2.如图,a,b,c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是( )
3.如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充下列哪一个条件后,能应用“SAS”判定△ABC≌△DEF?( )
A.BF=EC
B.∠ACB=∠DFE
C.AC=DF
D.∠A=∠D
4.如图,AC与BD相交于点O.若OA=OD,则要用“SAS”证明△AOB≌△DOC,还需添加的条件是( )
A.AB=DC
B.OB=OC
C.∠A=∠D
D.∠AOB=∠DOC
5.如图,AB=DB,BC=BE,欲使△ABC≌△DBE,需要增加的条件是(
)
A.∠A=∠D
B.∠E=∠C
C.∠A=∠E
D.∠1=∠2
6.
如图,将两根铜条AA′,BB′的中点O连在一起,使AA′,BB′可以绕着点O自由转动,就做成了一个测量工件,则AB的长等于内槽宽A′B′,那么判定△AOB≌△A′OB′的理由是( )
A.边角边
B.角边角
C.边边边
D.角角边
7.如图,已知∠1=∠2,AB=AD,AE=AC,若∠B=30°,则∠D的度数为( )
A.20°
B.30°
C.40°
D.无法确定
8.如图,AC,BD相交于点E,AC=BD,AE=BE,∠B=35°,∠1=95°,则∠D的度数是( )
A.60°
B.35°
C.50°
D.75°
9.如图,AB=AC,AD=AE,若要得到“△ABD≌△ACE”,必须添加一个条件,则下列所添条件不成立的是(
)
A.BD=CE
B.∠ABD=∠ACE
C.∠BAD=∠CAE
D.∠BAC=∠DAE
10.如图,梯形ABCD中,AD∥BC,点M是AD的中点,且MB=MC,若AD=4,AB=6,BC=8,则梯形ABCD的周长为(
)
A.22
B.24
C.26
D.28
二.填空题(共8小题,3
8=24)
11.如图所示的三角形中全等的是__________.
12.
如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个),你添加的条件是_____________.
13.
如图,已知BD=CD,要根据“SAS”判定△ABD≌△ACD,则还需添加的条件是
.
14.如图,AC与BD相交于点O,若AO=BO,AC=BD,∠DBA=30°,∠DAB=50°,则∠CBO=
度.
15.
如图,点B、F、C、E在同一条直线上,点A、D在直线BE
的两侧,AB∥DE,BF=CE,请添加一个适当的条件:
,使得AC=DF.
16.如图,OA=OB,OC=OD,∠O=60°,∠C=25°,则∠BED=
度.
17.如图,已知△ABC,BA=BC,BD平分∠ABC,若∠C=40°,则∠ABE为
度.
18.△ABC中,AB=6,AC=2,AD是BC边上的中线,则AD的取值范围是
.
三.解答题(共7小题,
46分)
19.(6分)
如图,已知线段AC,BD相交于点E,AE=DE,BE=CE.求证:△ABE≌△DCE.
20.(6分)
如图,已知AC平分∠BAD,AB=AD.求证:△ABC≌△ADC.
21.(6分)
如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
22.(6分)
如图,C是线段AB的中点,CD=BE,CD∥BE.求证:∠D=∠E.
23.(6分)
如图,AB=AD,AC=AE,∠1=∠2,求证:
(1)△ABC≌△ADE;
(2)CB=ED.
24.(8分)
如图,点A,F,C,D在同一条直线上,AB∥DE,AB=DE,AF=DC.求证:BC∥EF.
25.(8分)
如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
(1)求证:△ABE≌△DBE.
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
参考答案
1-5
DBABD
6-10ABABB
11.
①与②
12.
AE=AC
13.
∠CDA=∠BDA
14.
20
15.
AB=DE
16.
70
17.
80
18.
2
<
AD
<
4
19.
证明:在△ABE和△DCE中,
∴△ABE≌△DCE.
20.
证明:∵AC平分∠BAD,∴∠BAC=∠DAC.
在△ABC和△ADC中,
∴△ABC≌△ADC.
21.
证明:∵BE=CF,∴BF=CE.
在△ABF和△DCE中,
∴△ABF≌△DCE,∴∠A=∠D.
22.
解:∵C是线段AB的中点,∴AC=CB,
∵CD∥BE,∴∠ACD=∠B,
在△ACD和△CBE中,
∴△ACD≌△CBE(SAS),∴∠D=∠E
23.
解:(1)∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,
即∠BAC=∠DAE,又∵AB=AD,AC=AE,
∴△ABC≌△ADE(SAS)
(2)∵△ABC≌△ADE,∴CB=ED
24.
证明:∵AB∥DE,∴∠A=∠D.
∵AF=DC,∴AC=DF.
在△ABC和△EDF中,
∴△ABC≌△EDF,
∴∠BCA=∠EFD.∴BC∥EF.
25.
证明:(1)∵BE平分∠ABC,∴∠ABE=∠DBE,
在△ABE和△DBE中,
∴△ABE≌△DBE(SAS).
(2)∵∠A=100°,∠C=50°,∴∠ABC=30°.
∵BE平分∠ABC,
∴∠ABE=∠DBE=∠ABC=15°.
在△ABE中,∠AEB=180°-∠A-∠ABE=
180°-100°-15°=65°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
