人教版八年级数学上册12.2 三角形全等的判定(三)(ASA,AAS)同步练习(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册12.2 三角形全等的判定(三)(ASA,AAS)同步练习(Word版 含答案) | 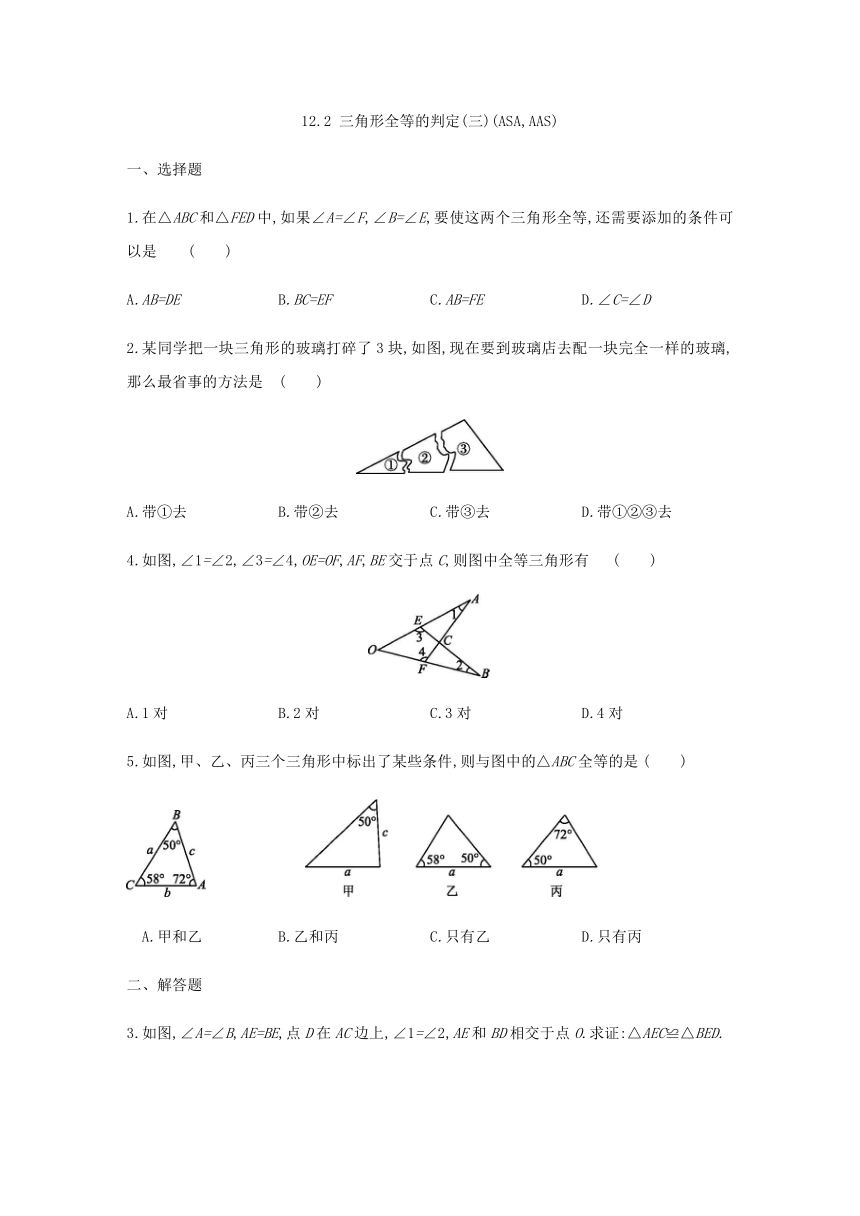 | |
| 格式 | zip | ||
| 文件大小 | 119.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 07:06:05 | ||
图片预览




文档简介
12.2
三角形全等的判定(三)(ASA,AAS)
一、选择题
1.在△ABC和△FED中,如果∠A=∠F,∠B=∠E,要使这两个三角形全等,还需要添加的条件可以是
( )
A.AB=DE
B.BC=EF
C.AB=FE
D.∠C=∠D
2.某同学把一块三角形的玻璃打碎了3块,如图,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是
( )
A.带①去
B.带②去
C.带③去
D.带①②③去
4.如图,∠1=∠2,∠3=∠4,OE=OF,AF,BE交于点C,则图中全等三角形有
( )
A.1对
B.2对
C.3对
D.4对
5.如图,甲、乙、丙三个三角形中标出了某些条件,则与图中的△ABC全等的是
( )
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
二、解答题
3.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED.
6.如图,已知AB=AD,∠C=∠E,∠1=∠2.
求证:△ABC≌△ADE.
7.如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
求证:D是BC的中点.
9.阅读下题及其证明过程:
已知:如图,D是△ABC中BC边上一点,E是AD上一点,EB=EC,∠ABE=∠ACE.求证:
∠BAE=∠CAE.(提示:三角形中相等的边所对的角相等,相等的角所对的边也相等)
证明:在△AEB和△AEC中,
∴△AEB≌△AEC.……第一步
∴∠BAE=∠CAE.……第二步
上面的证明过程是否正确?若正确,请写出每一步推理的依据;若不正确,请指出错在哪一步,并写出你认为正确的证明过程.
10.如图,小强在河的一边,要测河面的一只船B与对岸码头A之间的距离,他的做法如下:
①在岸边确定一点C,使点C与A,B在同一直线上;
②在与AC垂直的方向画线段CD,取CD的中点O;
③画DF⊥CD,并使点F,O,A在同一直线上;
④在线段DF上找一点E,使点E与O,B共线.
他说测出线段EF的长就是船B与对岸码头A之间的距离.他这样做有道理吗?为什么?
11.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,P,Q是边AC,BC上的两个动点,PD⊥AB于点D,QE⊥AB于点E,设点P,Q运动的时间是t秒(t>0).
(1)如图①,若点P,Q分别从A,B两点同时出发,沿AC,BC向点C匀速运动,运动速度都为每秒1个单位长度,其中一点到达终点C后,另一点也随之停止运动,在运动过程中△APD和△QBE是否保持全等?判断并说明理由.
(2)若点P从点C出发沿CA以每秒3个单位长度的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回到点C停止运动;点Q仍从点B出发沿BC以每秒1个单位长度的速度向点C匀速运动,到达点C后停止运动,当t为何值时,△APD和△QBE全等?
答案
1.C 2.C
3.证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
又∵在△AOD和△BOE中,∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,∴∠AEC=∠BED.
在△AEC和△BED中,
∴△AEC≌△BED.
4.B [解析]
在△OAF和△OBE中,
所以△OAF≌△OBE.所以OA=OB.所以AE=BF.
在△ECA和△FCB中,
所以△ECA≌△FCB.
5.B
6.证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,
∴△ABC≌△ADE(AAS).
7.证明:∵AF∥BC,∴∠AFE=∠DCE.
∵E为AD的中点,∴AE=DE.
在△AEF和△DEC中,
∴△AEF≌△DEC(AAS).∴AF=DC.
又∵AF=BD,∴DC=BD,即D是BC的中点.
8.两边和其中一边的对角分别相等的两个三角形不一定全等
9.解:不正确,错在第一步.正确的证明过程如下:
∵在△BEC中,EB=EC,∴∠EBC=∠ECB.
又∵∠ABE=∠ACE,
∴∠ABC=∠ACB.∴AB=AC.
在△AEB和△AEC中,
∴△AEB≌△AEC.∴∠BAE=∠CAE.
10.解:有道理.
理由:∵AC⊥CD,DF⊥CD,∴∠C=∠D=90°.
∵O为CD的中点,∴CO=DO.
在△ACO和△FDO中,
∴△ACO≌△FDO(ASA).
∴AO=FO,∠A=∠F.
在△ABO和△FEO中,
∴△ABO≌△FEO(ASA).∴AB=EF.
故测出EF的长就是船B与对岸码头A之间的距离.
11.解:(1)△APD和△QBE保持全等.
理由:∵PD⊥AB,QE⊥AB,
∴∠ADP=∠QEB=90°.
又∵∠C=90°,
∴∠A+∠APD=∠A+∠B=90°.
∴∠APD=∠B.
由题意可知AP=QB=t.
在△ADP与△QEB中,
∴△ADP≌△QEB.
(2)①当0②当≤t≤时,点P从点A向点C运动,则AP=3t-8,QB=t.若△ADP≌△QEB,则AP=QB,即3t-8=t,解得t=4.
综上所述,当t的值为2或4时,△APD和△QBE全等.
三角形全等的判定(三)(ASA,AAS)
一、选择题
1.在△ABC和△FED中,如果∠A=∠F,∠B=∠E,要使这两个三角形全等,还需要添加的条件可以是
( )
A.AB=DE
B.BC=EF
C.AB=FE
D.∠C=∠D
2.某同学把一块三角形的玻璃打碎了3块,如图,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是
( )
A.带①去
B.带②去
C.带③去
D.带①②③去
4.如图,∠1=∠2,∠3=∠4,OE=OF,AF,BE交于点C,则图中全等三角形有
( )
A.1对
B.2对
C.3对
D.4对
5.如图,甲、乙、丙三个三角形中标出了某些条件,则与图中的△ABC全等的是
( )
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
二、解答题
3.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED.
6.如图,已知AB=AD,∠C=∠E,∠1=∠2.
求证:△ABC≌△ADE.
7.如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
求证:D是BC的中点.
9.阅读下题及其证明过程:
已知:如图,D是△ABC中BC边上一点,E是AD上一点,EB=EC,∠ABE=∠ACE.求证:
∠BAE=∠CAE.(提示:三角形中相等的边所对的角相等,相等的角所对的边也相等)
证明:在△AEB和△AEC中,
∴△AEB≌△AEC.……第一步
∴∠BAE=∠CAE.……第二步
上面的证明过程是否正确?若正确,请写出每一步推理的依据;若不正确,请指出错在哪一步,并写出你认为正确的证明过程.
10.如图,小强在河的一边,要测河面的一只船B与对岸码头A之间的距离,他的做法如下:
①在岸边确定一点C,使点C与A,B在同一直线上;
②在与AC垂直的方向画线段CD,取CD的中点O;
③画DF⊥CD,并使点F,O,A在同一直线上;
④在线段DF上找一点E,使点E与O,B共线.
他说测出线段EF的长就是船B与对岸码头A之间的距离.他这样做有道理吗?为什么?
11.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,P,Q是边AC,BC上的两个动点,PD⊥AB于点D,QE⊥AB于点E,设点P,Q运动的时间是t秒(t>0).
(1)如图①,若点P,Q分别从A,B两点同时出发,沿AC,BC向点C匀速运动,运动速度都为每秒1个单位长度,其中一点到达终点C后,另一点也随之停止运动,在运动过程中△APD和△QBE是否保持全等?判断并说明理由.
(2)若点P从点C出发沿CA以每秒3个单位长度的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回到点C停止运动;点Q仍从点B出发沿BC以每秒1个单位长度的速度向点C匀速运动,到达点C后停止运动,当t为何值时,△APD和△QBE全等?
答案
1.C 2.C
3.证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
又∵在△AOD和△BOE中,∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,∴∠AEC=∠BED.
在△AEC和△BED中,
∴△AEC≌△BED.
4.B [解析]
在△OAF和△OBE中,
所以△OAF≌△OBE.所以OA=OB.所以AE=BF.
在△ECA和△FCB中,
所以△ECA≌△FCB.
5.B
6.证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,
∴△ABC≌△ADE(AAS).
7.证明:∵AF∥BC,∴∠AFE=∠DCE.
∵E为AD的中点,∴AE=DE.
在△AEF和△DEC中,
∴△AEF≌△DEC(AAS).∴AF=DC.
又∵AF=BD,∴DC=BD,即D是BC的中点.
8.两边和其中一边的对角分别相等的两个三角形不一定全等
9.解:不正确,错在第一步.正确的证明过程如下:
∵在△BEC中,EB=EC,∴∠EBC=∠ECB.
又∵∠ABE=∠ACE,
∴∠ABC=∠ACB.∴AB=AC.
在△AEB和△AEC中,
∴△AEB≌△AEC.∴∠BAE=∠CAE.
10.解:有道理.
理由:∵AC⊥CD,DF⊥CD,∴∠C=∠D=90°.
∵O为CD的中点,∴CO=DO.
在△ACO和△FDO中,
∴△ACO≌△FDO(ASA).
∴AO=FO,∠A=∠F.
在△ABO和△FEO中,
∴△ABO≌△FEO(ASA).∴AB=EF.
故测出EF的长就是船B与对岸码头A之间的距离.
11.解:(1)△APD和△QBE保持全等.
理由:∵PD⊥AB,QE⊥AB,
∴∠ADP=∠QEB=90°.
又∵∠C=90°,
∴∠A+∠APD=∠A+∠B=90°.
∴∠APD=∠B.
由题意可知AP=QB=t.
在△ADP与△QEB中,
∴△ADP≌△QEB.
(2)①当0
综上所述,当t的值为2或4时,△APD和△QBE全等.
