人教版八年级数学上册课件:13.1.2线段的垂直平分线的性质(共16张PPT)
文档属性
| 名称 | 人教版八年级数学上册课件:13.1.2线段的垂直平分线的性质(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 08:30:47 | ||
图片预览




文档简介
(共16张PPT)
13.1.2
线段的垂直平分线的性质
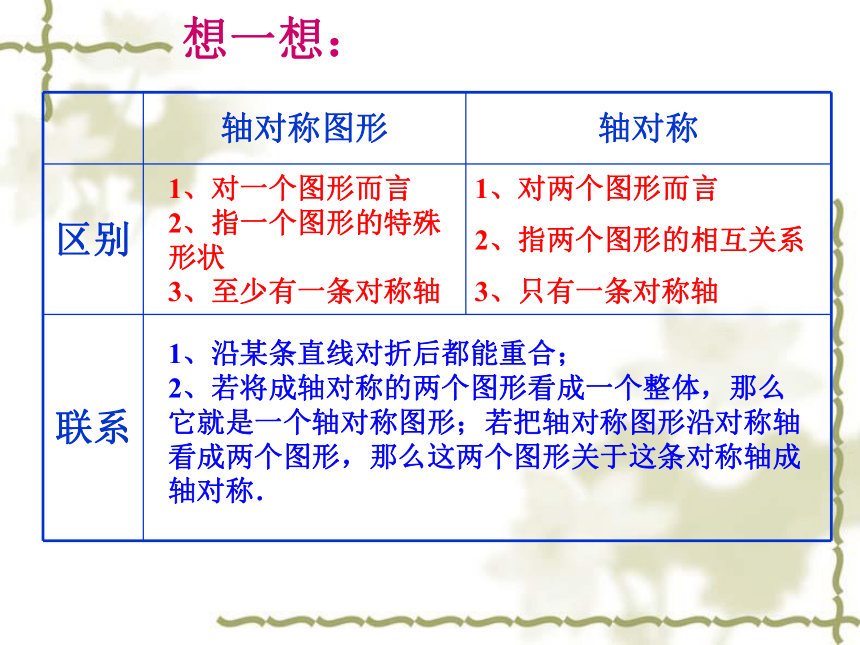
想一想:
轴对称图形
轴对称
区别
联系
1、对两个图形而言
2、指两个图形的相互关系
3、只有一条对称轴
1、对一个图形而言
2、指一个图形的特殊形状
3、至少有一条对称轴
1、沿某条直线对折后都能重合;
2、若将成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形;若把轴对称图形沿对称轴看成两个图形,那么这两个图形关于这条对称轴成轴对称.
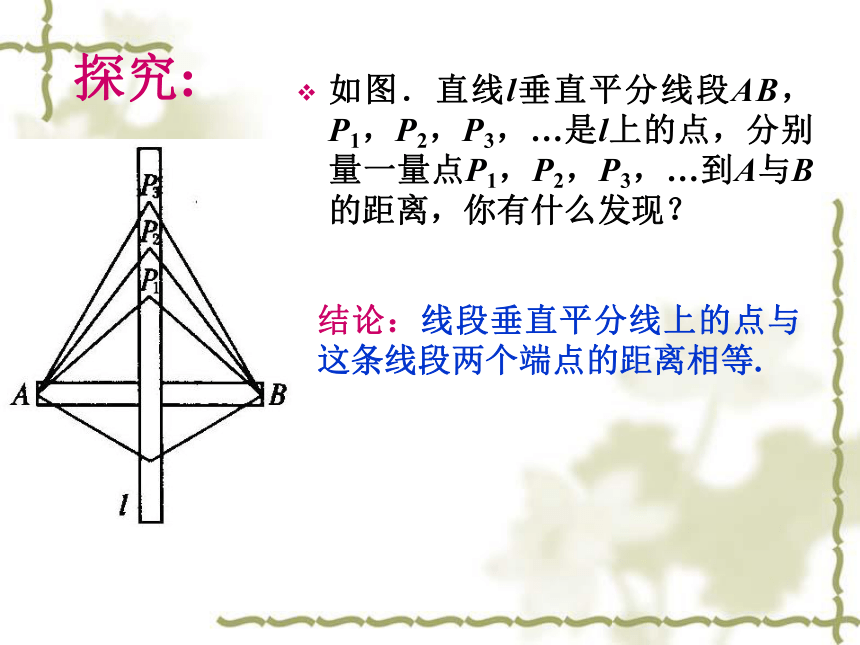
探究:
如图.直线l垂直平分线段AB,P1,P2,P3,…是l上的点,分别量一量点P1,P2,P3,…到A与B的距离,你有什么发现?
结论:线段垂直平分线上的点与这条线段两个端点的距离相等.
线段垂直平分线上的点与这条线段两个端点距离相等.
你能证明这一结论吗?
已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.
求证:PA=PB.
A
C
B
P
M
N
证明:∵MN⊥AB
∴∠PCA=∠PCB
∵AC=BC,PC=PC
∴
△APC≌△BPC(SAS)
∴PA=PB
探究:
定理
:线段垂直平分线上的点到这条线段两个端点距离相等.
提示:这个结论是经常用来证明两条线段相等的根据之一.
几何语言:
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点与这条线段两个端点距离相等).
A
C
B
P
M
N
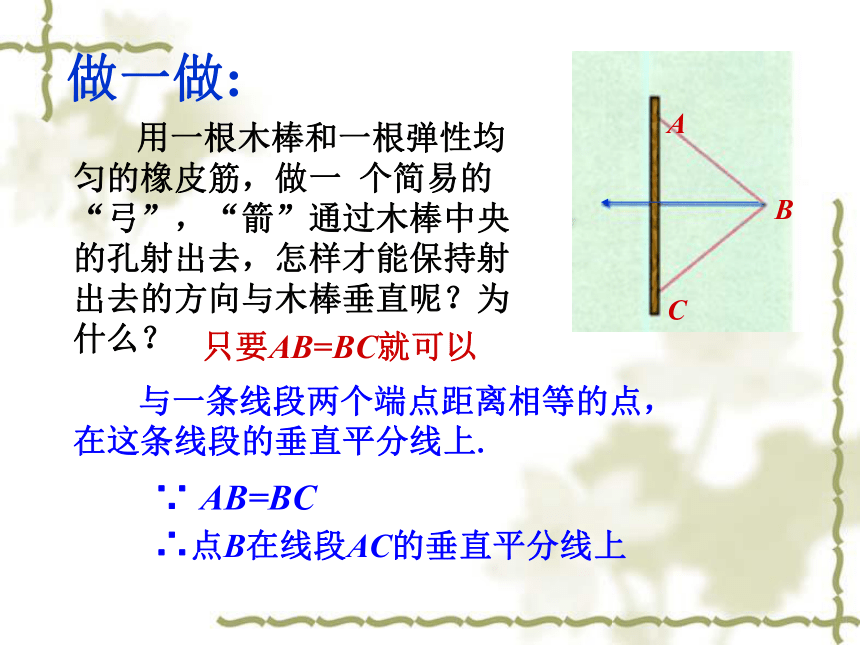
探究:
用一根木棒和一根弹性均匀的橡皮筋,做一
个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的方向与木棒垂直呢?为什么?
C
B
A
只要AB=BC就可以
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
∴点B在线段AC的垂直平分线上
∵
AB=BC
做一做:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
你能证明这个结论吗?
结论:
P
A
B
C
已知:PA=PB,求证:点P在线段AB的垂直平分线上.
证明:过点P作PC
⊥AB于C
∴∠PCA=∠PCB=90°
∵PA=PB,PC=PC
∴
△APC≌△BPC(HL)
∴AC=BC
定理:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
几何语言:
∵PA=PB(已知)
∴点P在AB的垂直平分线上(与一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.
A
C
B
P
M
N
探究:
结论:
线段垂直平分线上的点与这条线段两个端点的距离相等.
反之,与线段两个端点的距离相等的点在这条线段垂直平分线上.
所以,线段垂直平分线可以看作到线段两端的距离相等的所有点的集合.
拓展:
如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长.
N
M
C
B
A
1、
如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC
、CE
的长度有什么关系?AB+BD
与DE有什么关系?
AB=AC=CE
AB+BD=DE
练习:
A
C
D
B
D
2、如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
∵AB=AC
MB=MC
∴直线AM垂直平分线段BC
(与一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
练习:
A
C
M
B
P
A
B
C
结论:三角形三边的垂直平分线交于一点,并且这点到三个顶点的距离相等.
练习:
3、已知:
△ABC中,边AB、
BC的垂直平分线交于点P.
求证:PA=PB=PC.
4、如图,七(1)班与七(2)班两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且PM=PN,请你用折纸的方法找出P点并说明理由.
M
N
B
C
A
练习:
(3)与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
(1)垂直并且平分线段的直线叫做这条线段的垂直平分线.简称中垂线.
(2)线段垂直平分线上的点与这条线段
的两个端点距离相等.
通过今天这节课你有什么收获?
感悟与反思:
12.3
角的平分线
O
D
E
A
B
P
C
定理1
在角的平分线上的点到这个角的两边的距离相等.
定理2
到一个角的两边的距离相等的点,在这个角的平分线上.
角的平分线是到角的两边距离相等的所有点的集合.
定
理
线段垂直平分线上的点和这条线段两个端点的距离相等.
逆定理
和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合.
13.1
线段的垂直平分线
A
B
M
N
P
点的集合是一条射线
点的集合是一条直线
13.1.2
线段的垂直平分线的性质
想一想:
轴对称图形
轴对称
区别
联系
1、对两个图形而言
2、指两个图形的相互关系
3、只有一条对称轴
1、对一个图形而言
2、指一个图形的特殊形状
3、至少有一条对称轴
1、沿某条直线对折后都能重合;
2、若将成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形;若把轴对称图形沿对称轴看成两个图形,那么这两个图形关于这条对称轴成轴对称.
探究:
如图.直线l垂直平分线段AB,P1,P2,P3,…是l上的点,分别量一量点P1,P2,P3,…到A与B的距离,你有什么发现?
结论:线段垂直平分线上的点与这条线段两个端点的距离相等.
线段垂直平分线上的点与这条线段两个端点距离相等.
你能证明这一结论吗?
已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.
求证:PA=PB.
A
C
B
P
M
N
证明:∵MN⊥AB
∴∠PCA=∠PCB
∵AC=BC,PC=PC
∴
△APC≌△BPC(SAS)
∴PA=PB
探究:
定理
:线段垂直平分线上的点到这条线段两个端点距离相等.
提示:这个结论是经常用来证明两条线段相等的根据之一.
几何语言:
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点与这条线段两个端点距离相等).
A
C
B
P
M
N
探究:
用一根木棒和一根弹性均匀的橡皮筋,做一
个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的方向与木棒垂直呢?为什么?
C
B
A
只要AB=BC就可以
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
∴点B在线段AC的垂直平分线上
∵
AB=BC
做一做:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
你能证明这个结论吗?
结论:
P
A
B
C
已知:PA=PB,求证:点P在线段AB的垂直平分线上.
证明:过点P作PC
⊥AB于C
∴∠PCA=∠PCB=90°
∵PA=PB,PC=PC
∴
△APC≌△BPC(HL)
∴AC=BC
定理:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
几何语言:
∵PA=PB(已知)
∴点P在AB的垂直平分线上(与一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.
A
C
B
P
M
N
探究:
结论:
线段垂直平分线上的点与这条线段两个端点的距离相等.
反之,与线段两个端点的距离相等的点在这条线段垂直平分线上.
所以,线段垂直平分线可以看作到线段两端的距离相等的所有点的集合.
拓展:
如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长.
N
M
C
B
A
1、
如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC
、CE
的长度有什么关系?AB+BD
与DE有什么关系?
AB=AC=CE
AB+BD=DE
练习:
A
C
D
B
D
2、如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
∵AB=AC
MB=MC
∴直线AM垂直平分线段BC
(与一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
练习:
A
C
M
B
P
A
B
C
结论:三角形三边的垂直平分线交于一点,并且这点到三个顶点的距离相等.
练习:
3、已知:
△ABC中,边AB、
BC的垂直平分线交于点P.
求证:PA=PB=PC.
4、如图,七(1)班与七(2)班两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且PM=PN,请你用折纸的方法找出P点并说明理由.
M
N
B
C
A
练习:
(3)与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
(1)垂直并且平分线段的直线叫做这条线段的垂直平分线.简称中垂线.
(2)线段垂直平分线上的点与这条线段
的两个端点距离相等.
通过今天这节课你有什么收获?
感悟与反思:
12.3
角的平分线
O
D
E
A
B
P
C
定理1
在角的平分线上的点到这个角的两边的距离相等.
定理2
到一个角的两边的距离相等的点,在这个角的平分线上.
角的平分线是到角的两边距离相等的所有点的集合.
定
理
线段垂直平分线上的点和这条线段两个端点的距离相等.
逆定理
和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合.
13.1
线段的垂直平分线
A
B
M
N
P
点的集合是一条射线
点的集合是一条直线
