人教版八年级数学上册同步练习:12.2 三角形全等的判定(SAS)(word版,含答案)
文档属性
| 名称 | 人教版八年级数学上册同步练习:12.2 三角形全等的判定(SAS)(word版,含答案) | 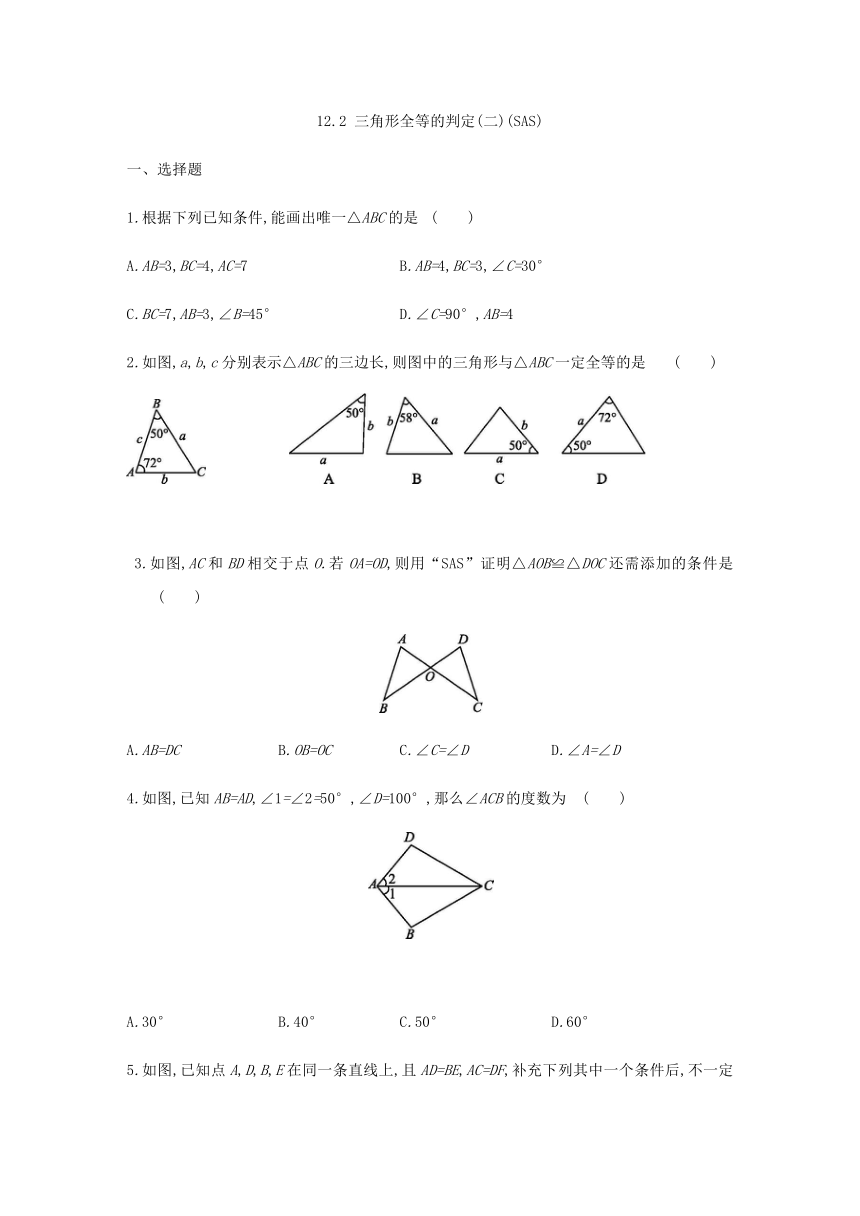 | |
| 格式 | zip | ||
| 文件大小 | 162.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 07:00:54 | ||
图片预览

文档简介
12.2
三角形全等的判定(二)(SAS)
一、选择题
1.根据下列已知条件,能画出唯一△ABC的是
( )
A.AB=3,BC=4,AC=7
B.AB=4,BC=3,∠C=30°
C.BC=7,AB=3,∠B=45°
D.∠C=90°,AB=4
2.如图,a,b,c分别表示△ABC的三边长,则图中的三角形与△ABC一定全等的是
( )
3.如图,AC和BD相交于点O.若OA=OD,则用“SAS”证明△AOB≌△DOC还需添加的条件是
( )
A.AB=DC
B.OB=OC
C.∠C=∠D
D.∠A=∠D
4.如图,已知AB=AD,∠1=∠2=50°,∠D=100°,那么∠ACB的度数为
( )
A.30°
B.40°
C.50°
D.60°
5.如图,已知点A,D,B,E在同一条直线上,且AD=BE,AC=DF,补充下列其中一个条件后,不一定能得到△ABC≌△DEF的是
( )
A.BC=EF
B.AC∥DF
C.∠C=∠F
D.∠BAC=∠EDF
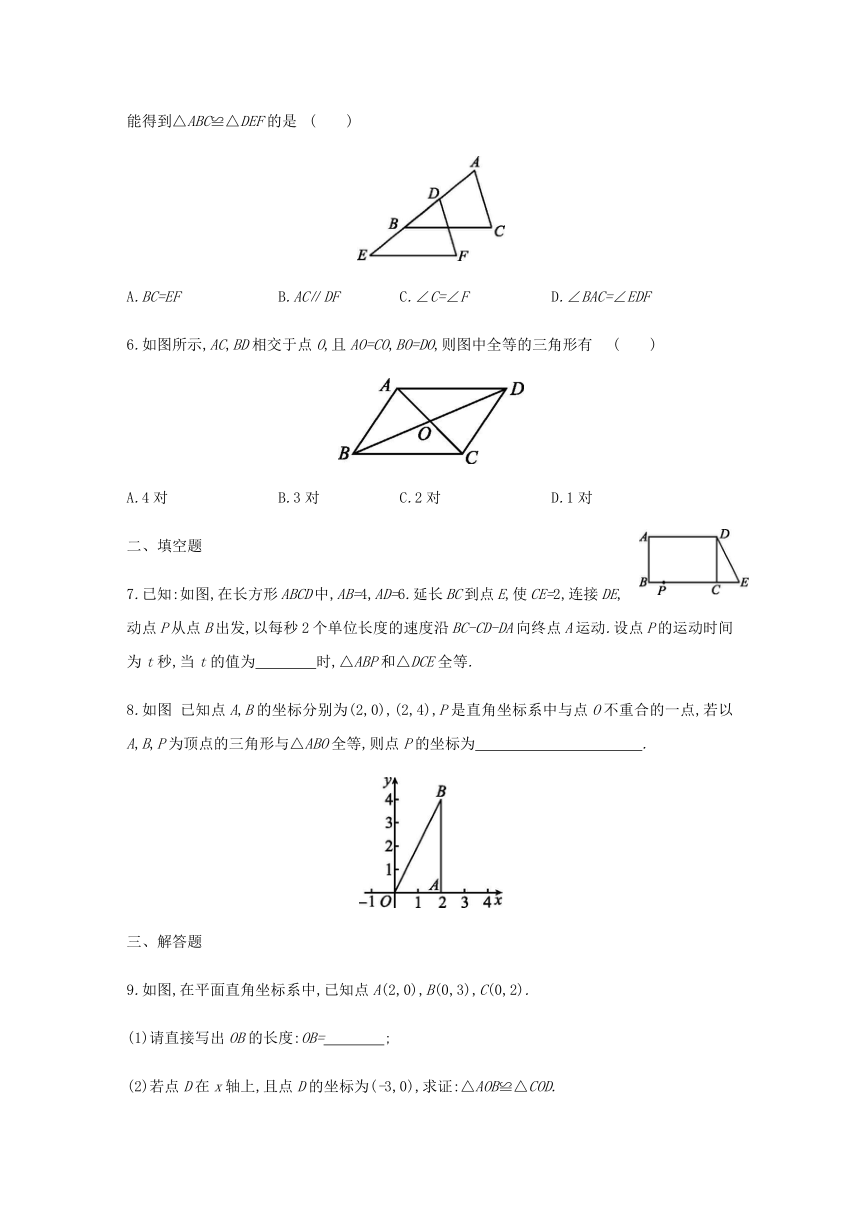
6.如图所示,AC,BD相交于点O,且AO=CO,BO=DO,则图中全等的三角形有
( )
A.4对
B.3对
C.2对
D.1对
填空题
7.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位长度的速度沿BC-CD-DA向终点A运动.设点P的运动时间为t秒,当t的值为 时,△ABP和△DCE全等.?
8.如图
已知点A,B的坐标分别为(2,0),(2,4),P是直角坐标系中与点O不重合的一点,若以A,B,P为顶点的三角形与△ABO全等,则点P的坐标为 .
解答题
9.如图,在平面直角坐标系中,已知点A(2,0),B(0,3),C(0,2).
(1)请直接写出OB的长度:OB= ;?
(2)若点D在x轴上,且点D的坐标为(-3,0),求证:△AOB≌△COD.
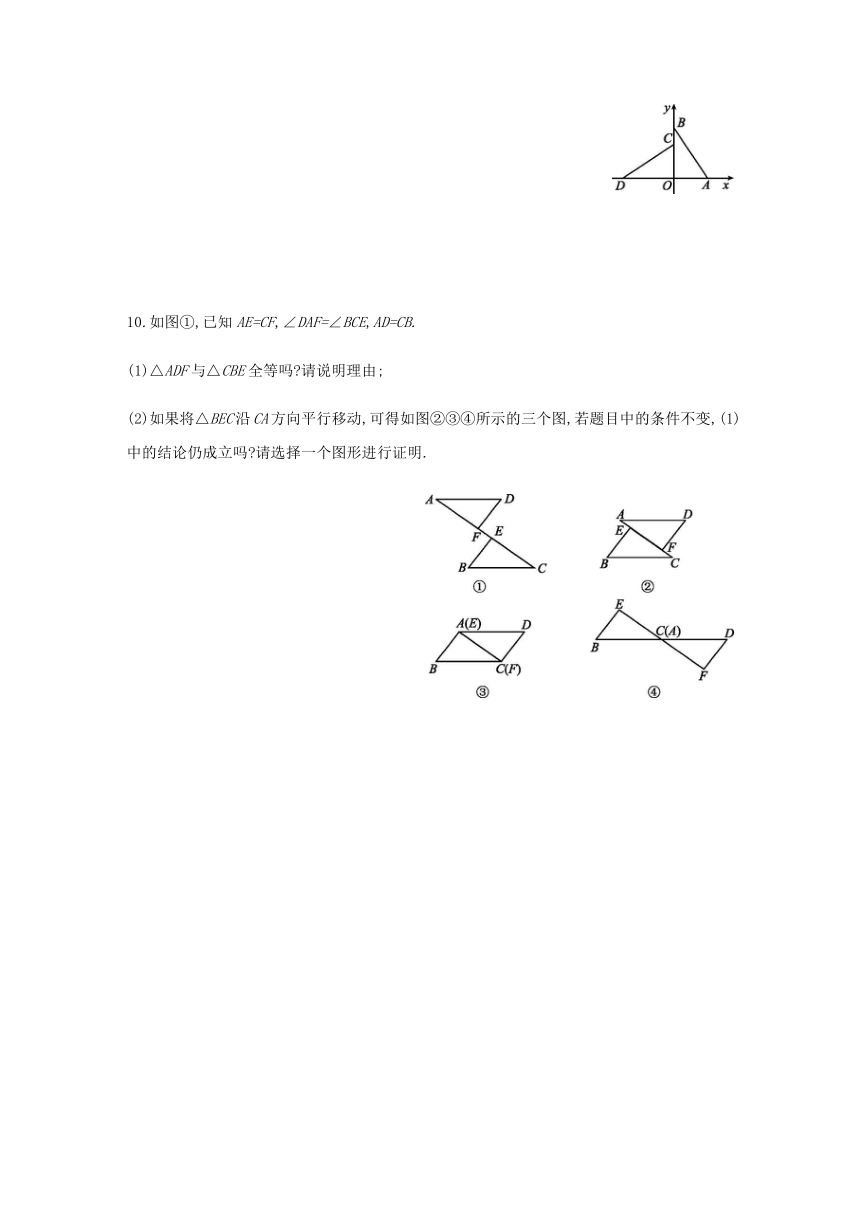
10.如图①,已知AE=CF,∠DAF=∠BCE,AD=CB.
(1)△ADF与△CBE全等吗?请说明理由;
(2)如果将△BEC沿CA方向平行移动,可得如图②③④所示的三个图,若题目中的条件不变,(1)中的结论仍成立吗?请选择一个图形进行证明.
11.如图,在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.
12.(1)如图①,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,求证:EF=BE+DF;
(2)如图②,将(1)中的条件“∠B=∠D=90°”改为“∠B+∠D=180°”,其他条件都不变,(1)中的结论是否仍然成立?(不必给出证明过程)
(3)如图③,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E,F分别是边BC,CD延长线上的点,且∠EAF=∠BAD,请直接写出EF,BE,DF三者之间的数量关系.
答案
1.C 2.B 3.B
4.A 5.C 6.A
7.1或7
8.(0,4)或(4,0)或(4,4)
9.解:(1)3
(2)证明:∵点A(2,0),B(0,3),C(0,2),D(-3,0),
∴OC=OA=2,OB=OD=3.
在△AOB和△COD中,
∴△AOB≌△COD(SAS).
10.解:(1)全等.
理由:∵AE=CF,
∴AE-EF=CF-EF,即AF=CE.
在△ADF和△CBE中,
∴△ADF≌△CBE.
(2)仍成立.如选择题图②证明:
∵AE=CF,∴AE+EF=CF+EF,
即AF=CE.
在△ADF和△CBE中,
∴△ADF≌△CBE.
11.证明:在△ABF和△ACE中,
∴△ABF≌△ACE.∴BF=CE.
∵AB=AC,AE=AF,∴BE=CF.
在△EBC和△FCB中,
∴△EBC≌△FCB.
12.解:(1)证明:如图,延长EB到点G,使BG=DF,连接AG.
∵∠ABC=90°,∴∠ABG=90°.
在△ABG和△ADF中,
∴△ABG≌△ADF.∴AG=AF,∠1=∠2.
∴∠1+∠3=∠2+∠3=∠BAD=∠EAF,即∠EAG=∠EAF.
在△AEG和△AEF中,
∴△AEG≌△AEF.∴EG=EF.
∵EG=BE+BG,∴EF=BE+DF.
(2)结论EF=BE+DF仍然成立.
(3)EF=BE-DF.
三角形全等的判定(二)(SAS)
一、选择题
1.根据下列已知条件,能画出唯一△ABC的是
( )
A.AB=3,BC=4,AC=7
B.AB=4,BC=3,∠C=30°
C.BC=7,AB=3,∠B=45°
D.∠C=90°,AB=4
2.如图,a,b,c分别表示△ABC的三边长,则图中的三角形与△ABC一定全等的是
( )
3.如图,AC和BD相交于点O.若OA=OD,则用“SAS”证明△AOB≌△DOC还需添加的条件是
( )
A.AB=DC
B.OB=OC
C.∠C=∠D
D.∠A=∠D
4.如图,已知AB=AD,∠1=∠2=50°,∠D=100°,那么∠ACB的度数为
( )
A.30°
B.40°
C.50°
D.60°
5.如图,已知点A,D,B,E在同一条直线上,且AD=BE,AC=DF,补充下列其中一个条件后,不一定能得到△ABC≌△DEF的是
( )
A.BC=EF
B.AC∥DF
C.∠C=∠F
D.∠BAC=∠EDF
6.如图所示,AC,BD相交于点O,且AO=CO,BO=DO,则图中全等的三角形有
( )
A.4对
B.3对
C.2对
D.1对
填空题
7.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位长度的速度沿BC-CD-DA向终点A运动.设点P的运动时间为t秒,当t的值为 时,△ABP和△DCE全等.?
8.如图
已知点A,B的坐标分别为(2,0),(2,4),P是直角坐标系中与点O不重合的一点,若以A,B,P为顶点的三角形与△ABO全等,则点P的坐标为 .
解答题
9.如图,在平面直角坐标系中,已知点A(2,0),B(0,3),C(0,2).
(1)请直接写出OB的长度:OB= ;?
(2)若点D在x轴上,且点D的坐标为(-3,0),求证:△AOB≌△COD.
10.如图①,已知AE=CF,∠DAF=∠BCE,AD=CB.
(1)△ADF与△CBE全等吗?请说明理由;
(2)如果将△BEC沿CA方向平行移动,可得如图②③④所示的三个图,若题目中的条件不变,(1)中的结论仍成立吗?请选择一个图形进行证明.
11.如图,在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.
12.(1)如图①,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,求证:EF=BE+DF;
(2)如图②,将(1)中的条件“∠B=∠D=90°”改为“∠B+∠D=180°”,其他条件都不变,(1)中的结论是否仍然成立?(不必给出证明过程)
(3)如图③,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E,F分别是边BC,CD延长线上的点,且∠EAF=∠BAD,请直接写出EF,BE,DF三者之间的数量关系.
答案
1.C 2.B 3.B
4.A 5.C 6.A
7.1或7
8.(0,4)或(4,0)或(4,4)
9.解:(1)3
(2)证明:∵点A(2,0),B(0,3),C(0,2),D(-3,0),
∴OC=OA=2,OB=OD=3.
在△AOB和△COD中,
∴△AOB≌△COD(SAS).
10.解:(1)全等.
理由:∵AE=CF,
∴AE-EF=CF-EF,即AF=CE.
在△ADF和△CBE中,
∴△ADF≌△CBE.
(2)仍成立.如选择题图②证明:
∵AE=CF,∴AE+EF=CF+EF,
即AF=CE.
在△ADF和△CBE中,
∴△ADF≌△CBE.
11.证明:在△ABF和△ACE中,
∴△ABF≌△ACE.∴BF=CE.
∵AB=AC,AE=AF,∴BE=CF.
在△EBC和△FCB中,
∴△EBC≌△FCB.
12.解:(1)证明:如图,延长EB到点G,使BG=DF,连接AG.
∵∠ABC=90°,∴∠ABG=90°.
在△ABG和△ADF中,
∴△ABG≌△ADF.∴AG=AF,∠1=∠2.
∴∠1+∠3=∠2+∠3=∠BAD=∠EAF,即∠EAG=∠EAF.
在△AEG和△AEF中,
∴△AEG≌△AEF.∴EG=EF.
∵EG=BE+BG,∴EF=BE+DF.
(2)结论EF=BE+DF仍然成立.
(3)EF=BE-DF.
