物理:3.3《几种常见的磁场》精品学案(人教版选修3-1)
文档属性
| 名称 | 物理:3.3《几种常见的磁场》精品学案(人教版选修3-1) |

|
|
| 格式 | zip | ||
| 文件大小 | 139.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2011-08-17 00:00:00 | ||
图片预览



文档简介
第3节 几种常见的磁场
要点一 利用安培定则分析电流的磁场的方法
1.分清“因”和“果”:在判定直线电流的磁场方向时,大拇指指“原因”——电流方向,四指指“结果”——磁场绕向;在判定环形电流的磁场方向时,四指指“原因”——电流绕向,大拇指指“结果”——环内沿中心轴线的磁感线方向.
2.优先采用整体法:一个任意形状的环形电流(如三角形、矩形、圆形)的磁场,都可以视为若干或无数个很短的直线电流的磁场叠加而成,从而可分段进行判定.这种隔离法的判定结果,虽然与视为环形电流的整体法一致,但在步骤上却麻烦多了.
要点二 磁通量的理解
1.磁通量的定义
公式Φ=BS中的B应是匀强磁场的磁感应强度,S是与磁场方向垂直的面积,因此,可以理解为Φ=BS⊥.如果平面与磁场方向不垂直,应把面积S投影到与磁场垂直的方向上,求出投影面积S⊥,代入到Φ=BS⊥中计算,应避免硬套公式Φ=BSsin θ或Φ=BScos θ.
2.磁通量的变化
一般有下列三种情况:
(1)磁感应强度B不变,有效面积S变化,则ΔΦ=Φt-Φ0=B·ΔS.
(2)磁感应强度B变化,磁感线穿过的有效面积S不变,则穿过回路中的磁通量的变化是:ΔΦ=Φt-Φ0=ΔB·S.
(3)磁感应强度B和有效面积S同时发生变化的情况,则ΔΦ=Φt-Φ0.
特别提醒 ①平面S与磁场方向不垂直时,要把面积S投影到与磁场垂直的方向上,即求出有效面积.
②可以把磁通量理解为穿过面积S的磁感线的净条数.相反方向穿过面积S的磁感线可以互相抵消.
③当磁感应强度和有效面积同时发生变化时,ΔΦ=Φt-Φ0,而不能用ΔΦ=ΔB·ΔS计算.
1.电场线与磁感线有哪些异同?
电场线 磁感线
相点 引入目的 形象描述场而引入的假想线,实际不存在
疏密 场的强弱
切线方向 场的方向
相交 不能相交(电场中无电荷空间不相交)
不同点 起始于正电荷,终止于负电荷 闭合曲线
特别提醒 (1)从电场、磁场的概念理解两种场线的相似点:矢量性——线的切线,强弱——线的疏密,方向的唯一性——空间任一点场线不相交.
(2)从两种场线的区别理解两种场的区别:
电场线——电荷有正负——电场线有始终
磁感线——N、S极不可分离——磁感线闭合
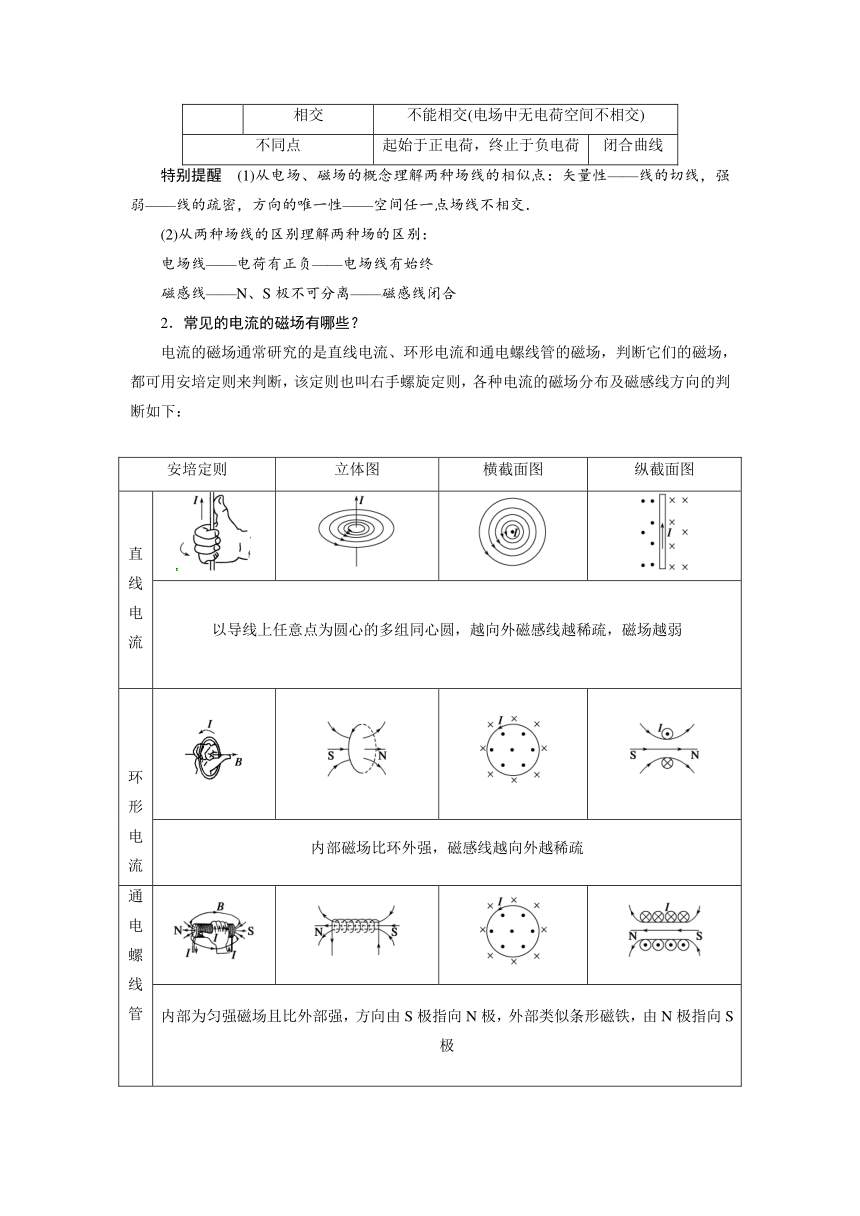
2.常见的电流的磁场有哪些?
电流的磁场通常研究的是直线电流、环形电流和通电螺线管的磁场,判断它们的磁场,都可用安培定则来判断,该定则也叫右手螺旋定则,各种电流的磁场分布及磁感线方向的判断如下:
安培定则 立体图 横截面图 纵截面图
直线电流
以导线上任意点为圆心的多组同心圆,越向外磁感线越稀疏,磁场越弱
环形电流
内部磁场比环外强,磁感线越向外越稀疏
通电螺线管
内部为匀强磁场且比外部强,方向由S极指向N极,外部类似条形磁铁,由N极指向S极
一、磁感线的理解
【例1】 关于磁感线,下列说法中正确的是( )
A.两条磁感线的空隙处一定不存在磁场
B.磁感线总是从N极到S极
C.磁感线上每一点的切线方向都跟该点的磁场方向一致
D.两个磁场叠加的区域,磁感线就可能相交
答案 C
解析 磁感线是为了形象地描绘磁场而假设的一组有方向的曲线,曲线上每一点的切线方向都表示该点的磁场方向,曲线疏密表示磁场强弱,所以C正确,A不正确.在磁铁外部磁感线从N极到S极,内部从S极到N极.磁感线不相交,所以B、D不正确.
二、几种电流的磁场
【例2】 如图3-3-2所示,螺线管、蹄形铁芯、环形导线三者相距较远,当开关闭合后关于小磁针N极(黑色的一端)的指向错误的是( )
图3-3-2
A.小磁针a的N极指向正确
B.小磁针b的N极指向正确
C.小磁针c的N极指向正确
D.小磁针d的N极指向正确
答案 A
解析 小磁针静止时N极的指向为该处的磁场方向,即磁感线的切线方向.根据安培定则,蹄形铁芯被磁化后右端为N极,左端为S极,小磁针c指向正确;通电螺线管的磁场分布和条形磁铁相似,内部磁场向左,外部磁场向右,所以小磁针b指向正确,小磁针a指向错误;环形电流形成的磁场左侧应为S极,故d的指向正确.在运用安培定则判定直线电流和环形电流的磁场时应分清“因”和“果”,在判定直线电流的磁场方向时,大拇指指“原因”——电流方向,四指指“结果”——磁场绕向;在判定环形电流磁场方向时,四指指“原因”——电流绕向,大拇指指“结果”——环内沿中心轴线的磁感线方向.
1.关于磁场和磁感线的描述,下列说法中正确的是( )
A.磁极之间的相互作用是通过磁场发生的,磁场和电场一样,也是一种客观存在的特殊物质
B.磁感线可以形象地描述各磁场的强弱和方向,它每一点的切线方向都和小磁针放在该点静止时北极所指的方向一致
C.磁感线总是从磁铁的N极出发,到S极终止的
D.磁感线可以用细铁屑来显示,因而是真实存在的
答案 AB
解析 磁感线是为了形象描述磁场而假设的一簇有方向的闭合的曲线,实际上并不存在,所以C、D不正确;磁场是客观存在的特殊物质,所以A正确;磁感线上每一点切线方向表示该点磁场方向,磁感线疏密表示该点磁场的强弱,小磁针静止时北极指向、北极受力方向均为磁场方向,所以B正确.
2.磁铁在高温下或者受到敲击时会失去磁性,根据安培分子电流假说,其原因是( )
A.分子电流消失
B.分子电流取向变得大致相同
C.分子电流取向变得杂乱
D.分子电流减弱
答案 C
解析 根据安培的分子电流假说,当分子电流取向变得大致相同时,对外显示磁性;当温度升高或者受到敲击时,分子发生运动,分子电流取向变得杂乱无序,对外不能显示磁性.安培的分子电流假说不仅解决了磁现象的电本质,同时对我们的生活生产也很有指导作用,让我们知道了如何充磁、如何退磁.
3.放在通电螺线管里面的小磁针保持静止时,N极的指向是怎样的?两位同学的回答相反,甲说,小磁针的位置如图3-3-3甲所示,因为管内的磁感线方向向右,所以小磁针的N极指向右方.乙说,小磁针的位置如图乙所示,他的理由是通电螺线管的N极在右侧,根据异名磁极相互吸引可知,小磁针的S极指向右方.你的看法是怎样的?他们谁的答案错了?
图3-3-3
答案 磁场中保持静止的小磁针,它的N极一定指向磁感线的方向,甲回答的是对的,乙的答案错了.
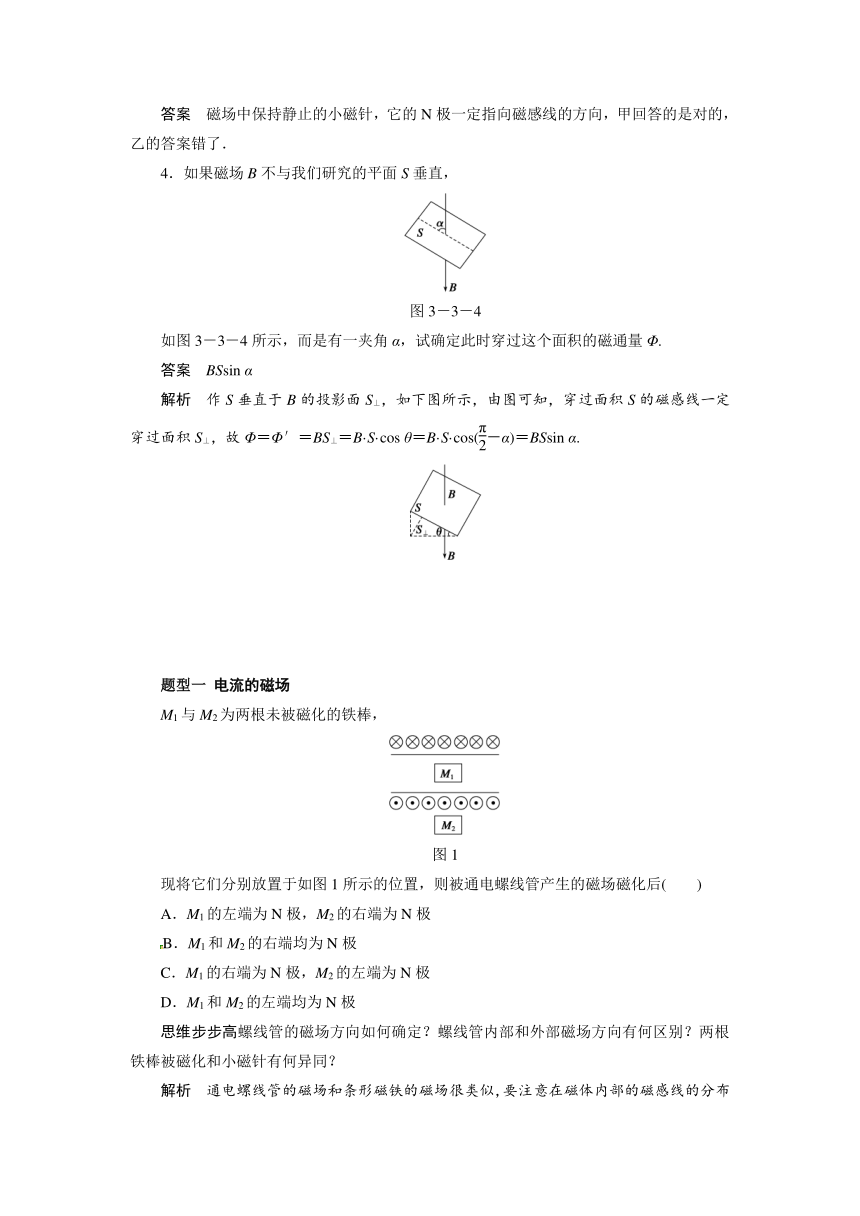
4.如果磁场B不与我们研究的平面S垂直,
图3-3-4
如图3-3-4所示,而是有一夹角α,试确定此时穿过这个面积的磁通量Φ.
答案 BSsin α
解析 作S垂直于B的投影面S⊥,如下图所示,由图可知,穿过面积S的磁感线一定穿过面积S⊥,故Φ=Φ′=BS⊥=B·S·cos θ=B·S·cos(-α)=BSsin α.
题型一 电流的磁场
M1与M2为两根未被磁化的铁棒,
图1
现将它们分别放置于如图1所示的位置,则被通电螺线管产生的磁场磁化后( )
A.M1的左端为N极,M2的右端为N极
B.M1和M2的右端均为N极
C.M1的右端为N极,M2的左端为N极
D.M1和M2的左端均为N极
思维步步高螺线管的磁场方向如何确定?螺线管内部和外部磁场方向有何区别?两根铁棒被磁化和小磁针有何异同?
解析 通电螺线管的磁场和条形磁铁的磁场很类似,要注意在磁体内部的磁感线的分布应该是从S极指向N极的.
答案 A
拓展探究如图2所示,
图2
小磁针静止在通电螺线管的旁边,请在图上标出电流的方向.
答案 见解析
解析 根据通电螺线管的磁场与小磁针的相互作用情况可以判断:螺线管的右边应该是S极.再根据安培定则,右手握住螺线管,
大拇指指螺线管的N极,其余四指的方向就是通电螺线管中的电流方向,即电流从右边流入,左边流出,如右图所示.
通电导线的磁场有以下几种常见的情况:①通电直导线的磁场,大拇指的方向为电流的方向,四指的指向为磁场的方向.②通电螺线管的磁场,四指的环绕方向是电流的方向,大拇指的指向是螺线管内部的磁感线的方向.③通电线圈相当于单匝的通电螺线管.
题型二 磁通量问题
如图3所示,
图3
一环形线圈沿条形磁铁的轴线,从磁铁N极的左侧A点运动到磁铁S极的右侧B点,A、B两点关于磁铁的中心对称,则在此过程中,穿过环形线圈的磁通量将( )
A.先增大,后减小
B.先减小,后增大
C.先增大,后减小、再增大,再减小
D.先减小,后增大、再减小,再增大
思维步步高A处的磁场方向向哪?从A运动到磁铁N极过程中磁场的强弱怎样变化?在穿过磁铁的过程中穿过线圈的磁感线方向向哪?从S极向B运动的过程中,磁场强弱怎样变化?磁通量怎样变化?
解析 在磁铁内部磁感应强度最大,磁感线条数最多,在A端和B端,磁铁的部分磁感线通过线圈,而在磁铁中间,磁铁的全部磁感线通过线圈,只在外部有少量的抵消,因此穿过线圈的磁通量先增大后减小.
答案 A
拓展探究条形磁铁竖直放置,
图4
闭合圆环水平放置,条形磁铁中心线穿过圆环中心,如图4所示,若圆环为弹性环,其形状由Ⅰ扩大到Ⅱ,那么圆环内磁通量的变化的情况是( )
A.磁通量增大 B.磁通量减小
C.磁通量不变 D.条件不足,无法确定
答案 B
解析 磁感线是闭合曲线,磁铁内部是由S极到N极,而外部是由N极回到S极,而磁通量是穿过某个面的磁感线的净条数,故B正确.
磁通量问题要注意以下几个问题:①磁通量的定义式Φ=BS中的面积为有效面积,是线圈平面在垂直于磁感线方向的投影.②当磁铁穿过线圈时,在磁铁内部的磁感线是从S极指向N极的.
一、选择题
1.如图5所示,
图5
带负电的金属环绕轴OO′以角速度ω匀速旋转,在环左侧轴线上的小磁针最后平衡的位置是( )
A.N极竖直向上
B.N极竖直向下
C.N极沿轴线向左
D.N极沿轴线向右
答案 D
2.关于磁现象的电本质,正确的说法是( )
①一切磁现象都起源于电流或运动电荷,一切磁作用都是电流或运动电荷之间通过磁场而发生的相互作用 ②除永久磁铁外,一切磁场都是由运动电荷或电流产生的 ③根据安培的分子电流假说,在外界磁场作用下,物体内部分子电流取向变得大致相同时,物体就被磁化,两端形成磁极 ④磁就是电,电就是磁,有磁必有电,有电必有磁
A.②③④ B.②④ C.①③ D.①②③
答案 C
解析 ②错误在于永久磁体之所以显磁性的原因是内部分子电流规律分布.④错误的原因是静止的电荷周围就没有磁场.只有运动电荷才能产生磁场.
图6
3.如图6所示,圆环上带有大量的负电荷,当圆环沿顺时针方向转动时,a、b、c三枚小磁针都要发生转动,以下说法正确的是( )
A.a、b、c的N极都向纸里转
B.b的N极向纸外转,而a、c的N极向纸里转
C.b、c的N极都向纸里转,而a的N极向纸外转
D.b的N极向纸里转,而a、c的N极向纸外转
答案 B
4.磁体之间的相互作用是通过磁场发生的.对磁场认识正确的是( )
A.磁感线有可能出现相交的情况
B.磁感线总是由N极出发指向S极
C.某点磁场的方向与放在该点的小磁针静止时N极所指方向一致
D.若在某区域内通电导线不受磁场力的作用,则该区域的磁感应强度一定为零
答案 C
解析 根据磁感线的特点:(1)磁感线在空间内不能相交;(2)磁感线是闭合曲线,在磁体外部由N极指向S极,在磁体内部由S极指向N极;(3)磁感线的切线方向表示磁场的方向(小磁针静止时N极指向).可判断选项A、B错误,C正确.通电导线在磁场中是否受力与导线在磁场中的放置方式有关,故D错.
5.
图7
南极考察经常就南极特殊的地理位置进行科学测量.“雪龙号”考察队员一次实验如下:在地球南极附近用弹簧测力计竖直悬挂一未通电螺线管,如图7所示.下列说法正确的是( )
A.若将a端接电源正极,b端接电源负极,则弹簧测力计示数将减小
B.若将a端接电源正极,b端接电源负极,则弹簧测力计示数将增大
C.若将b端接电源正极,a端接电源负极,则弹簧测力计示数将增大
D.不论螺线管通电情况如何,弹簧测力计示数均不变
答案 AC
解析 在地球南极附近即为地磁N极,螺线管相当于一条形磁铁,根据右手螺旋定则判断出“条形磁铁”的极性.
6.如图8所示,
图8
在条形磁铁外套有A、B两个大小不同的圆环,穿过A环的磁通量ΦA与穿过B环的磁通量ΦB相比较( )
A.ΦA>ΦB
B.ΦA<ΦB
C.ΦA=ΦB
D.不能确定
答案 A
解析 Φ=Φ内-Φ外,对A、B两环Φ内相同,而B的Φ外大于A的,所以ΦA>ΦB.
7.如图9所示,
图9
螺线管中通有电流,如果在图中的a、b、c三个位置上各放一个小磁针,其中a在螺线管内部,则( )
A.放在a处的小磁针的N极向左
B.放在b处的小磁针的N极向右
C.放在c处的小磁针的S极向右
D.放在a处的小磁针的N极向右
答案 BD
解析
由安培定则,通电螺线管的磁场如右图所示,右端为N极,左端为S极,在a点磁场方向向右,则小磁针在a点时,N极向右,则A项错,D项对;在b点磁场方向向右,则磁针在b点时,N极向右,则B项正确;在c点,磁场方向向右,则磁针在c点时,N极向右,S极向左,则C项错.
二、计算论述题
8.如图10所示,
图10
面积是0.5 m2的矩形导线圈处于磁感应强度为20 T的匀强磁场中,线圈平面与磁场垂直,如图中Ⅰ位置,则穿过该线圈的磁通量是多少?若线圈平面与磁场方向夹角为60°,如图Ⅱ位置,则穿过该线圈的磁通量又是多少?
答案 10 Wb 8.66 Wb
解析 已知S=0.5 m2,B=20 T
(1)因为线圈平面与磁场垂直,所以
ΦⅠ=BS=20×0.5 Wb=10 Wb
(2)因为线圈平面与磁场方向夹角为60°,所以
ΦⅡ=BSsin θ=20×0.5×sin 60°Wb=8.66 Wb.
9.如图11所示,
图11
一根通电直导线垂直放在磁感应强度B=1 T水平向右的匀强磁场中,以导线截面的中心为圆心,半径为r的圆周上有a、b、c、d四点,已知a点的实际磁感应强度为零,则b、c、d三点的磁感应强度分别是多少?方向如何?
答案 Bb= T,与水平方向成45°斜向右上
Bc=2 T,方向水平向右
Bd= T,与水平方向成45°斜向右下
解析
a、b、c、d各点的磁场均为匀强磁场与电流的磁场的叠加,并且电流在这四点所产生的磁感应强度B′大小相等,由于Ba=0,则B′=B=1 T,由安培定则可知,导线中电流方向向外,则在b、c、d电流的磁场如右图所示.
,θ=45°,即Bb与水平方向成45°斜向右上
Bc=B′+B=2 T,方向水平向右
,α=45°,即Bd与水平方向成45°斜向右下
10.如图12所示,
图12
有一个垂直于纸面向里的匀强磁场,磁感应强度为B=0.8 T,磁场有明显的圆形边界,圆心为O,半径为1 cm.现于纸面内先后放上圆线圈,圆心均在O处,A线圈半径为1 cm,1匝;B线圈半径为2 cm,1匝;C线圈半径为0.5 cm,1匝.问:
(1)在B减为0.4 T的过程中,A和B中磁通量各改变多少?
(2)当磁场方向转过30°角的过程中,C中的磁通量改变多少?
答案 (1)1.256×10-4 Wb 1.256×10-4 Wb
(2)8.4×10-6 Wb
解析 (1)设圆形磁场区域的半径为R
对线圈A Φ1=B1πR2,Φ2=B2πR2
磁通量的改变量:ΔΦ=|Φ2-Φ1|
=(0.8-0.4)×3.14×(10-2)2 Wb=1.256×10-4 Wb
对B ΔΦ=|Φ2-Φ1|
=(0.8-0.4)×3.14×(10-2)2 Wb=1.256×10-4 Wb
(2)对线圈C:设C线圈的半径为r
Φ1=Bπr2sin θ1,Φ2=Bπr2sin θ2
磁通量的改变量:
ΔΦ=|Φ2-Φ1|=Bπr2(sin 90°-sin 60°)=8.4×10-6 Wb
要点一 利用安培定则分析电流的磁场的方法
1.分清“因”和“果”:在判定直线电流的磁场方向时,大拇指指“原因”——电流方向,四指指“结果”——磁场绕向;在判定环形电流的磁场方向时,四指指“原因”——电流绕向,大拇指指“结果”——环内沿中心轴线的磁感线方向.
2.优先采用整体法:一个任意形状的环形电流(如三角形、矩形、圆形)的磁场,都可以视为若干或无数个很短的直线电流的磁场叠加而成,从而可分段进行判定.这种隔离法的判定结果,虽然与视为环形电流的整体法一致,但在步骤上却麻烦多了.
要点二 磁通量的理解
1.磁通量的定义
公式Φ=BS中的B应是匀强磁场的磁感应强度,S是与磁场方向垂直的面积,因此,可以理解为Φ=BS⊥.如果平面与磁场方向不垂直,应把面积S投影到与磁场垂直的方向上,求出投影面积S⊥,代入到Φ=BS⊥中计算,应避免硬套公式Φ=BSsin θ或Φ=BScos θ.
2.磁通量的变化
一般有下列三种情况:
(1)磁感应强度B不变,有效面积S变化,则ΔΦ=Φt-Φ0=B·ΔS.
(2)磁感应强度B变化,磁感线穿过的有效面积S不变,则穿过回路中的磁通量的变化是:ΔΦ=Φt-Φ0=ΔB·S.
(3)磁感应强度B和有效面积S同时发生变化的情况,则ΔΦ=Φt-Φ0.
特别提醒 ①平面S与磁场方向不垂直时,要把面积S投影到与磁场垂直的方向上,即求出有效面积.
②可以把磁通量理解为穿过面积S的磁感线的净条数.相反方向穿过面积S的磁感线可以互相抵消.
③当磁感应强度和有效面积同时发生变化时,ΔΦ=Φt-Φ0,而不能用ΔΦ=ΔB·ΔS计算.
1.电场线与磁感线有哪些异同?
电场线 磁感线
相点 引入目的 形象描述场而引入的假想线,实际不存在
疏密 场的强弱
切线方向 场的方向
相交 不能相交(电场中无电荷空间不相交)
不同点 起始于正电荷,终止于负电荷 闭合曲线
特别提醒 (1)从电场、磁场的概念理解两种场线的相似点:矢量性——线的切线,强弱——线的疏密,方向的唯一性——空间任一点场线不相交.
(2)从两种场线的区别理解两种场的区别:
电场线——电荷有正负——电场线有始终
磁感线——N、S极不可分离——磁感线闭合
2.常见的电流的磁场有哪些?
电流的磁场通常研究的是直线电流、环形电流和通电螺线管的磁场,判断它们的磁场,都可用安培定则来判断,该定则也叫右手螺旋定则,各种电流的磁场分布及磁感线方向的判断如下:
安培定则 立体图 横截面图 纵截面图
直线电流
以导线上任意点为圆心的多组同心圆,越向外磁感线越稀疏,磁场越弱
环形电流
内部磁场比环外强,磁感线越向外越稀疏
通电螺线管
内部为匀强磁场且比外部强,方向由S极指向N极,外部类似条形磁铁,由N极指向S极
一、磁感线的理解
【例1】 关于磁感线,下列说法中正确的是( )
A.两条磁感线的空隙处一定不存在磁场
B.磁感线总是从N极到S极
C.磁感线上每一点的切线方向都跟该点的磁场方向一致
D.两个磁场叠加的区域,磁感线就可能相交
答案 C
解析 磁感线是为了形象地描绘磁场而假设的一组有方向的曲线,曲线上每一点的切线方向都表示该点的磁场方向,曲线疏密表示磁场强弱,所以C正确,A不正确.在磁铁外部磁感线从N极到S极,内部从S极到N极.磁感线不相交,所以B、D不正确.
二、几种电流的磁场
【例2】 如图3-3-2所示,螺线管、蹄形铁芯、环形导线三者相距较远,当开关闭合后关于小磁针N极(黑色的一端)的指向错误的是( )
图3-3-2
A.小磁针a的N极指向正确
B.小磁针b的N极指向正确
C.小磁针c的N极指向正确
D.小磁针d的N极指向正确
答案 A
解析 小磁针静止时N极的指向为该处的磁场方向,即磁感线的切线方向.根据安培定则,蹄形铁芯被磁化后右端为N极,左端为S极,小磁针c指向正确;通电螺线管的磁场分布和条形磁铁相似,内部磁场向左,外部磁场向右,所以小磁针b指向正确,小磁针a指向错误;环形电流形成的磁场左侧应为S极,故d的指向正确.在运用安培定则判定直线电流和环形电流的磁场时应分清“因”和“果”,在判定直线电流的磁场方向时,大拇指指“原因”——电流方向,四指指“结果”——磁场绕向;在判定环形电流磁场方向时,四指指“原因”——电流绕向,大拇指指“结果”——环内沿中心轴线的磁感线方向.
1.关于磁场和磁感线的描述,下列说法中正确的是( )
A.磁极之间的相互作用是通过磁场发生的,磁场和电场一样,也是一种客观存在的特殊物质
B.磁感线可以形象地描述各磁场的强弱和方向,它每一点的切线方向都和小磁针放在该点静止时北极所指的方向一致
C.磁感线总是从磁铁的N极出发,到S极终止的
D.磁感线可以用细铁屑来显示,因而是真实存在的
答案 AB
解析 磁感线是为了形象描述磁场而假设的一簇有方向的闭合的曲线,实际上并不存在,所以C、D不正确;磁场是客观存在的特殊物质,所以A正确;磁感线上每一点切线方向表示该点磁场方向,磁感线疏密表示该点磁场的强弱,小磁针静止时北极指向、北极受力方向均为磁场方向,所以B正确.
2.磁铁在高温下或者受到敲击时会失去磁性,根据安培分子电流假说,其原因是( )
A.分子电流消失
B.分子电流取向变得大致相同
C.分子电流取向变得杂乱
D.分子电流减弱
答案 C
解析 根据安培的分子电流假说,当分子电流取向变得大致相同时,对外显示磁性;当温度升高或者受到敲击时,分子发生运动,分子电流取向变得杂乱无序,对外不能显示磁性.安培的分子电流假说不仅解决了磁现象的电本质,同时对我们的生活生产也很有指导作用,让我们知道了如何充磁、如何退磁.
3.放在通电螺线管里面的小磁针保持静止时,N极的指向是怎样的?两位同学的回答相反,甲说,小磁针的位置如图3-3-3甲所示,因为管内的磁感线方向向右,所以小磁针的N极指向右方.乙说,小磁针的位置如图乙所示,他的理由是通电螺线管的N极在右侧,根据异名磁极相互吸引可知,小磁针的S极指向右方.你的看法是怎样的?他们谁的答案错了?
图3-3-3
答案 磁场中保持静止的小磁针,它的N极一定指向磁感线的方向,甲回答的是对的,乙的答案错了.
4.如果磁场B不与我们研究的平面S垂直,
图3-3-4
如图3-3-4所示,而是有一夹角α,试确定此时穿过这个面积的磁通量Φ.
答案 BSsin α
解析 作S垂直于B的投影面S⊥,如下图所示,由图可知,穿过面积S的磁感线一定穿过面积S⊥,故Φ=Φ′=BS⊥=B·S·cos θ=B·S·cos(-α)=BSsin α.
题型一 电流的磁场
M1与M2为两根未被磁化的铁棒,
图1
现将它们分别放置于如图1所示的位置,则被通电螺线管产生的磁场磁化后( )
A.M1的左端为N极,M2的右端为N极
B.M1和M2的右端均为N极
C.M1的右端为N极,M2的左端为N极
D.M1和M2的左端均为N极
思维步步高螺线管的磁场方向如何确定?螺线管内部和外部磁场方向有何区别?两根铁棒被磁化和小磁针有何异同?
解析 通电螺线管的磁场和条形磁铁的磁场很类似,要注意在磁体内部的磁感线的分布应该是从S极指向N极的.
答案 A
拓展探究如图2所示,
图2
小磁针静止在通电螺线管的旁边,请在图上标出电流的方向.
答案 见解析
解析 根据通电螺线管的磁场与小磁针的相互作用情况可以判断:螺线管的右边应该是S极.再根据安培定则,右手握住螺线管,
大拇指指螺线管的N极,其余四指的方向就是通电螺线管中的电流方向,即电流从右边流入,左边流出,如右图所示.
通电导线的磁场有以下几种常见的情况:①通电直导线的磁场,大拇指的方向为电流的方向,四指的指向为磁场的方向.②通电螺线管的磁场,四指的环绕方向是电流的方向,大拇指的指向是螺线管内部的磁感线的方向.③通电线圈相当于单匝的通电螺线管.
题型二 磁通量问题
如图3所示,
图3
一环形线圈沿条形磁铁的轴线,从磁铁N极的左侧A点运动到磁铁S极的右侧B点,A、B两点关于磁铁的中心对称,则在此过程中,穿过环形线圈的磁通量将( )
A.先增大,后减小
B.先减小,后增大
C.先增大,后减小、再增大,再减小
D.先减小,后增大、再减小,再增大
思维步步高A处的磁场方向向哪?从A运动到磁铁N极过程中磁场的强弱怎样变化?在穿过磁铁的过程中穿过线圈的磁感线方向向哪?从S极向B运动的过程中,磁场强弱怎样变化?磁通量怎样变化?
解析 在磁铁内部磁感应强度最大,磁感线条数最多,在A端和B端,磁铁的部分磁感线通过线圈,而在磁铁中间,磁铁的全部磁感线通过线圈,只在外部有少量的抵消,因此穿过线圈的磁通量先增大后减小.
答案 A
拓展探究条形磁铁竖直放置,
图4
闭合圆环水平放置,条形磁铁中心线穿过圆环中心,如图4所示,若圆环为弹性环,其形状由Ⅰ扩大到Ⅱ,那么圆环内磁通量的变化的情况是( )
A.磁通量增大 B.磁通量减小
C.磁通量不变 D.条件不足,无法确定
答案 B
解析 磁感线是闭合曲线,磁铁内部是由S极到N极,而外部是由N极回到S极,而磁通量是穿过某个面的磁感线的净条数,故B正确.
磁通量问题要注意以下几个问题:①磁通量的定义式Φ=BS中的面积为有效面积,是线圈平面在垂直于磁感线方向的投影.②当磁铁穿过线圈时,在磁铁内部的磁感线是从S极指向N极的.
一、选择题
1.如图5所示,
图5
带负电的金属环绕轴OO′以角速度ω匀速旋转,在环左侧轴线上的小磁针最后平衡的位置是( )
A.N极竖直向上
B.N极竖直向下
C.N极沿轴线向左
D.N极沿轴线向右
答案 D
2.关于磁现象的电本质,正确的说法是( )
①一切磁现象都起源于电流或运动电荷,一切磁作用都是电流或运动电荷之间通过磁场而发生的相互作用 ②除永久磁铁外,一切磁场都是由运动电荷或电流产生的 ③根据安培的分子电流假说,在外界磁场作用下,物体内部分子电流取向变得大致相同时,物体就被磁化,两端形成磁极 ④磁就是电,电就是磁,有磁必有电,有电必有磁
A.②③④ B.②④ C.①③ D.①②③
答案 C
解析 ②错误在于永久磁体之所以显磁性的原因是内部分子电流规律分布.④错误的原因是静止的电荷周围就没有磁场.只有运动电荷才能产生磁场.
图6
3.如图6所示,圆环上带有大量的负电荷,当圆环沿顺时针方向转动时,a、b、c三枚小磁针都要发生转动,以下说法正确的是( )
A.a、b、c的N极都向纸里转
B.b的N极向纸外转,而a、c的N极向纸里转
C.b、c的N极都向纸里转,而a的N极向纸外转
D.b的N极向纸里转,而a、c的N极向纸外转
答案 B
4.磁体之间的相互作用是通过磁场发生的.对磁场认识正确的是( )
A.磁感线有可能出现相交的情况
B.磁感线总是由N极出发指向S极
C.某点磁场的方向与放在该点的小磁针静止时N极所指方向一致
D.若在某区域内通电导线不受磁场力的作用,则该区域的磁感应强度一定为零
答案 C
解析 根据磁感线的特点:(1)磁感线在空间内不能相交;(2)磁感线是闭合曲线,在磁体外部由N极指向S极,在磁体内部由S极指向N极;(3)磁感线的切线方向表示磁场的方向(小磁针静止时N极指向).可判断选项A、B错误,C正确.通电导线在磁场中是否受力与导线在磁场中的放置方式有关,故D错.
5.
图7
南极考察经常就南极特殊的地理位置进行科学测量.“雪龙号”考察队员一次实验如下:在地球南极附近用弹簧测力计竖直悬挂一未通电螺线管,如图7所示.下列说法正确的是( )
A.若将a端接电源正极,b端接电源负极,则弹簧测力计示数将减小
B.若将a端接电源正极,b端接电源负极,则弹簧测力计示数将增大
C.若将b端接电源正极,a端接电源负极,则弹簧测力计示数将增大
D.不论螺线管通电情况如何,弹簧测力计示数均不变
答案 AC
解析 在地球南极附近即为地磁N极,螺线管相当于一条形磁铁,根据右手螺旋定则判断出“条形磁铁”的极性.
6.如图8所示,
图8
在条形磁铁外套有A、B两个大小不同的圆环,穿过A环的磁通量ΦA与穿过B环的磁通量ΦB相比较( )
A.ΦA>ΦB
B.ΦA<ΦB
C.ΦA=ΦB
D.不能确定
答案 A
解析 Φ=Φ内-Φ外,对A、B两环Φ内相同,而B的Φ外大于A的,所以ΦA>ΦB.
7.如图9所示,
图9
螺线管中通有电流,如果在图中的a、b、c三个位置上各放一个小磁针,其中a在螺线管内部,则( )
A.放在a处的小磁针的N极向左
B.放在b处的小磁针的N极向右
C.放在c处的小磁针的S极向右
D.放在a处的小磁针的N极向右
答案 BD
解析
由安培定则,通电螺线管的磁场如右图所示,右端为N极,左端为S极,在a点磁场方向向右,则小磁针在a点时,N极向右,则A项错,D项对;在b点磁场方向向右,则磁针在b点时,N极向右,则B项正确;在c点,磁场方向向右,则磁针在c点时,N极向右,S极向左,则C项错.
二、计算论述题
8.如图10所示,
图10
面积是0.5 m2的矩形导线圈处于磁感应强度为20 T的匀强磁场中,线圈平面与磁场垂直,如图中Ⅰ位置,则穿过该线圈的磁通量是多少?若线圈平面与磁场方向夹角为60°,如图Ⅱ位置,则穿过该线圈的磁通量又是多少?
答案 10 Wb 8.66 Wb
解析 已知S=0.5 m2,B=20 T
(1)因为线圈平面与磁场垂直,所以
ΦⅠ=BS=20×0.5 Wb=10 Wb
(2)因为线圈平面与磁场方向夹角为60°,所以
ΦⅡ=BSsin θ=20×0.5×sin 60°Wb=8.66 Wb.
9.如图11所示,
图11
一根通电直导线垂直放在磁感应强度B=1 T水平向右的匀强磁场中,以导线截面的中心为圆心,半径为r的圆周上有a、b、c、d四点,已知a点的实际磁感应强度为零,则b、c、d三点的磁感应强度分别是多少?方向如何?
答案 Bb= T,与水平方向成45°斜向右上
Bc=2 T,方向水平向右
Bd= T,与水平方向成45°斜向右下
解析
a、b、c、d各点的磁场均为匀强磁场与电流的磁场的叠加,并且电流在这四点所产生的磁感应强度B′大小相等,由于Ba=0,则B′=B=1 T,由安培定则可知,导线中电流方向向外,则在b、c、d电流的磁场如右图所示.
,θ=45°,即Bb与水平方向成45°斜向右上
Bc=B′+B=2 T,方向水平向右
,α=45°,即Bd与水平方向成45°斜向右下
10.如图12所示,
图12
有一个垂直于纸面向里的匀强磁场,磁感应强度为B=0.8 T,磁场有明显的圆形边界,圆心为O,半径为1 cm.现于纸面内先后放上圆线圈,圆心均在O处,A线圈半径为1 cm,1匝;B线圈半径为2 cm,1匝;C线圈半径为0.5 cm,1匝.问:
(1)在B减为0.4 T的过程中,A和B中磁通量各改变多少?
(2)当磁场方向转过30°角的过程中,C中的磁通量改变多少?
答案 (1)1.256×10-4 Wb 1.256×10-4 Wb
(2)8.4×10-6 Wb
解析 (1)设圆形磁场区域的半径为R
对线圈A Φ1=B1πR2,Φ2=B2πR2
磁通量的改变量:ΔΦ=|Φ2-Φ1|
=(0.8-0.4)×3.14×(10-2)2 Wb=1.256×10-4 Wb
对B ΔΦ=|Φ2-Φ1|
=(0.8-0.4)×3.14×(10-2)2 Wb=1.256×10-4 Wb
(2)对线圈C:设C线圈的半径为r
Φ1=Bπr2sin θ1,Φ2=Bπr2sin θ2
磁通量的改变量:
ΔΦ=|Φ2-Φ1|=Bπr2(sin 90°-sin 60°)=8.4×10-6 Wb
