《函数应用》单元测试题
图片预览

文档简介
《函数应用》单元测试题
选择题:
1. 函数的零点为 ( )
(A).1或3 (B).-1或3 (C).1或-3 (D).-1或-3
2. 下列函数在区间[1,2]上有零点的是 ( )
3. 下列函数中有两个零点的是 ( )
4. 方程的根的个数为 ( )
(A).0 (B).1 (C).2 (D).3
5. 方程的解的个数是 ( )
(A).0 (B).1 (C).2 (D).与a的取值有关
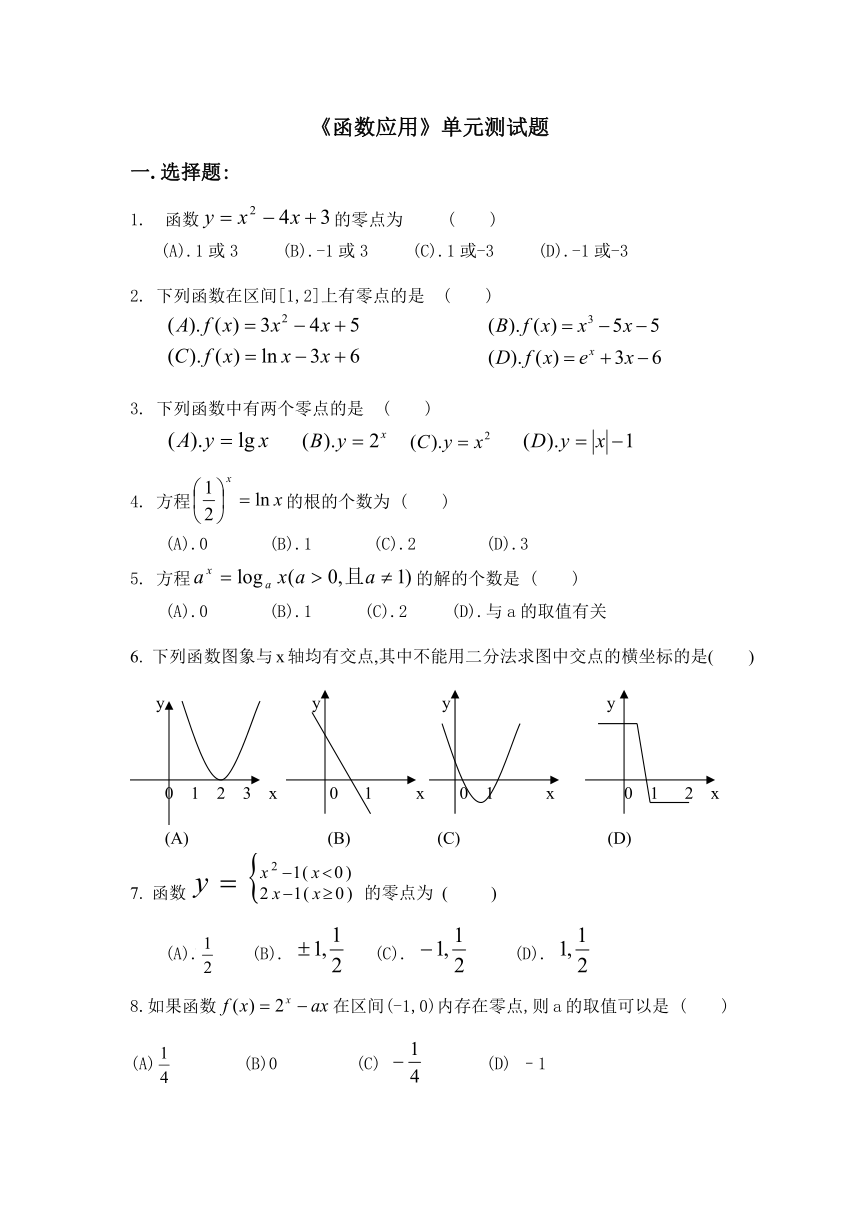
6. 下列函数图象与x轴均有交点,其中不能用二分法求图中交点的横坐标的是( )
y y y y
0 1 2 3 x 0 1 x 0 1 x 0 1 2 x
(A) (B) (C) (D)
7. 函数的零点为 ( )
(A). (B). (C). (D).
8.如果函数在区间(-1,0)内存在零点,则a的取值可以是 ( )
(A) (B)0 (C) (D) –1
填空题:
9.函数在R上的零点有________个.
10.已知函数,若f(x)在R上有一个零点,a=_______;若f(x)在R 上有2个零点,则a的取值范围为______________.
11.方程有两个不等实根,且,则实数k的取值范围为_________.
12.若函数有零点,则实数m的取值范围是___________.
13.已知函数是R上的奇函数,则函数的图象关于_______对称; 若有2005个零点(记为),则_____.
三. 解答题:
14. 已知函数,判断方程在区间[1,1.5]内是否有实数解,如果有,求出一个近似解(精确到0.1).
17. (15分)一种放射性元素,其最初的质量为500g,按每年10%的速度衰减,
(1)求t年后,这种放射性元素的质量m的表达式;
(2)求这种放射性元素的半衰期(精确到0.1年,)
18.(15分)某商店如果将进货为8元的商品按每件10元售出,每天可销售200件,现在采用提高售价,减少进货量的方法增加利润,已知这种商品每涨价0.5元,其销售量就减少10件,问应该将售价定为多少时,才能使所赚利润最大,并求出最大利润.
20.(15分)某市电力公司在电力供大于求时期为了鼓励居民用电,采用分段计费方法计算电费,每月用电不超过100度时,按每度0.57元计费;每月用电超过100度时,其中的100度仍按原标准收费,超过部分按每度0.5元计费.
(1)设每月用电x度,应交电费y元,写出y关于x的函数关系.
(2)小王家第一季度共用了多少度电
月份 1月份 2月份 3月份 合计
缴费金额 76元 63元 45元6角 184元6角
问:小王家第一季度共用了多少度电
参考答案:
一.1-8:A D D B D、A C D
二.9.1; 10.±2, {a|a>2或a<-2}; 11.(0,);
12.(0,1); 13.原点,0
三.14. 1.3;15.(1){x|
选择题:
1. 函数的零点为 ( )
(A).1或3 (B).-1或3 (C).1或-3 (D).-1或-3
2. 下列函数在区间[1,2]上有零点的是 ( )
3. 下列函数中有两个零点的是 ( )
4. 方程的根的个数为 ( )
(A).0 (B).1 (C).2 (D).3
5. 方程的解的个数是 ( )
(A).0 (B).1 (C).2 (D).与a的取值有关
6. 下列函数图象与x轴均有交点,其中不能用二分法求图中交点的横坐标的是( )
y y y y
0 1 2 3 x 0 1 x 0 1 x 0 1 2 x
(A) (B) (C) (D)
7. 函数的零点为 ( )
(A). (B). (C). (D).
8.如果函数在区间(-1,0)内存在零点,则a的取值可以是 ( )
(A) (B)0 (C) (D) –1
填空题:
9.函数在R上的零点有________个.
10.已知函数,若f(x)在R上有一个零点,a=_______;若f(x)在R 上有2个零点,则a的取值范围为______________.
11.方程有两个不等实根,且,则实数k的取值范围为_________.
12.若函数有零点,则实数m的取值范围是___________.
13.已知函数是R上的奇函数,则函数的图象关于_______对称; 若有2005个零点(记为),则_____.
三. 解答题:
14. 已知函数,判断方程在区间[1,1.5]内是否有实数解,如果有,求出一个近似解(精确到0.1).
17. (15分)一种放射性元素,其最初的质量为500g,按每年10%的速度衰减,
(1)求t年后,这种放射性元素的质量m的表达式;
(2)求这种放射性元素的半衰期(精确到0.1年,)
18.(15分)某商店如果将进货为8元的商品按每件10元售出,每天可销售200件,现在采用提高售价,减少进货量的方法增加利润,已知这种商品每涨价0.5元,其销售量就减少10件,问应该将售价定为多少时,才能使所赚利润最大,并求出最大利润.
20.(15分)某市电力公司在电力供大于求时期为了鼓励居民用电,采用分段计费方法计算电费,每月用电不超过100度时,按每度0.57元计费;每月用电超过100度时,其中的100度仍按原标准收费,超过部分按每度0.5元计费.
(1)设每月用电x度,应交电费y元,写出y关于x的函数关系.
(2)小王家第一季度共用了多少度电
月份 1月份 2月份 3月份 合计
缴费金额 76元 63元 45元6角 184元6角
问:小王家第一季度共用了多少度电
参考答案:
一.1-8:A D D B D、A C D
二.9.1; 10.±2, {a|a>2或a<-2}; 11.(0,);
12.(0,1); 13.原点,0
三.14. 1.3;15.(1){x|
