人教版六年级上册第五章5.4复杂图形的面积,确定起跑线同步学案
文档属性
| 名称 | 人教版六年级上册第五章5.4复杂图形的面积,确定起跑线同步学案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 20:42:34 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第四讲 复杂图形的阴影部分面积 确定起跑线
【知识巩固】
一、求一些特殊的图形:
1.弓形:
弓形通常只求面积
弓形面积=扇形面积-三角形面积(除了半圆)
2.“弯角”:
弯角的面积=正方形-扇形
3.“谷子”:
“谷子”的面积=弓形面积×2
求阴影部分的常用方法
1.转化法:就是通过等积变换、平移、旋转、割补等方法将不规则的图形转化成面积额规则图形,再利用规则图形额面积计算公式,计算出所求的不规则图形的面积.
2.和差法:有一些结构复杂,通过观察,分析出不规则图形的面积是由哪些规则图形组合而成的,再利用这些规则图形的面积的和或差来求,从而达到化繁为简的目的.
3.重叠法:就是把所求阴影部分的面积问题转化为可求面积的规则图形的重叠部分的方法,这些阴影一般是由几个图形叠加而成,要准确认清其结构,理顺图形间的大小关系.
4.补形法:将不规则图形补成特殊图形,利用特殊图形的面积求出原不规则图形的面积.
5.拼接法:将不规则的图形进行拼接,利用拼成的特殊图形去计算出原面积.
6.特殊位置法:在大半圆中,任意移动小半圆的位置,阴影部分保留不变,所以可以将小半圆移动到两个半圆同圆心位置.
三、确定起跑线
因为跑道的长度与直道无关,内外跑道的长度不一样,而外圈跑道围成额圆的周长比内圈跑道围成额圆的周长大,只要计算出各圆的周长,再算出相邻两圆额周长相差多少,就得出相邻跑道的距离了.
【典例精讲】
题型1:复杂图形的阴影部分面积
例1.求下图中阴影图形的面积
例2.求下图中阴影图形的面积
例3.已知直角三角形面积是32平方厘米,求阴影部分的面积
例4.图中圆的半径为5厘米,EC长是12厘米 求阴影部分的面积
题型2:确定起跑线
例1.在标准400m跑道上,参加200m跑,每条跑道宽1.25m,相邻跑道中两人之间的跑道位置大约相差多少米?(π取3.14)
例2.一条跑道全长400米,弯道最内圈半径是36米,每条跑道宽1.2米,现有8个弯道.
若进行400米赛跑,第3道运动员的起跑线应比第1道运动员的起跑线提前多少米?
若进行800米赛跑,每名选手必须在自己的跑道上跑完全程,这样,第8道运动员的起跑线应比第一道运动员的起跑线提前多少米?
【课堂练习】
题型1:复杂图形的阴影部分面积
【基础练习】
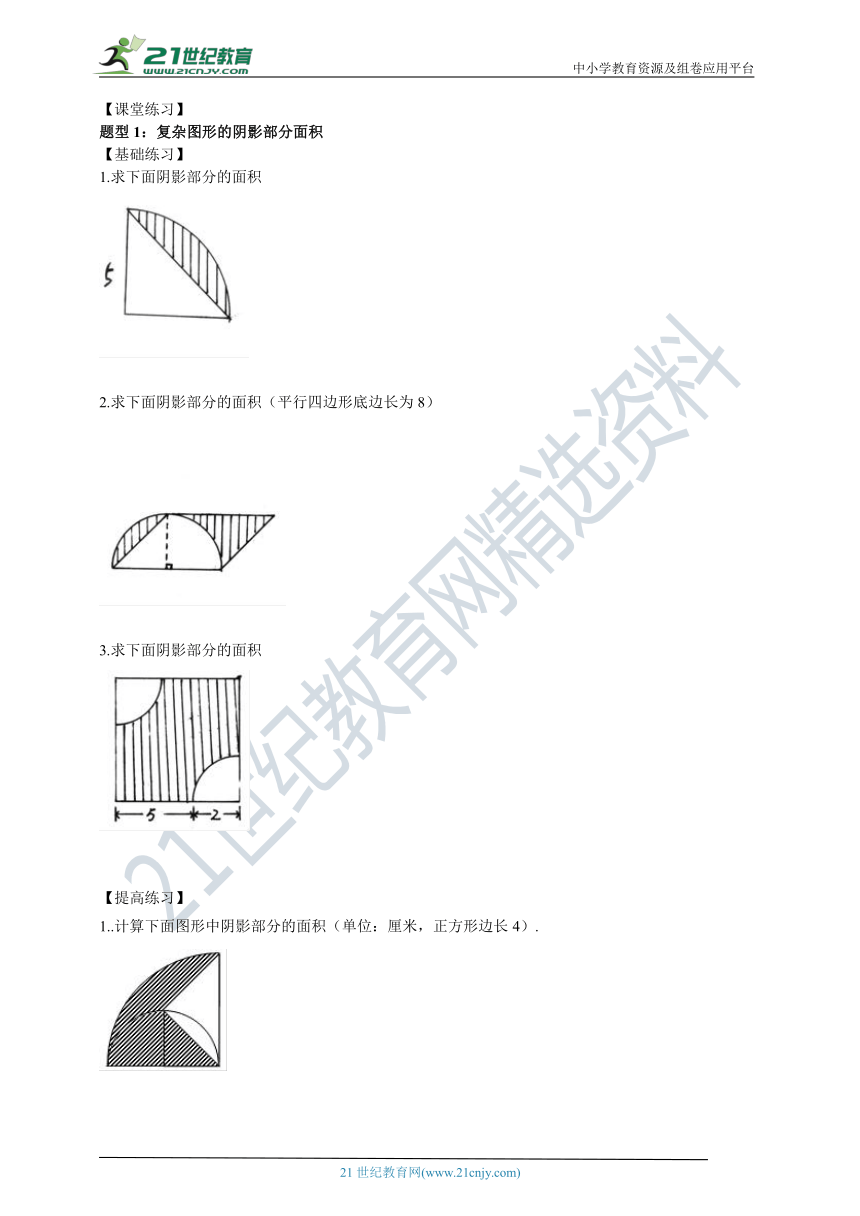
1.求下面阴影部分的面积
2.求下面阴影部分的面积(平行四边形底边长为8)
3.求下面阴影部分的面积
【提高练习】
1..计算下面图形中阴影部分的面积(单位:厘米,正方形边长4).
2..计算下面图形中阴影部分的面积(单位:厘米,正方形边长4).
3.如图,在△ABC中,以AB为直径的圆交BC于D,则图中阴影部分的面积为( ).
(A) (B)2 (C) (D)
4.如图,圆O的直径是8厘米,则阴影部分的面积是多少平方厘米?
5.如图,AD=DB=DC=10厘米,阴影部分的面积是多少平方厘米?
题型2:确定起跑线
【基础练习】
1.半径是5.5米的圆的周长是( ).
2.在圆环中,外圆的直径是13米,内圆的直径是12米,这个圆环的面积是多少?
3.在环形跑道上,第二道与第一道的中间线的距离是0.8米,则第二道的起跑线应比第一道靠前( ).
【提高练习】
1.一条公路有一个半圆形弯道(如图),淘气要从一端走向另一端.
如果淘气沿着弯道的内圈走,淘气沿着弯道的外圈走,两种走法相差多少米
2.在学校的跑道上举行200米赛跑,将跑道划分成1.2米宽的小赛道,第一赛道与第二赛道在弯道处相差多少米 第二赛道的起跑线应比第一赛道的起跑线提前多少米
3.直线的长度是85.96米,第一条半圆形起跑线的直径为72.6米,每条跑道宽1.25米,各跑道的起跑线应该相差多少米呢?
4.每条跑道宽1.25米,第五跑道比第一跑道的起跑线,要前移多少米?
5.在一条标准跑道上,第一条半圆形跑道额半径为36.3米,每条跑道宽1.25宽,200米决赛,第二道比第一道,起跑线前移多少米?
6.有一条200米环形跑道,它是由两个直道的两个半圆形跑道组成,直道长50米,每条跑道宽1.25米,如果在这个跑道上进行100米赛跑,要怎么确定起跑线?
参考答案
【典例精讲】
例1.【解析】:阴影部分面积是三角形面积加半圆面积减去重叠部分面积.
例2.【答案】:20.565平方厘米.
例3.【解析】:(1)求一个谷子面积×4;(2)将左下谷子移动右上补起来刚好是一个三角形;(3)长方形面积减去四分之一圆和弯角面积之和
例4.【解析】:(1)9.12.(2)8.(3)4.355.
【解析】:一个谷子面积加一个弓形面积
例5.【答案】:13.68.
【解析】:将上面两个弓形移到下面去,组合起来阴影部分面积就是梯形减去三角形面积
例6.【答案】:30平方厘米
【解析】:相邻跑道一圈相差7.85m,200减半则为3.925m
例7.【答案】:3.925m
【解析】:跑完全程通过一个全圆,第3弯道比第一弯道半径大2.4米,则需要提前2πr=15.0272米.
例8.【答案】:15.072米.
【解析】:跑完全程通过一个全圆,第8弯道比第一弯道半径大7×1.2=8.4米,需要提前3.14×8.4
×2=52.752米.
例9.【答案】:52.752米.
【巩固练习】
【题型1】
【基础练习】
1.【解析】:
2.【解析】:
3.【解析】:
【提高练习】
1.【解析】:平方厘米.
2.【解析】:平方厘米.
3.【解析】:.
4.【解析】:平方厘米.
5.【解析】:平方厘米.
【题型2】
【基础练习】
1.【解析】:5.5×π×2=34.54米.
2.【解析】:平方分米.
3.【解析】:18.84÷3.14÷2=3米.
【巩固练习】
1.【解析】:9.42米
2.【解析】:9.6米.
3.【解析】:54.95米.
4.【解析】:15.7米.
5.【解析】:7.85米.
6.【解析】:22.93米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第四讲 复杂图形的阴影部分面积 确定起跑线
【知识巩固】
一、求一些特殊的图形:
1.弓形:
弓形通常只求面积
弓形面积=扇形面积-三角形面积(除了半圆)
2.“弯角”:
弯角的面积=正方形-扇形
3.“谷子”:
“谷子”的面积=弓形面积×2
求阴影部分的常用方法
1.转化法:就是通过等积变换、平移、旋转、割补等方法将不规则的图形转化成面积额规则图形,再利用规则图形额面积计算公式,计算出所求的不规则图形的面积.
2.和差法:有一些结构复杂,通过观察,分析出不规则图形的面积是由哪些规则图形组合而成的,再利用这些规则图形的面积的和或差来求,从而达到化繁为简的目的.
3.重叠法:就是把所求阴影部分的面积问题转化为可求面积的规则图形的重叠部分的方法,这些阴影一般是由几个图形叠加而成,要准确认清其结构,理顺图形间的大小关系.
4.补形法:将不规则图形补成特殊图形,利用特殊图形的面积求出原不规则图形的面积.
5.拼接法:将不规则的图形进行拼接,利用拼成的特殊图形去计算出原面积.
6.特殊位置法:在大半圆中,任意移动小半圆的位置,阴影部分保留不变,所以可以将小半圆移动到两个半圆同圆心位置.
三、确定起跑线
因为跑道的长度与直道无关,内外跑道的长度不一样,而外圈跑道围成额圆的周长比内圈跑道围成额圆的周长大,只要计算出各圆的周长,再算出相邻两圆额周长相差多少,就得出相邻跑道的距离了.
【典例精讲】
题型1:复杂图形的阴影部分面积
例1.求下图中阴影图形的面积
例2.求下图中阴影图形的面积
例3.已知直角三角形面积是32平方厘米,求阴影部分的面积
例4.图中圆的半径为5厘米,EC长是12厘米 求阴影部分的面积
题型2:确定起跑线
例1.在标准400m跑道上,参加200m跑,每条跑道宽1.25m,相邻跑道中两人之间的跑道位置大约相差多少米?(π取3.14)
例2.一条跑道全长400米,弯道最内圈半径是36米,每条跑道宽1.2米,现有8个弯道.
若进行400米赛跑,第3道运动员的起跑线应比第1道运动员的起跑线提前多少米?
若进行800米赛跑,每名选手必须在自己的跑道上跑完全程,这样,第8道运动员的起跑线应比第一道运动员的起跑线提前多少米?
【课堂练习】
题型1:复杂图形的阴影部分面积
【基础练习】
1.求下面阴影部分的面积
2.求下面阴影部分的面积(平行四边形底边长为8)
3.求下面阴影部分的面积
【提高练习】
1..计算下面图形中阴影部分的面积(单位:厘米,正方形边长4).
2..计算下面图形中阴影部分的面积(单位:厘米,正方形边长4).
3.如图,在△ABC中,以AB为直径的圆交BC于D,则图中阴影部分的面积为( ).
(A) (B)2 (C) (D)
4.如图,圆O的直径是8厘米,则阴影部分的面积是多少平方厘米?
5.如图,AD=DB=DC=10厘米,阴影部分的面积是多少平方厘米?
题型2:确定起跑线
【基础练习】
1.半径是5.5米的圆的周长是( ).
2.在圆环中,外圆的直径是13米,内圆的直径是12米,这个圆环的面积是多少?
3.在环形跑道上,第二道与第一道的中间线的距离是0.8米,则第二道的起跑线应比第一道靠前( ).
【提高练习】
1.一条公路有一个半圆形弯道(如图),淘气要从一端走向另一端.
如果淘气沿着弯道的内圈走,淘气沿着弯道的外圈走,两种走法相差多少米
2.在学校的跑道上举行200米赛跑,将跑道划分成1.2米宽的小赛道,第一赛道与第二赛道在弯道处相差多少米 第二赛道的起跑线应比第一赛道的起跑线提前多少米
3.直线的长度是85.96米,第一条半圆形起跑线的直径为72.6米,每条跑道宽1.25米,各跑道的起跑线应该相差多少米呢?
4.每条跑道宽1.25米,第五跑道比第一跑道的起跑线,要前移多少米?
5.在一条标准跑道上,第一条半圆形跑道额半径为36.3米,每条跑道宽1.25宽,200米决赛,第二道比第一道,起跑线前移多少米?
6.有一条200米环形跑道,它是由两个直道的两个半圆形跑道组成,直道长50米,每条跑道宽1.25米,如果在这个跑道上进行100米赛跑,要怎么确定起跑线?
参考答案
【典例精讲】
例1.【解析】:阴影部分面积是三角形面积加半圆面积减去重叠部分面积.
例2.【答案】:20.565平方厘米.
例3.【解析】:(1)求一个谷子面积×4;(2)将左下谷子移动右上补起来刚好是一个三角形;(3)长方形面积减去四分之一圆和弯角面积之和
例4.【解析】:(1)9.12.(2)8.(3)4.355.
【解析】:一个谷子面积加一个弓形面积
例5.【答案】:13.68.
【解析】:将上面两个弓形移到下面去,组合起来阴影部分面积就是梯形减去三角形面积
例6.【答案】:30平方厘米
【解析】:相邻跑道一圈相差7.85m,200减半则为3.925m
例7.【答案】:3.925m
【解析】:跑完全程通过一个全圆,第3弯道比第一弯道半径大2.4米,则需要提前2πr=15.0272米.
例8.【答案】:15.072米.
【解析】:跑完全程通过一个全圆,第8弯道比第一弯道半径大7×1.2=8.4米,需要提前3.14×8.4
×2=52.752米.
例9.【答案】:52.752米.
【巩固练习】
【题型1】
【基础练习】
1.【解析】:
2.【解析】:
3.【解析】:
【提高练习】
1.【解析】:平方厘米.
2.【解析】:平方厘米.
3.【解析】:.
4.【解析】:平方厘米.
5.【解析】:平方厘米.
【题型2】
【基础练习】
1.【解析】:5.5×π×2=34.54米.
2.【解析】:平方分米.
3.【解析】:18.84÷3.14÷2=3米.
【巩固练习】
1.【解析】:9.42米
2.【解析】:9.6米.
3.【解析】:54.95米.
4.【解析】:15.7米.
5.【解析】:7.85米.
6.【解析】:22.93米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
