华师大版九年级数学上册第24章解直角三角形检测题(Word版 含答案)
文档属性
| 名称 | 华师大版九年级数学上册第24章解直角三角形检测题(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 485.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 00:00:00 | ||
图片预览



文档简介
第24章检测题
(时间:100分钟 满分:120分)
一、精心选一选(每小题3分,共30分)
1.(大庆中考)2cos
60°=(
)
A.1 B. C. D.
2.河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比为1∶(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是(
)
A.5米
B.10米
C.15米
D.10米
3.(2019·宜昌)如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin
∠BAC的值为(
)
A.
B.
C.
D.
4.在△ABC中,若sin
A=,tan
B=1,则这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
5.式子2cos30°-tan45°-的值是(
)
A.2-2
B.0
C.2
D.2
6.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cos
α=,AB=4,则AC的长为(
)
A.3
B.
C.
D.
7.(2019·益阳)南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为(
)
A.a
sin
α+a
sin
β
B.a
cos
α+a
cos
β
C.a
tan
α+a
tan
β
D.+
8.(2019·营口)如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan
∠BAC的值是(
)
A.
B.
C.
D.
9.(绵阳中考)一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:≈1.732,≈1.414)(
)
A.4.64海里
B.5.49海里
C.6.12海里
D.6.21海里
10.(2019·重庆)如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1∶2.4,那么建筑物AB的高度约为(参考数据sin
27°≈0.45,cos
27°≈0.89,tan
27°≈0.51)(
)
A.65.8米
B.71.8米
C.73.8米
D.119.8米
二、细心填一填(每小题3分,共15分)
11.若α为锐角,cos
α=,则sin
α=(
),tan
α=(
).
12.在Rt△ABC中,∠C=90°,tan
A=,△ABC的周长为18,则S△ABC=(
).
13.在△ABC中,若|2cos
A-1|+(-tan
B)2=0,则∠C=(
).
14.(2019·天门)如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已知CD=9.6
m,则旗杆AB的高度为(
)m.
15.(2019·辽阳)某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车_(
)(填“超速”或“没有超速”).(参考数据:≈1.732)
三、用心做一做(共75分)
16.(8分)解下列各题:
(1)先化简,再求代数式(+)÷的值,其中x=cos30°+;
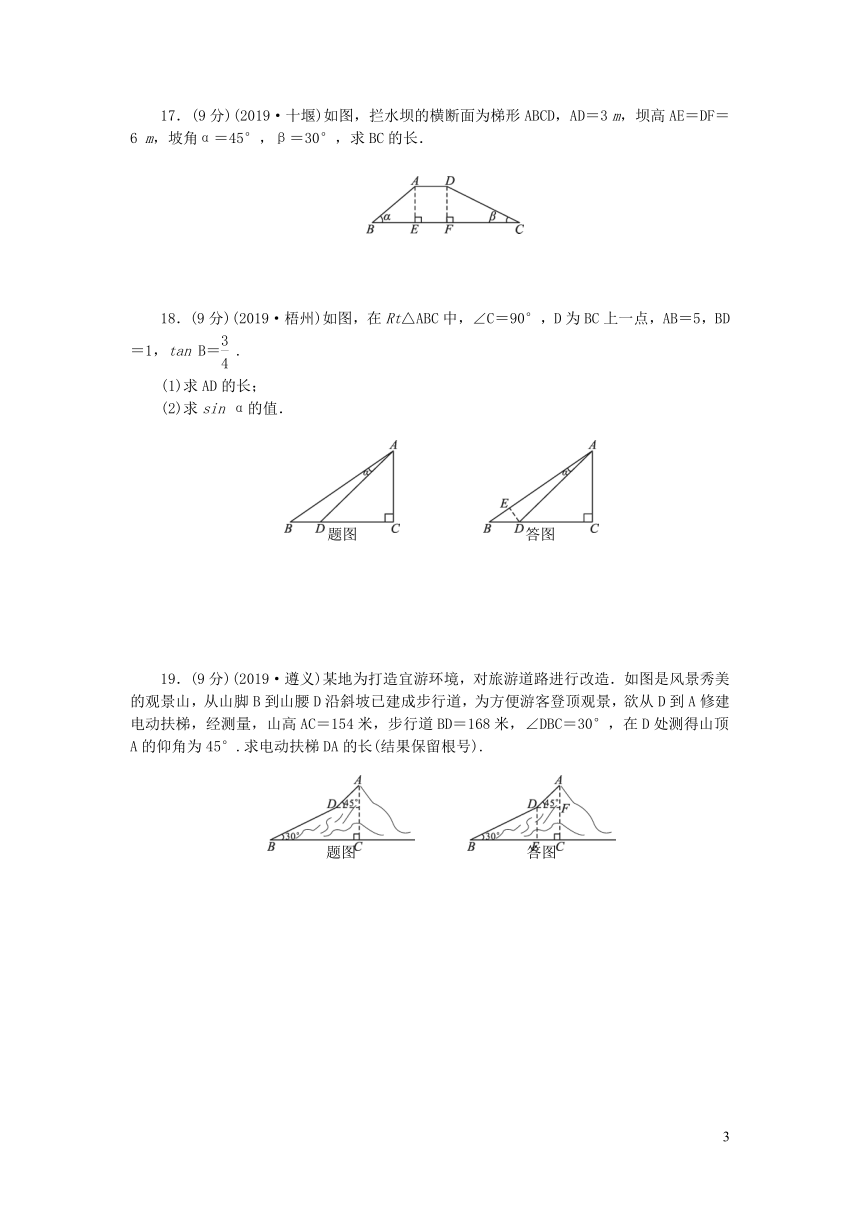
17.(9分)(2019·十堰)如图,拦水坝的横断面为梯形ABCD,AD=3
m,坝高AE=DF=6
m,坡角α=45°,β=30°,求BC的长.
18.(9分)(2019·梧州)如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tan
B=.
(1)求AD的长;
(2)求sin
α的值.
19.(9分)(2019·遵义)某地为打造宜游环境,对旅游道路进行改造.如图是风景秀美的观景山,从山脚B到山腰D沿斜坡已建成步行道,为方便游客登顶观景,欲从D到A修建电动扶梯,经测量,山高AC=154米,步行道BD=168米,∠DBC=30°,在D处测得山顶A的仰角为45°.求电动扶梯DA的长(结果保留根号).
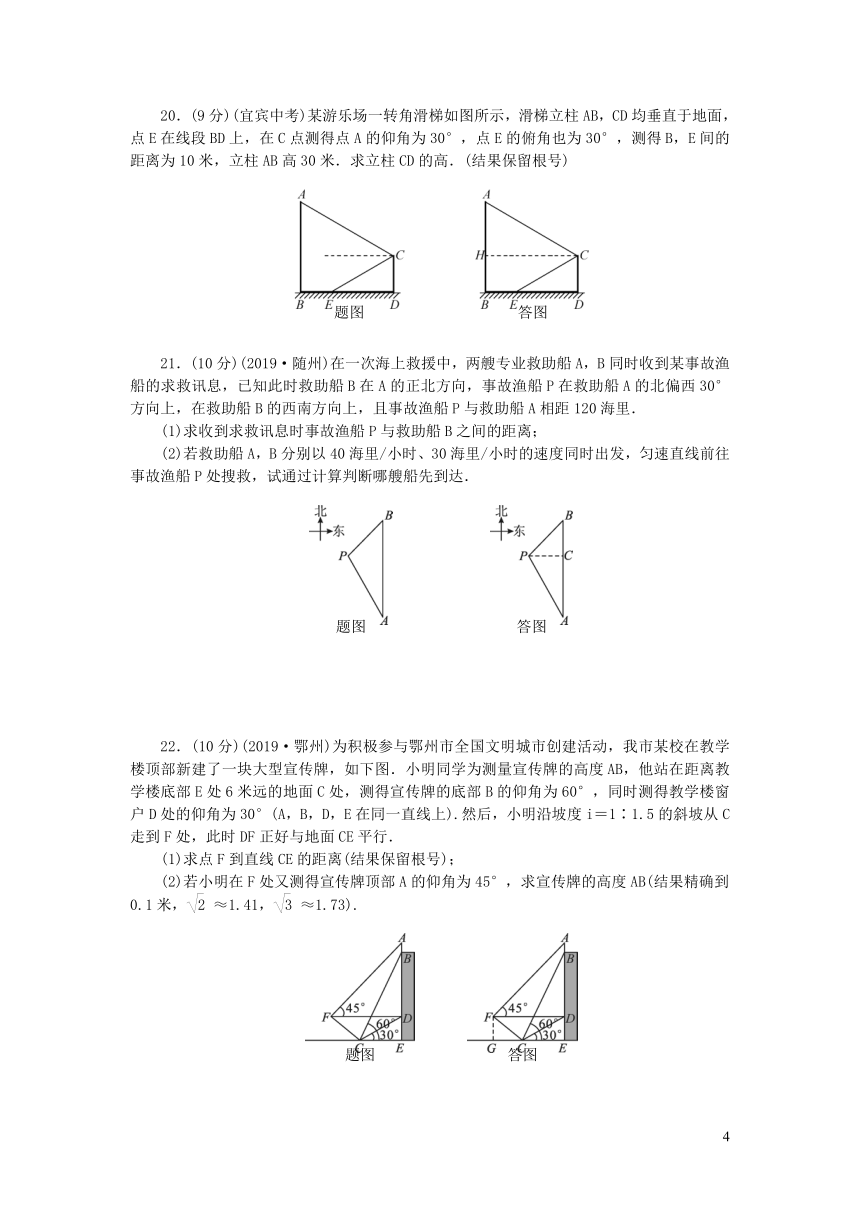
20.(9分)(宜宾中考)某游乐场一转角滑梯如图所示,滑梯立柱AB,CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B,E间的距离为10米,立柱AB高30米.求立柱CD的高.(结果保留根号)
21.(10分)(2019·随州)在一次海上救援中,两艘专业救助船A,B同时收到某事故渔船的求救讯息,已知此时救助船B在A的正北方向,事故渔船P在救助船A的北偏西30°方向上,在救助船B的西南方向上,且事故渔船P与救助船A相距120海里.
(1)求收到求救讯息时事故渔船P与救助船B之间的距离;
(2)若救助船A,B分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船P处搜救,试通过计算判断哪艘船先到达.
22.(10分)(2019·鄂州)为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A,B,D,E在同一直线上).然后,小明沿坡度i=1∶1.5的斜坡从C走到F处,此时DF正好与地面CE平行.
(1)求点F到直线CE的距离(结果保留根号);
(2)若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米,≈1.41,≈1.73).
23.(11分)(赤峰中考)阅读下列材料:
如图①,在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,可以得到:S△ABC=ab
sin
C=ac
sin
B=bc
sin
A.证明:过点A作AD⊥BC,垂足为D.在Rt△ABD中,sin
B=,∴AD=c·sin
B,∴S△ABC=a·AD=ac
sin
B,同理:S△ABC=ab
sin
C,S△ABC=bc
sin
A,∴S△ABC=ab
sin
C=ac
sin
B=bc
sin
A.
(1)通过上述材料证明:==;
(2)运用(1)中的结论解决问题:如图②,在△ABC中,∠B=15°,∠C=60°,AB=20,求AC的长度;
(3)如图③,为了开发公路旁的城市荒地,测量人员选择A,B,C三个测量点,在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18
km到达C点,测得A在北偏西45°方向上,根据以上信息,求A,B,C三点围成的三角形的面积.(本题参考数值:sin
15°≈0.3,sin
120°≈0.9,≈1.4,结果取整数)
第24章检测题(答案版)
(时间:100分钟 满分:120分)
一、精心选一选(每小题3分,共30分)
1.(大庆中考)2cos
60°=(
A
)
A.1 B. C. D.
2.河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比为1∶(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是(
A
)
A.5米
B.10米
C.15米
D.10米
3.(2019·宜昌)如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin
∠BAC的值为(
D
)
A.
B.
C.
D.
4.在△ABC中,若sin
A=,tan
B=1,则这个三角形是(
A
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
5.式子2cos30°-tan45°-的值是(
B
)
A.2-2
B.0
C.2
D.2
6.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cos
α=,AB=4,则AC的长为(
C
)
A.3
B.
C.
D.
7.(2019·益阳)南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为(
C
)
A.a
sin
α+a
sin
β
B.a
cos
α+a
cos
β
C.a
tan
α+a
tan
β
D.+
8.(2019·营口)如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan
∠BAC的值是(
C
)
A.
B.
C.
D.
9.(绵阳中考)一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:≈1.732,≈1.414)(
B
)
A.4.64海里
B.5.49海里
C.6.12海里
D.6.21海里
10.(2019·重庆)如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1∶2.4,那么建筑物AB的高度约为(参考数据sin
27°≈0.45,cos
27°≈0.89,tan
27°≈0.51)(
B
)
A.65.8米
B.71.8米
C.73.8米
D.119.8米
二、细心填一填(每小题3分,共15分)
11.若α为锐角,cos
α=,则sin
α=____,tan
α=____.
12.在Rt△ABC中,∠C=90°,tan
A=,△ABC的周长为18,则S△ABC=____.
13.在△ABC中,若|2cos
A-1|+(-tan
B)2=0,则∠C=__60°__.
14.(2019·天门)如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已知CD=9.6
m,则旗杆AB的高度为__14.4__m.
15.(2019·辽阳)某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车__没有超速__(填“超速”或“没有超速”).(参考数据:≈1.732)
三、用心做一做(共75分)
16.(8分)解下列各题:
(1)先化简,再求代数式(+)÷的值,其中x=cos30°+;
解:x=2,原式=x+1=3
(2)已知α是锐角,且sin
(α+15°)=.计算-4cos
α-(π-3.14)0+tan
α+()-1的值.
解:α=45°,原式=3
17.(9分)(2019·十堰)如图,拦水坝的横断面为梯形ABCD,AD=3
m,坝高AE=DF=6
m,坡角α=45°,β=30°,求BC的长.
解:由图得,AE,DF为高,则四边形AEFD是矩形,有AE=DF=6,AD=EF=3,∵坡角α=45°,β=30°,∴BE=AE=6,CF=DF=6,∴BC=BE+EF+CF=6+3+6=9+6,答:BC的长(9+6)m
18.(9分)(2019·梧州)如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tan
B=.
(1)求AD的长;
(2)求sin
α的值.
解:(1)∵tan
B=,可设AC=3x,得BC=4x,∵AC2+BC2=AB2,∴(3x)2+(4x)2=52,解得x=-1(舍去)或x=1,∴AC=3,BC=4,∵BD=1,∴CD=3,∴AD==3
(2)如图,过点D作DE⊥AB于点E,∵tan
B=,可设DE=3y,则BE=4y,∵BE2+DE2=BD2,∴(4y)2+(3y)2=12,解得y=-(舍)或y=,∴DE=,∴sin
α==
19.(9分)(2019·遵义)某地为打造宜游环境,对旅游道路进行改造.如图是风景秀美的观景山,从山脚B到山腰D沿斜坡已建成步行道,为方便游客登顶观景,欲从D到A修建电动扶梯,经测量,山高AC=154米,步行道BD=168米,∠DBC=30°,在D处测得山顶A的仰角为45°.求电动扶梯DA的长(结果保留根号).
解:作DE⊥BC于E,则四边形DECF为矩形,∴FC=DE,DF=EC,在Rt△DBE中,∠DBC=30°,∴DE=BD=84,∴FC=DE=84,∴AF=AC-FC=154-84=70,在Rt△ADF中,∠ADF=45°,∴AD=AF=70,答:电动扶梯DA的长为70米
20.(9分)(宜宾中考)某游乐场一转角滑梯如图所示,滑梯立柱AB,CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B,E间的距离为10米,立柱AB高30米.求立柱CD的高.(结果保留根号)
解:如图,作CH⊥AB于H,则四边形HBDC为矩形,∴BD=CH,由题意得,∠ACH=30°,∠CED=30°,设CD=x米,则AH=(30-x)米,在Rt△AHC中,HC==(30-x),则BD=CH=(30-x),∴ED=(30-x)-10,在Rt△CDE中,=tan
∠CED,即=,解得x=15-,答:立柱CD的高为(15-)米
21.(10分)(2019·随州)在一次海上救援中,两艘专业救助船A,B同时收到某事故渔船的求救讯息,已知此时救助船B在A的正北方向,事故渔船P在救助船A的北偏西30°方向上,在救助船B的西南方向上,且事故渔船P与救助船A相距120海里.
(1)求收到求救讯息时事故渔船P与救助船B之间的距离;
(2)若救助船A,B分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船P处搜救,试通过计算判断哪艘船先到达.
解:(1)如图所示:作PC⊥AB于C,则∠PCA=∠PCB=90°,由题意得PA=120海里,∠A=30°,∠BPC=45°,∴PC=PA=60海里,△BCP是等腰直角三角形,∴BC=PC=60海里,PB=PC=60海里,答:收到求救讯息时事故渔船P与救助船B之间的距离为60海里
(2)∵PA=120海里,PB=60海里,救助船A,B分别以40海里/小时、30海里/小时的速度同时出发,∴救助船A所用的时间为=3(小时),救助船B所用的时间为=2(小时),∵3>2,∴救助船B先到达
22.(10分)(2019·鄂州)为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A,B,D,E在同一直线上).然后,小明沿坡度i=1∶1.5的斜坡从C走到F处,此时DF正好与地面CE平行.
(1)求点F到直线CE的距离(结果保留根号);
(2)若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米,≈1.41,≈1.73).
解:(1)过点F作FG⊥EC于G,依题意知FG∥DE,DF∥GE,∠FGE=90°,∴四边形DEGF是矩形,∴FG=DE,在Rt△CDE中,DE=CE·tan
∠DCE=6×tan
30°=2(米),∴点F到地面的距离为2
米 (2)∵斜坡CF的坡度为i=1∶1.5,∴在Rt△CFG中,CG=1.5FG=2×1.5=3,∴FD=EG=3+6.在Rt△BCE中,BE=CE·tan
∠BCE=6×tan
60°=6.∴AB=AD+DE-BE=3+6+2-6=6-≈4.3
(米),答:宣传牌的高度约为4.3米
23.(11分)(赤峰中考)阅读下列材料:
如图①,在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,可以得到:S△ABC=ab
sin
C=ac
sin
B=bc
sin
A.证明:过点A作AD⊥BC,垂足为D.在Rt△ABD中,sin
B=,∴AD=c·sin
B,∴S△ABC=a·AD=ac
sin
B,同理:S△ABC=ab
sin
C,S△ABC=bc
sin
A,∴S△ABC=ab
sin
C=ac
sin
B=bc
sin
A.
(1)通过上述材料证明:==;
(2)运用(1)中的结论解决问题:如图②,在△ABC中,∠B=15°,∠C=60°,AB=20,求AC的长度;
(3)如图③,为了开发公路旁的城市荒地,测量人员选择A,B,C三个测量点,在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18
km到达C点,测得A在北偏西45°方向上,根据以上信息,求A,B,C三点围成的三角形的面积.(本题参考数值:sin
15°≈0.3,sin
120°≈0.9,≈1.4,结果取整数)
解:(1)∵ab
sin
C=ac
sin
B,∴b
sin
C=c
sin
B,∴=,同理得,=,∴== (2)由题意,得∠B=15°,∠C=60°,AB=20,∴=,即=,∴=,∴AC=40×0.3=12 (3)由题意,得∠ABC=90°-75°=15°,∠ACB=90°-45°=45°,∠A=180°-15°-45°=120°,由==,得=,∴AC=6
km,∴S△ABC=AC×BC×sin
∠ACB=×6×18×0.7≈38(km2)
6
(时间:100分钟 满分:120分)
一、精心选一选(每小题3分,共30分)
1.(大庆中考)2cos
60°=(
)
A.1 B. C. D.
2.河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比为1∶(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是(
)
A.5米
B.10米
C.15米
D.10米
3.(2019·宜昌)如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin
∠BAC的值为(
)
A.
B.
C.
D.
4.在△ABC中,若sin
A=,tan
B=1,则这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
5.式子2cos30°-tan45°-的值是(
)
A.2-2
B.0
C.2
D.2
6.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cos
α=,AB=4,则AC的长为(
)
A.3
B.
C.
D.
7.(2019·益阳)南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为(
)
A.a
sin
α+a
sin
β
B.a
cos
α+a
cos
β
C.a
tan
α+a
tan
β
D.+
8.(2019·营口)如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan
∠BAC的值是(
)
A.
B.
C.
D.
9.(绵阳中考)一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:≈1.732,≈1.414)(
)
A.4.64海里
B.5.49海里
C.6.12海里
D.6.21海里
10.(2019·重庆)如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1∶2.4,那么建筑物AB的高度约为(参考数据sin
27°≈0.45,cos
27°≈0.89,tan
27°≈0.51)(
)
A.65.8米
B.71.8米
C.73.8米
D.119.8米
二、细心填一填(每小题3分,共15分)
11.若α为锐角,cos
α=,则sin
α=(
),tan
α=(
).
12.在Rt△ABC中,∠C=90°,tan
A=,△ABC的周长为18,则S△ABC=(
).
13.在△ABC中,若|2cos
A-1|+(-tan
B)2=0,则∠C=(
).
14.(2019·天门)如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已知CD=9.6
m,则旗杆AB的高度为(
)m.
15.(2019·辽阳)某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车_(
)(填“超速”或“没有超速”).(参考数据:≈1.732)
三、用心做一做(共75分)
16.(8分)解下列各题:
(1)先化简,再求代数式(+)÷的值,其中x=cos30°+;
17.(9分)(2019·十堰)如图,拦水坝的横断面为梯形ABCD,AD=3
m,坝高AE=DF=6
m,坡角α=45°,β=30°,求BC的长.
18.(9分)(2019·梧州)如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tan
B=.
(1)求AD的长;
(2)求sin
α的值.
19.(9分)(2019·遵义)某地为打造宜游环境,对旅游道路进行改造.如图是风景秀美的观景山,从山脚B到山腰D沿斜坡已建成步行道,为方便游客登顶观景,欲从D到A修建电动扶梯,经测量,山高AC=154米,步行道BD=168米,∠DBC=30°,在D处测得山顶A的仰角为45°.求电动扶梯DA的长(结果保留根号).
20.(9分)(宜宾中考)某游乐场一转角滑梯如图所示,滑梯立柱AB,CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B,E间的距离为10米,立柱AB高30米.求立柱CD的高.(结果保留根号)
21.(10分)(2019·随州)在一次海上救援中,两艘专业救助船A,B同时收到某事故渔船的求救讯息,已知此时救助船B在A的正北方向,事故渔船P在救助船A的北偏西30°方向上,在救助船B的西南方向上,且事故渔船P与救助船A相距120海里.
(1)求收到求救讯息时事故渔船P与救助船B之间的距离;
(2)若救助船A,B分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船P处搜救,试通过计算判断哪艘船先到达.
22.(10分)(2019·鄂州)为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A,B,D,E在同一直线上).然后,小明沿坡度i=1∶1.5的斜坡从C走到F处,此时DF正好与地面CE平行.
(1)求点F到直线CE的距离(结果保留根号);
(2)若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米,≈1.41,≈1.73).
23.(11分)(赤峰中考)阅读下列材料:
如图①,在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,可以得到:S△ABC=ab
sin
C=ac
sin
B=bc
sin
A.证明:过点A作AD⊥BC,垂足为D.在Rt△ABD中,sin
B=,∴AD=c·sin
B,∴S△ABC=a·AD=ac
sin
B,同理:S△ABC=ab
sin
C,S△ABC=bc
sin
A,∴S△ABC=ab
sin
C=ac
sin
B=bc
sin
A.
(1)通过上述材料证明:==;
(2)运用(1)中的结论解决问题:如图②,在△ABC中,∠B=15°,∠C=60°,AB=20,求AC的长度;
(3)如图③,为了开发公路旁的城市荒地,测量人员选择A,B,C三个测量点,在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18
km到达C点,测得A在北偏西45°方向上,根据以上信息,求A,B,C三点围成的三角形的面积.(本题参考数值:sin
15°≈0.3,sin
120°≈0.9,≈1.4,结果取整数)
第24章检测题(答案版)
(时间:100分钟 满分:120分)
一、精心选一选(每小题3分,共30分)
1.(大庆中考)2cos
60°=(
A
)
A.1 B. C. D.
2.河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比为1∶(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是(
A
)
A.5米
B.10米
C.15米
D.10米
3.(2019·宜昌)如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin
∠BAC的值为(
D
)
A.
B.
C.
D.
4.在△ABC中,若sin
A=,tan
B=1,则这个三角形是(
A
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
5.式子2cos30°-tan45°-的值是(
B
)
A.2-2
B.0
C.2
D.2
6.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cos
α=,AB=4,则AC的长为(
C
)
A.3
B.
C.
D.
7.(2019·益阳)南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为(
C
)
A.a
sin
α+a
sin
β
B.a
cos
α+a
cos
β
C.a
tan
α+a
tan
β
D.+
8.(2019·营口)如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan
∠BAC的值是(
C
)
A.
B.
C.
D.
9.(绵阳中考)一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:≈1.732,≈1.414)(
B
)
A.4.64海里
B.5.49海里
C.6.12海里
D.6.21海里
10.(2019·重庆)如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1∶2.4,那么建筑物AB的高度约为(参考数据sin
27°≈0.45,cos
27°≈0.89,tan
27°≈0.51)(
B
)
A.65.8米
B.71.8米
C.73.8米
D.119.8米
二、细心填一填(每小题3分,共15分)
11.若α为锐角,cos
α=,则sin
α=____,tan
α=____.
12.在Rt△ABC中,∠C=90°,tan
A=,△ABC的周长为18,则S△ABC=____.
13.在△ABC中,若|2cos
A-1|+(-tan
B)2=0,则∠C=__60°__.
14.(2019·天门)如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已知CD=9.6
m,则旗杆AB的高度为__14.4__m.
15.(2019·辽阳)某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车__没有超速__(填“超速”或“没有超速”).(参考数据:≈1.732)
三、用心做一做(共75分)
16.(8分)解下列各题:
(1)先化简,再求代数式(+)÷的值,其中x=cos30°+;
解:x=2,原式=x+1=3
(2)已知α是锐角,且sin
(α+15°)=.计算-4cos
α-(π-3.14)0+tan
α+()-1的值.
解:α=45°,原式=3
17.(9分)(2019·十堰)如图,拦水坝的横断面为梯形ABCD,AD=3
m,坝高AE=DF=6
m,坡角α=45°,β=30°,求BC的长.
解:由图得,AE,DF为高,则四边形AEFD是矩形,有AE=DF=6,AD=EF=3,∵坡角α=45°,β=30°,∴BE=AE=6,CF=DF=6,∴BC=BE+EF+CF=6+3+6=9+6,答:BC的长(9+6)m
18.(9分)(2019·梧州)如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tan
B=.
(1)求AD的长;
(2)求sin
α的值.
解:(1)∵tan
B=,可设AC=3x,得BC=4x,∵AC2+BC2=AB2,∴(3x)2+(4x)2=52,解得x=-1(舍去)或x=1,∴AC=3,BC=4,∵BD=1,∴CD=3,∴AD==3
(2)如图,过点D作DE⊥AB于点E,∵tan
B=,可设DE=3y,则BE=4y,∵BE2+DE2=BD2,∴(4y)2+(3y)2=12,解得y=-(舍)或y=,∴DE=,∴sin
α==
19.(9分)(2019·遵义)某地为打造宜游环境,对旅游道路进行改造.如图是风景秀美的观景山,从山脚B到山腰D沿斜坡已建成步行道,为方便游客登顶观景,欲从D到A修建电动扶梯,经测量,山高AC=154米,步行道BD=168米,∠DBC=30°,在D处测得山顶A的仰角为45°.求电动扶梯DA的长(结果保留根号).
解:作DE⊥BC于E,则四边形DECF为矩形,∴FC=DE,DF=EC,在Rt△DBE中,∠DBC=30°,∴DE=BD=84,∴FC=DE=84,∴AF=AC-FC=154-84=70,在Rt△ADF中,∠ADF=45°,∴AD=AF=70,答:电动扶梯DA的长为70米
20.(9分)(宜宾中考)某游乐场一转角滑梯如图所示,滑梯立柱AB,CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B,E间的距离为10米,立柱AB高30米.求立柱CD的高.(结果保留根号)
解:如图,作CH⊥AB于H,则四边形HBDC为矩形,∴BD=CH,由题意得,∠ACH=30°,∠CED=30°,设CD=x米,则AH=(30-x)米,在Rt△AHC中,HC==(30-x),则BD=CH=(30-x),∴ED=(30-x)-10,在Rt△CDE中,=tan
∠CED,即=,解得x=15-,答:立柱CD的高为(15-)米
21.(10分)(2019·随州)在一次海上救援中,两艘专业救助船A,B同时收到某事故渔船的求救讯息,已知此时救助船B在A的正北方向,事故渔船P在救助船A的北偏西30°方向上,在救助船B的西南方向上,且事故渔船P与救助船A相距120海里.
(1)求收到求救讯息时事故渔船P与救助船B之间的距离;
(2)若救助船A,B分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船P处搜救,试通过计算判断哪艘船先到达.
解:(1)如图所示:作PC⊥AB于C,则∠PCA=∠PCB=90°,由题意得PA=120海里,∠A=30°,∠BPC=45°,∴PC=PA=60海里,△BCP是等腰直角三角形,∴BC=PC=60海里,PB=PC=60海里,答:收到求救讯息时事故渔船P与救助船B之间的距离为60海里
(2)∵PA=120海里,PB=60海里,救助船A,B分别以40海里/小时、30海里/小时的速度同时出发,∴救助船A所用的时间为=3(小时),救助船B所用的时间为=2(小时),∵3>2,∴救助船B先到达
22.(10分)(2019·鄂州)为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A,B,D,E在同一直线上).然后,小明沿坡度i=1∶1.5的斜坡从C走到F处,此时DF正好与地面CE平行.
(1)求点F到直线CE的距离(结果保留根号);
(2)若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米,≈1.41,≈1.73).
解:(1)过点F作FG⊥EC于G,依题意知FG∥DE,DF∥GE,∠FGE=90°,∴四边形DEGF是矩形,∴FG=DE,在Rt△CDE中,DE=CE·tan
∠DCE=6×tan
30°=2(米),∴点F到地面的距离为2
米 (2)∵斜坡CF的坡度为i=1∶1.5,∴在Rt△CFG中,CG=1.5FG=2×1.5=3,∴FD=EG=3+6.在Rt△BCE中,BE=CE·tan
∠BCE=6×tan
60°=6.∴AB=AD+DE-BE=3+6+2-6=6-≈4.3
(米),答:宣传牌的高度约为4.3米
23.(11分)(赤峰中考)阅读下列材料:
如图①,在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,可以得到:S△ABC=ab
sin
C=ac
sin
B=bc
sin
A.证明:过点A作AD⊥BC,垂足为D.在Rt△ABD中,sin
B=,∴AD=c·sin
B,∴S△ABC=a·AD=ac
sin
B,同理:S△ABC=ab
sin
C,S△ABC=bc
sin
A,∴S△ABC=ab
sin
C=ac
sin
B=bc
sin
A.
(1)通过上述材料证明:==;
(2)运用(1)中的结论解决问题:如图②,在△ABC中,∠B=15°,∠C=60°,AB=20,求AC的长度;
(3)如图③,为了开发公路旁的城市荒地,测量人员选择A,B,C三个测量点,在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18
km到达C点,测得A在北偏西45°方向上,根据以上信息,求A,B,C三点围成的三角形的面积.(本题参考数值:sin
15°≈0.3,sin
120°≈0.9,≈1.4,结果取整数)
解:(1)∵ab
sin
C=ac
sin
B,∴b
sin
C=c
sin
B,∴=,同理得,=,∴== (2)由题意,得∠B=15°,∠C=60°,AB=20,∴=,即=,∴=,∴AC=40×0.3=12 (3)由题意,得∠ABC=90°-75°=15°,∠ACB=90°-45°=45°,∠A=180°-15°-45°=120°,由==,得=,∴AC=6
km,∴S△ABC=AC×BC×sin
∠ACB=×6×18×0.7≈38(km2)
6
