23.2.1中心对称-人教版九年级数学上册练习(Word版 含解析)
文档属性
| 名称 | 23.2.1中心对称-人教版九年级数学上册练习(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 164.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 00:00:00 | ||
图片预览

文档简介
人教版九年级数学上册23.2.1中心对称
一.选择题(共6小题)
1.如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
2.下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组
B.2组
C.3组
D.4组
3.如图,△ABC与△A′B′C′成中心对称,ED是△ABC的中位线,E′D′是△A′B′C′的中位线,已知BC=4,则E′D′=( )
A.2
B.3
C.4
D.1.5
4.如图,已知图形是中心对称图形,则对称中心是( )
A.点C
B.点D
C.线段BC的中点
D.线段FC的中点
5.已知下列命题,其中正确的个数是( )
(1)关于中心对称的两个图形一定不全等;
(2)关于中心对称的两个图形是全等形;
(3)两个全等的图形一定关于中心对称.
A.0个
B.1个
C.2个
D.3个
6.已知△ABC和△DEF关于点O对称,相应的对称点如图所示,则下列结论正确的是( )
A.AO=BO
B.BO=EO
C.点A关于点O的对称点是点D
D.点D
在BO的延长线上
二.填空题(共6小题)
7.关于某一点成中心对称的两个图形,对称点的连线都经过
,并且被
平分.
8.如图,是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为
.
9.如图,△ABC与△DEC关于点C成中心对称,则线段AB与DE的大小关系是
.
10.如图,△ABC绕点A旋转180°,得到△A′B′C′,A为旋转中心,则△ABC与△A′B′C′关于点
中心对称;若∠C=90°,∠B=30°,BC=1,则BB′的长为
.
11.与电子显示的四位数6925不相等,但为全等图形的四位数是
.
12.如图,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.在这种变换下,如果△ABC中任意一点M的坐标为(x,y),那么它们的对应点N的坐标是
.
三.解答题(共3小题)
13.如图所示的两个图形成中心对称,请找出它的对称中点.
14.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
15.如图,矩形ABCD和矩形A'B'C'D关于点D成中心对称.
求证:四边形ACA'C'是菱形.
人教版九年级数学上册23.2.1中心对称参考答案
一.选择题(共6小题)
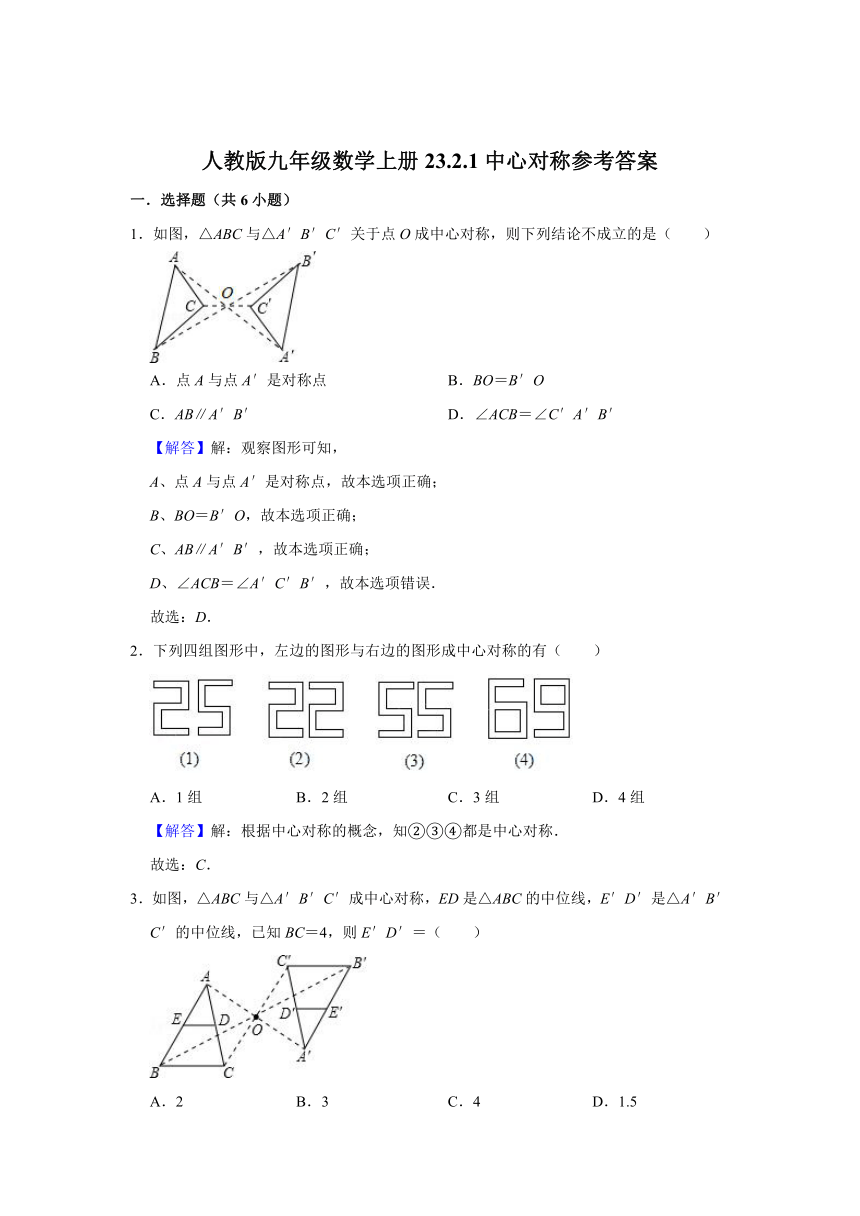
1.如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
【解答】解:观察图形可知,
A、点A与点A′是对称点,故本选项正确;
B、BO=B′O,故本选项正确;
C、AB∥A′B′,故本选项正确;
D、∠ACB=∠A′C′B′,故本选项错误.
故选:D.
2.下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组
B.2组
C.3组
D.4组
【解答】解:根据中心对称的概念,知②③④都是中心对称.
故选:C.
3.如图,△ABC与△A′B′C′成中心对称,ED是△ABC的中位线,E′D′是△A′B′C′的中位线,已知BC=4,则E′D′=( )
A.2
B.3
C.4
D.1.5
【解答】解:∵△ABC与△A′B′C′成中心对称,
∴△ABC≌△A′B′C′,
∴B′C′=BC=4,
∵E′D′是△A′B′C′的中位线,
∴E′D′=B′C′=×4=2.
故选:A.
4.如图,已知图形是中心对称图形,则对称中心是( )
A.点C
B.点D
C.线段BC的中点
D.线段FC的中点
【解答】解:∵此图形是中心对称图形,
∴对称中心是线段FC的中点.
故选:D.
5.已知下列命题,其中正确的个数是( )
(1)关于中心对称的两个图形一定不全等;
(2)关于中心对称的两个图形是全等形;
(3)两个全等的图形一定关于中心对称.
A.0个
B.1个
C.2个
D.3个
【解答】解:关于中心对称的两个图形一定全等,两个全等的图形不一定关于中心对称.
故只有(2)说法正确,
故选:B.
6.已知△ABC和△DEF关于点O对称,相应的对称点如图所示,则下列结论正确的是( )
A.AO=BO
B.BO=EO
C.点A关于点O的对称点是点D
D.点D
在BO的延长线上
【解答】解:A、AO=OE,错误;
B、BO=DO,错误;
C、点A关于点O的对称点是点E,错误;
D、点D
在BO的延长线上,正确;
故选:D.
二.填空题(共6小题)
7.关于某一点成中心对称的两个图形,对称点的连线都经过 对称中心 ,并且被 对称中心 平分.
【解答】解:根据中心对称的性质,得
对称点的连线都经过对称中心,并且被对称中心平分.
8.如图,是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为 4 .
【解答】解:∵在Rt△ABC中,∠B=30°,AC=1,
∴AB=2AC=2,
根据中心对称的性质得到BB′=2AB=4.
故答案为:4.
9.如图,△ABC与△DEC关于点C成中心对称,则线段AB与DE的大小关系是 AB=DE .
【解答】解:∵△ABC与△DEC关于点C成中心对称,
∴AB=DE
故答案为:AB=DE.
10.如图,△ABC绕点A旋转180°,得到△A′B′C′,A为旋转中心,则△ABC与△A′B′C′关于点 A 中心对称;若∠C=90°,∠B=30°,BC=1,则BB′的长为 .
【解答】解:∵如图,△ABC绕点A旋转180°,得到△A′B′C′,A为旋转中心,
∴△ABC与△A′B′C′关于点
A中心对称;
∵在直角△ABC中,∠B=30°,BC=1,
∴AB===
∴BB′=2AB=.
故答案是:A;.
11.与电子显示的四位数6925不相等,但为全等图形的四位数是 5269 .
【解答】答:5269.
12.如图,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.在这种变换下,如果△ABC中任意一点M的坐标为(x,y),那么它们的对应点N的坐标是 (﹣x,﹣y) .
【解答】解:由图可知两三角形关于点O成中心对称,
关于原点成中心对称的坐标的特点为横纵坐标均互为相反数,
故点N的坐标是(﹣x,﹣y).
三.解答题(共3小题)
13.如图所示的两个图形成中心对称,请找出它的对称中点.
【解答】解:连接CC′,BB′,两条线段相交于当O,
则点O即为对称中点.
14.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
【解答】解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8;
(3)∵在△ABD和△CDE中,,
∴△ABD≌△CDE(SAS),
∴AB=CE,AD=DE
∵△ACE中,AC﹣AB<AE<AC+AB,
∴2<AE<8,
∴1<AD<4.
15.如图,矩形ABCD和矩形A'B'C'D关于点D成中心对称.
求证:四边形ACA'C'是菱形.
【解答】解:∵矩形ABCD与矩形AB′C′D′关于点D成中心对称,
∴∠ADC=90°,CD=CD′,DA=DA′,
∴四边形ACA'C'是平行四边形,AA′⊥CC′,
∴四边形ACA'C'是菱形.
一.选择题(共6小题)
1.如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
2.下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组
B.2组
C.3组
D.4组
3.如图,△ABC与△A′B′C′成中心对称,ED是△ABC的中位线,E′D′是△A′B′C′的中位线,已知BC=4,则E′D′=( )
A.2
B.3
C.4
D.1.5
4.如图,已知图形是中心对称图形,则对称中心是( )
A.点C
B.点D
C.线段BC的中点
D.线段FC的中点
5.已知下列命题,其中正确的个数是( )
(1)关于中心对称的两个图形一定不全等;
(2)关于中心对称的两个图形是全等形;
(3)两个全等的图形一定关于中心对称.
A.0个
B.1个
C.2个
D.3个
6.已知△ABC和△DEF关于点O对称,相应的对称点如图所示,则下列结论正确的是( )
A.AO=BO
B.BO=EO
C.点A关于点O的对称点是点D
D.点D
在BO的延长线上
二.填空题(共6小题)
7.关于某一点成中心对称的两个图形,对称点的连线都经过
,并且被
平分.
8.如图,是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为
.
9.如图,△ABC与△DEC关于点C成中心对称,则线段AB与DE的大小关系是
.
10.如图,△ABC绕点A旋转180°,得到△A′B′C′,A为旋转中心,则△ABC与△A′B′C′关于点
中心对称;若∠C=90°,∠B=30°,BC=1,则BB′的长为
.
11.与电子显示的四位数6925不相等,但为全等图形的四位数是
.
12.如图,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.在这种变换下,如果△ABC中任意一点M的坐标为(x,y),那么它们的对应点N的坐标是
.
三.解答题(共3小题)
13.如图所示的两个图形成中心对称,请找出它的对称中点.
14.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
15.如图,矩形ABCD和矩形A'B'C'D关于点D成中心对称.
求证:四边形ACA'C'是菱形.
人教版九年级数学上册23.2.1中心对称参考答案
一.选择题(共6小题)
1.如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
【解答】解:观察图形可知,
A、点A与点A′是对称点,故本选项正确;
B、BO=B′O,故本选项正确;
C、AB∥A′B′,故本选项正确;
D、∠ACB=∠A′C′B′,故本选项错误.
故选:D.
2.下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组
B.2组
C.3组
D.4组
【解答】解:根据中心对称的概念,知②③④都是中心对称.
故选:C.
3.如图,△ABC与△A′B′C′成中心对称,ED是△ABC的中位线,E′D′是△A′B′C′的中位线,已知BC=4,则E′D′=( )
A.2
B.3
C.4
D.1.5
【解答】解:∵△ABC与△A′B′C′成中心对称,
∴△ABC≌△A′B′C′,
∴B′C′=BC=4,
∵E′D′是△A′B′C′的中位线,
∴E′D′=B′C′=×4=2.
故选:A.
4.如图,已知图形是中心对称图形,则对称中心是( )
A.点C
B.点D
C.线段BC的中点
D.线段FC的中点
【解答】解:∵此图形是中心对称图形,
∴对称中心是线段FC的中点.
故选:D.
5.已知下列命题,其中正确的个数是( )
(1)关于中心对称的两个图形一定不全等;
(2)关于中心对称的两个图形是全等形;
(3)两个全等的图形一定关于中心对称.
A.0个
B.1个
C.2个
D.3个
【解答】解:关于中心对称的两个图形一定全等,两个全等的图形不一定关于中心对称.
故只有(2)说法正确,
故选:B.
6.已知△ABC和△DEF关于点O对称,相应的对称点如图所示,则下列结论正确的是( )
A.AO=BO
B.BO=EO
C.点A关于点O的对称点是点D
D.点D
在BO的延长线上
【解答】解:A、AO=OE,错误;
B、BO=DO,错误;
C、点A关于点O的对称点是点E,错误;
D、点D
在BO的延长线上,正确;
故选:D.
二.填空题(共6小题)
7.关于某一点成中心对称的两个图形,对称点的连线都经过 对称中心 ,并且被 对称中心 平分.
【解答】解:根据中心对称的性质,得
对称点的连线都经过对称中心,并且被对称中心平分.
8.如图,是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为 4 .
【解答】解:∵在Rt△ABC中,∠B=30°,AC=1,
∴AB=2AC=2,
根据中心对称的性质得到BB′=2AB=4.
故答案为:4.
9.如图,△ABC与△DEC关于点C成中心对称,则线段AB与DE的大小关系是 AB=DE .
【解答】解:∵△ABC与△DEC关于点C成中心对称,
∴AB=DE
故答案为:AB=DE.
10.如图,△ABC绕点A旋转180°,得到△A′B′C′,A为旋转中心,则△ABC与△A′B′C′关于点 A 中心对称;若∠C=90°,∠B=30°,BC=1,则BB′的长为 .
【解答】解:∵如图,△ABC绕点A旋转180°,得到△A′B′C′,A为旋转中心,
∴△ABC与△A′B′C′关于点
A中心对称;
∵在直角△ABC中,∠B=30°,BC=1,
∴AB===
∴BB′=2AB=.
故答案是:A;.
11.与电子显示的四位数6925不相等,但为全等图形的四位数是 5269 .
【解答】答:5269.
12.如图,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.在这种变换下,如果△ABC中任意一点M的坐标为(x,y),那么它们的对应点N的坐标是 (﹣x,﹣y) .
【解答】解:由图可知两三角形关于点O成中心对称,
关于原点成中心对称的坐标的特点为横纵坐标均互为相反数,
故点N的坐标是(﹣x,﹣y).
三.解答题(共3小题)
13.如图所示的两个图形成中心对称,请找出它的对称中点.
【解答】解:连接CC′,BB′,两条线段相交于当O,
则点O即为对称中点.
14.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
【解答】解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8;
(3)∵在△ABD和△CDE中,,
∴△ABD≌△CDE(SAS),
∴AB=CE,AD=DE
∵△ACE中,AC﹣AB<AE<AC+AB,
∴2<AE<8,
∴1<AD<4.
15.如图,矩形ABCD和矩形A'B'C'D关于点D成中心对称.
求证:四边形ACA'C'是菱形.
【解答】解:∵矩形ABCD与矩形AB′C′D′关于点D成中心对称,
∴∠ADC=90°,CD=CD′,DA=DA′,
∴四边形ACA'C'是平行四边形,AA′⊥CC′,
∴四边形ACA'C'是菱形.
同课章节目录
