华东师大版数学八年级上册11.1.1平方根课件(共30张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册11.1.1平方根课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 22:08:08 | ||
图片预览











文档简介
(共30张PPT)
小故事大智慧
A对B说:“我要离开这个公司,我恨这个公司!”
B建议道:“我举双手赞成你报复这破公司,一定要给它点颜色看看。不过你现在离开,还不是最好的时机。”
A问:“为什么?”
B说:“如果你现在走,公司的损失并不大。你应该趁着在公司的机会,拼命去为自己拉一些客户,成为公司独当一面的人物,然后带着这些客户突然离开公司,公司才会受到重大损失,非常被动。”
A觉得B说的非常在理,于是努力工作。事遂所愿,半年多的努力工作后,他有了许多忠实的客户。
再见面时B问A:“现在是时机了,要赶快行动哦!”
A淡然笑道:“老总跟我长谈过,准备升我做总经理助理,我暂时没有离开的打算。”其实这也正是B的初衷。一个人的工作,永远只是为自己的简历。只有付出大于得到,让老板真正看到你的能力大于位置,才会给你更多的机会替他创造更多利润。
不要一味地埋怨环境带给人的诸多不便,其实环境本身是客观存在的,谁处于那个位置都会遇到同样的问题,聪明的人会努力去改造罢了
11.1
平方根与立方根
1
平方根
第11章
数的开方
1
在动手操作过程中,感受到无理数在实际生活中大量存在,会用根号表示平方根。
2
知道平方根的概念,会求一个数的平方根。
学习目标
学习重点
平方根的概念及求某些数的平方根的方法。
正方形的面积
1
9
16
25
36
边长
1
3
4
5
6
问题:学校要举行美术作品比赛,小鸥
很高兴,他想裁出一块面积为25cm2的正
方形画布,画上自己的得意之作参加比
赛,这块正方形画布的边长应取多少?
5cm
一般地,如果一个数X的平方等于a,即X2=a那么这个数X叫做a的平方根。
例如,因为3和-3的平方都等于9,我们就说3和-3是9的平方根。也可以说:9的平方根是±3.
归纳
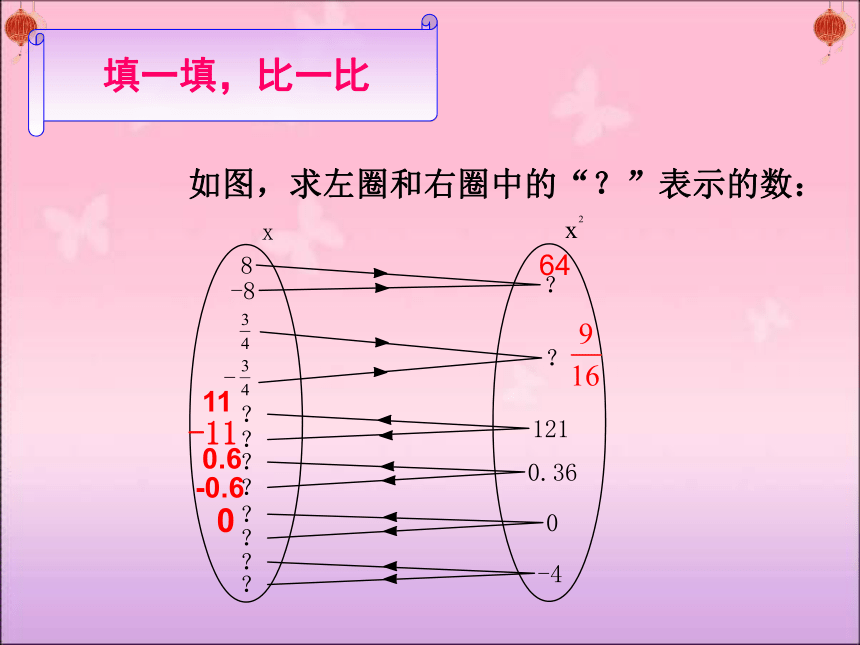
如图,求左圈和右圈中的“?”表示的数:
64
-11
11
0.6
-0.6
0
填一填,比一比
(1)一个正数有几个平方根?
(2)0
有几个平方根?
(3)负数呢?
一个正数有两个平方根,0只有一个平方根,它是0本身;负数没有平方根。
议一议:
如果一个数的平方等于a
,那么这个数叫做a
的平方根。例如:52=25所以5是25的一个平方根,(-5)2=52=25,所以-5也是25的一个平方根。
平方根的概念:
平方根的表示方法、读法
根号
被开方数
(a是非负数)
读作:正负根号a
平方根具有双值性:
正数有两个平方根,两个平方根互为相反数。
0的平方根还是0。
负数没有平方根。
0除外
例题1
例1
求100的平方根。
解:
因为102=100(-10)2=100,除了10和-10以外,任何数的平方都不等于100,
所以100的平方根是10和-10,也可以说,100的平方根是
看谁能很快记住11到20的平方?
121
144
169
196
225
256
289
324
361
400
磨拳搽掌
因为任何实数的平方都为非负数,所以负数没有算术平方根。
想一想:
负数有算术平方根吗?
小试牛刀:
的平方根是什么?
3
4
-4有没有平方根?为什么?
2
0的平方根是什么?
1
144的平方根是什么?
0
没有,因为一个数的平方不可能是负数
特殊:0的算术平方根是0。
一般地,如果一个正数x的平方等于a,即
=
a,
那么这个正数x叫做a的算术平方根。a的算术平方
根记为
,读作“根号a”,另一个平方根是它的相反数,即
,因此正数a的平方根可以记作
a叫做被开方数。
1、下列各式中哪些有意义?哪些无意义?为什么?
答:有意义的是
无意义的是
快
乐
套
餐
2、判断
(1)5是25的算术平方根;
(2)-6是
36
的算术平方根;
(3)0的算术平方根是0;
(4)0.01是0.1的算术平方根;
(5)-5是-25的算术平方根。
3.求下列各数的算术平方根
①
25
②
③
0.36
④
0
⑤
49
81
①∵52
=25,∴25的算术平方根是5,即
=5
0,1
0
正
①
正数的算术平方根是
数,0的算术平方根
是
,算术平方根等于它本身的数是
②
的算术平方根是
4
4
填空:
浅谈收获
特殊:0的算术平方根是0。
负数没有算术平方根。
求一个数a的平方根的运算,叫做开平方,其中a叫做被开方数。
可以看的出,平方与开平方互为逆运算,根据这种关系可以求出一个数的平方根.
平方与开平方有什么关系?
结论
两种运算有什么不同?
+1
-1
+2
-2
+3
-3
1
4
9
X
x2
1
4
9
+1
-1
+2
-2
+3
-3
这是什么运算?
平方运算
x2
X
合作探究
收
获
2、一个正数有两个平方根,0只有一个平方根,它是0本
身;负数没有平方根。
3、求一个数a的平方根的运算,叫做开平方,其中a叫做
被开方数。
4、平方与开平方互为逆运算。
1、
一般地,如果一个数X的平方等于a,即X2=a那么这个
数X叫做a的平方根(也叫做二次方根)。
(1)49的平方根是(
),算术平方根是(
);
(2)0.09的平方根是(
),算术平方根是(
);
(3)若-
是x的一个平方根,那么x的另一个平方
根是(
);
(4)平方根等于它本身的数是(
),算术平方根等于
它本身的数是(
);
(5)
一个数的平方等于
0.01
,这个数是(
);
(6)
(7)求下列各数的平方根:0.81,
0,
±7
±0.3
±0.1
7
0,1
0
0.3
5
±0.9
,0,
±
3
课后思考:
填表
1
16
36
49
±4
±1
±6
±7
议一议
(1)正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
探索
&
交流
1、正数有_____平方根,它们__________;
2、0的平方根是______;
3、负数__________.
0
……
0
如果一个数
X
的平方等于
a
,即X2=
a
,那么这个数
X
叫做a
的平方根(二次方根)
两个
互为相反数
0
没有平方根
……
求下列各数的平方根
1)
100
2)
3)
0.25
解:
1)
因为
(
10
)2
=100,
2)
因为(
)2=
,
3)
因为(
0.5)2
=
0.25,
所以100的平方根是
10,
所以
的平方根是
,
所以
0.25
的平方根是
0.5,
求下列各式的值:
±
(3)
解:
你知道
有多大吗?
无限不循环小数
逼近法
我爱思考
作业
课本练习
第一题
第三题
同学们!再见!
小故事大智慧
A对B说:“我要离开这个公司,我恨这个公司!”
B建议道:“我举双手赞成你报复这破公司,一定要给它点颜色看看。不过你现在离开,还不是最好的时机。”
A问:“为什么?”
B说:“如果你现在走,公司的损失并不大。你应该趁着在公司的机会,拼命去为自己拉一些客户,成为公司独当一面的人物,然后带着这些客户突然离开公司,公司才会受到重大损失,非常被动。”
A觉得B说的非常在理,于是努力工作。事遂所愿,半年多的努力工作后,他有了许多忠实的客户。
再见面时B问A:“现在是时机了,要赶快行动哦!”
A淡然笑道:“老总跟我长谈过,准备升我做总经理助理,我暂时没有离开的打算。”其实这也正是B的初衷。一个人的工作,永远只是为自己的简历。只有付出大于得到,让老板真正看到你的能力大于位置,才会给你更多的机会替他创造更多利润。
不要一味地埋怨环境带给人的诸多不便,其实环境本身是客观存在的,谁处于那个位置都会遇到同样的问题,聪明的人会努力去改造罢了
11.1
平方根与立方根
1
平方根
第11章
数的开方
1
在动手操作过程中,感受到无理数在实际生活中大量存在,会用根号表示平方根。
2
知道平方根的概念,会求一个数的平方根。
学习目标
学习重点
平方根的概念及求某些数的平方根的方法。
正方形的面积
1
9
16
25
36
边长
1
3
4
5
6
问题:学校要举行美术作品比赛,小鸥
很高兴,他想裁出一块面积为25cm2的正
方形画布,画上自己的得意之作参加比
赛,这块正方形画布的边长应取多少?
5cm
一般地,如果一个数X的平方等于a,即X2=a那么这个数X叫做a的平方根。
例如,因为3和-3的平方都等于9,我们就说3和-3是9的平方根。也可以说:9的平方根是±3.
归纳
如图,求左圈和右圈中的“?”表示的数:
64
-11
11
0.6
-0.6
0
填一填,比一比
(1)一个正数有几个平方根?
(2)0
有几个平方根?
(3)负数呢?
一个正数有两个平方根,0只有一个平方根,它是0本身;负数没有平方根。
议一议:
如果一个数的平方等于a
,那么这个数叫做a
的平方根。例如:52=25所以5是25的一个平方根,(-5)2=52=25,所以-5也是25的一个平方根。
平方根的概念:
平方根的表示方法、读法
根号
被开方数
(a是非负数)
读作:正负根号a
平方根具有双值性:
正数有两个平方根,两个平方根互为相反数。
0的平方根还是0。
负数没有平方根。
0除外
例题1
例1
求100的平方根。
解:
因为102=100(-10)2=100,除了10和-10以外,任何数的平方都不等于100,
所以100的平方根是10和-10,也可以说,100的平方根是
看谁能很快记住11到20的平方?
121
144
169
196
225
256
289
324
361
400
磨拳搽掌
因为任何实数的平方都为非负数,所以负数没有算术平方根。
想一想:
负数有算术平方根吗?
小试牛刀:
的平方根是什么?
3
4
-4有没有平方根?为什么?
2
0的平方根是什么?
1
144的平方根是什么?
0
没有,因为一个数的平方不可能是负数
特殊:0的算术平方根是0。
一般地,如果一个正数x的平方等于a,即
=
a,
那么这个正数x叫做a的算术平方根。a的算术平方
根记为
,读作“根号a”,另一个平方根是它的相反数,即
,因此正数a的平方根可以记作
a叫做被开方数。
1、下列各式中哪些有意义?哪些无意义?为什么?
答:有意义的是
无意义的是
快
乐
套
餐
2、判断
(1)5是25的算术平方根;
(2)-6是
36
的算术平方根;
(3)0的算术平方根是0;
(4)0.01是0.1的算术平方根;
(5)-5是-25的算术平方根。
3.求下列各数的算术平方根
①
25
②
③
0.36
④
0
⑤
49
81
①∵52
=25,∴25的算术平方根是5,即
=5
0,1
0
正
①
正数的算术平方根是
数,0的算术平方根
是
,算术平方根等于它本身的数是
②
的算术平方根是
4
4
填空:
浅谈收获
特殊:0的算术平方根是0。
负数没有算术平方根。
求一个数a的平方根的运算,叫做开平方,其中a叫做被开方数。
可以看的出,平方与开平方互为逆运算,根据这种关系可以求出一个数的平方根.
平方与开平方有什么关系?
结论
两种运算有什么不同?
+1
-1
+2
-2
+3
-3
1
4
9
X
x2
1
4
9
+1
-1
+2
-2
+3
-3
这是什么运算?
平方运算
x2
X
合作探究
收
获
2、一个正数有两个平方根,0只有一个平方根,它是0本
身;负数没有平方根。
3、求一个数a的平方根的运算,叫做开平方,其中a叫做
被开方数。
4、平方与开平方互为逆运算。
1、
一般地,如果一个数X的平方等于a,即X2=a那么这个
数X叫做a的平方根(也叫做二次方根)。
(1)49的平方根是(
),算术平方根是(
);
(2)0.09的平方根是(
),算术平方根是(
);
(3)若-
是x的一个平方根,那么x的另一个平方
根是(
);
(4)平方根等于它本身的数是(
),算术平方根等于
它本身的数是(
);
(5)
一个数的平方等于
0.01
,这个数是(
);
(6)
(7)求下列各数的平方根:0.81,
0,
±7
±0.3
±0.1
7
0,1
0
0.3
5
±0.9
,0,
±
3
课后思考:
填表
1
16
36
49
±4
±1
±6
±7
议一议
(1)正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
探索
&
交流
1、正数有_____平方根,它们__________;
2、0的平方根是______;
3、负数__________.
0
……
0
如果一个数
X
的平方等于
a
,即X2=
a
,那么这个数
X
叫做a
的平方根(二次方根)
两个
互为相反数
0
没有平方根
……
求下列各数的平方根
1)
100
2)
3)
0.25
解:
1)
因为
(
10
)2
=100,
2)
因为(
)2=
,
3)
因为(
0.5)2
=
0.25,
所以100的平方根是
10,
所以
的平方根是
,
所以
0.25
的平方根是
0.5,
求下列各式的值:
±
(3)
解:
你知道
有多大吗?
无限不循环小数
逼近法
我爱思考
作业
课本练习
第一题
第三题
同学们!再见!
