人教版数学七年级上册 4.3角 备课教案及同步练习(2课时 含答案)
文档属性
| 名称 | 人教版数学七年级上册 4.3角 备课教案及同步练习(2课时 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 181.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 00:00:00 | ||
图片预览




文档简介
第四章4.3角
年
级
初一
学
科
数学
版
本
人教版
课程标题
4.3角
一、学习目标:
1、理解角的概念、表示方法、测量方法和画法.
2、认识角的度量单位度、分、秒,会进行简单的换算和角度计算.
3、学会比较两个角的大小,会分析图中角的和差关系.
4、认识角的平分线及角的等分线,会画角的平分线.
二、重点、难点:
重点:角度的换算,分析角的和差关系,认识角平分线.
难点:认识复杂图形中角的和差关系,比较两个角的大小.
知识梳理
1、角
(1)定义:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两边.角也可以看作是由一条射线绕着它的端点旋转而形成的图形.
(2)表示方法:角的四种表示方法如下表:
表示方法
图示
记法
适用范围
①用三个大写字母表示
∠AOB或∠BOA
任何情况都适用,表示顶点的字母写在中间
②用一个大写字母表示
∠O
以某一点为顶点的角只有一个时
③用一个阿拉伯数字表示
∠1
任何情况都适用
④用一个希腊字母表示
∠α
任何情况都适用
(3)平角和周角:如果角的终边是由始边旋转半周而得到的(这时的始边与终边互为反向延长线),这样的角叫做平角;如果角的终边是由始边旋转一周而得到的(这时终边与始边重合),这样的角叫做周角.
2、角的度量单位及角度制
(1)角的度量单位:角的度量单位是度、分、秒,把一个周角平均分成360等份,每一份就是1°,1°的为1分,记作“1′”,1′的为1秒,记作“1″”.
(2)角度制的换算:1周角=360°,1平角=180°,1°=60′,1′=60″.
(3)角度制是60进位的,它和时间的小时、分钟、秒间的度量相类似.时钟被分成12格,相当于把圆周12等分,每一等份等于30°,时针每小时走一格为30°,每分钟走0.5°;分针每小时走一圈是360°,每分钟走6°.
3、角的比较与运算
(1)角的大小的比较方法:①叠合法;②度量法.
(2)角的和差:把两个角的一边重合,另两边在重合边的两侧,则另两边的夹角即为这两角之和;若另两边在重合边的同侧,则另两边的夹角即为两角之差.
4、角的平分线
(1)定义:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
(2)符号语言叙述:如左图所示,因为∠AOC=∠BOC,所以OC是∠AOB的平分线.反之,如果OC是∠AOB的平分线,那么∠AOC=∠BOC,并且有∠AOC=∠AOB或∠BOC=∠AOB,以及∠AOB=2∠AOC或∠AOB=2∠BOC.
(3)类似地,还有角的三等分线(如右图).
【典型例题】
知识点一:角的表示
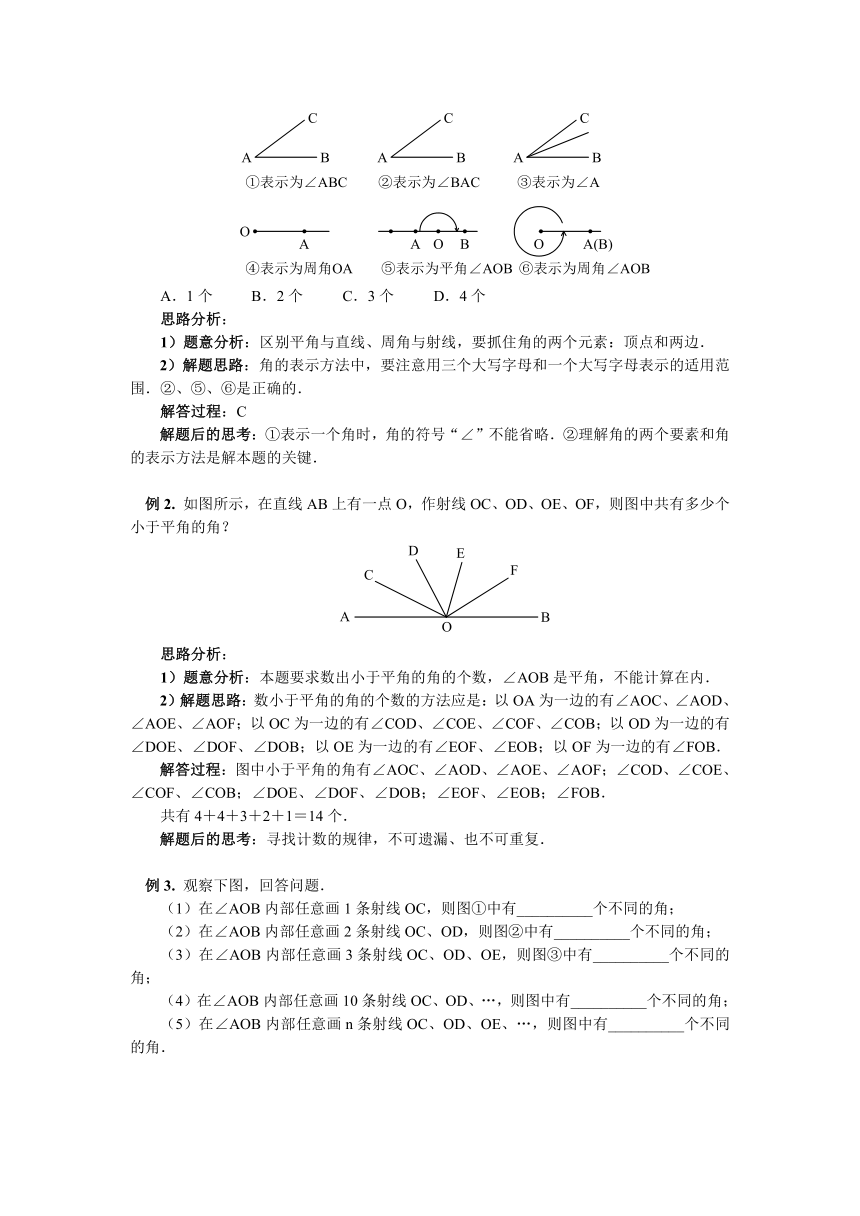
例1.
如图所示,角的表示法正确的个数是(
)
A.1个
B.2个
C.3个
D.4个
思路分析:
1)题意分析:区别平角与直线、周角与射线,要抓住角的两个元素:顶点和两边.
2)解题思路:角的表示方法中,要注意用三个大写字母和一个大写字母表示的适用范围.②、⑤、⑥是正确的.
解答过程:C
解题后的思考:①表示一个角时,角的符号“∠”不能省略.②理解角的两个要素和角的表示方法是解本题的关键.
例2.
如图所示,在直线AB上有一点O,作射线OC、OD、OE、OF,则图中共有多少个小于平角的角?
思路分析:
1)题意分析:本题要求数出小于平角的角的个数,∠AOB是平角,不能计算在内.
2)解题思路:数小于平角的角的个数的方法应是:以OA为一边的有∠AOC、∠AOD、∠AOE、∠AOF;以OC为一边的有∠COD、∠COE、∠COF、∠COB;以OD为一边的有∠DOE、∠DOF、∠DOB;以OE为一边的有∠EOF、∠EOB;以OF为一边的有∠FOB.
解答过程:图中小于平角的角有∠AOC、∠AOD、∠AOE、∠AOF;∠COD、∠COE、∠COF、∠COB;∠DOE、∠DOF、∠DOB;∠EOF、∠EOB;∠FOB.
共有4+4+3+2+1=14个.
解题后的思考:寻找计数的规律,不可遗漏、也不可重复.
例3.
观察下图,回答问题.
(1)在∠AOB内部任意画1条射线OC,则图①中有__________个不同的角;
(2)在∠AOB内部任意画2条射线OC、OD,则图②中有__________个不同的角;
(3)在∠AOB内部任意画3条射线OC、OD、OE,则图③中有__________个不同的角;
(4)在∠AOB内部任意画10条射线OC、OD、…,则图中有__________个不同的角;
(5)在∠AOB内部任意画n条射线OC、OD、OE、…,则图中有__________个不同的角.
思路分析:
1)题意分析:正确数出角的个数是解题的关键,根据角的个数,得到一列有规律的数,寻找规律,推广到一般.
2)解题思路:数角的个数时,注意不能重,也不能漏.如图①中,按逆时针方向,以OA为边的角有∠AOC,∠AOB;以OC为边的角有∠COB.共3个.
解答过程:(1)2+1=3;(2)3+2+1=6;(3)4+3+2+1=10;(4)11+10+9+…+2+1=66;(5)(n+1)+n+(n-1)+…+2+1=(n+1)(n+2).
解题后的思考:这类题与线段计数的方法类似,运用分类思想来研究问题.
小结:对角的表示方法的考查主要有两个方面:一是角的四种表示方法分别适合在什么情况下使用;二是在有规律的图形中数角的个数.
知识点二:角的比较和运算
例4.
钟表上12时15分钟时,时针与分针的夹角是(
)
A.90°
B.82.5°
C.67.5°
D.60°
思路分析:
1)题意分析:如图所示,12时15分时分针正对着数字“3”,而时针走过了数字“12”一点点.
2)解题思路:钟表上,每一个小格的度数为=6°;每一个大格的度数为=30°.
解答过程:12时15分钟时,时针偏转的角度为×30°=7.5°,分针偏转的角度为3×30°=90°,所以两针之间的夹角为90°-7.5°=82.5°.所以应选B.
解题后的思考:由本题可知分针每分钟走6°,时针每分钟走0.5°.
例5.
如图所示,将书页的一角折过去,使角的顶点落在A’处,BC为折痕,BD为∠A’BE的平分线,则∠CBD=__________.
思路分析:
1)题意分析:理解折叠的结果是∠ABC=∠CBA’=∠ABA’,即BC为∠ABA’的平分线.
2)解题思路:由BD平分∠A’BE知∠A’BD=∠A’BE,所以∠CBD=(∠ABA’+∠A’BE)=∠ABE=90°.
解答过程:90°
解题后的思考:由本题知,用折叠的方法可将一个角分成两个相等的角.
例6.
从射线OA的端点O引两条射线OB、OC,如果∠AOB=75°12′,∠BOC=26°32′.求∠AOC的度数.
思路分析:
1)题意分析:先根据题意画图,再求∠AOC的度数.
2)解题思路:∠AOB是确定的,射线OC与∠AOB有两种可能的位置关系.
解答过程:本题有两种情况,如图所示:
①OC在∠AOB的外部,
∠AOC=∠AOB+∠BOC=75°12′+26°32′=101°44′;
②OC在∠AOB的内部,
∠AOC=∠AOB-∠BOC=75°12′-26°32′=48°40′.
所以∠AOC的度数为101°44′或48°40′.
解题后的思考:考虑问题要全面.
例7.
如图所示,∠AOB=90°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
思路分析:
1)题意分析:本题应根据角的和差关系求∠MON的度数.
2)解题思路:从图中可以得到∠MON=∠MOC-∠NOC,而∠MOC=∠AOC,∠NOC=∠BOC,由此可求∠MON的度数.
解答过程:因为OM平分∠AOC,ON平分∠BOC,
所以∠MOC=∠AOC,∠NOC=∠BOC,
因为∠MON=∠MOC-∠NOC,∠AOB=90°,
所以∠MON=∠AOC-∠BOC=(∠AOC-∠BOC)=∠AOB=45°.
解题后的思考:本题中角的数量关系较复杂,解题时所分析的数据要找和已知与所求有关联的数量关系.
例8.
如图所示,已知∠AOB∶∠BOC∶∠COD=3∶2∶4,∠AOD=108°,求∠AOB、∠BOC、∠COD的度数.
思路分析:
1)题意分析:所求的三个角和已知的角∠AOD正好组成一个周角.
2)解题思路:本题中涉及到的四个角的和是周角360°,合理设出未知数,列方程求解.
解答过程:设∠AOB=3x,则∠BOC=2x,∠COD=4x,
则3x+2x+4x+108°=360°,
解得x=28°.
所以3x=84°,2x=56°,4x=112°
即∠AOB=84°,∠BOC=56°,∠COD=112°.
解题后的思考:用方程解决角的计算问题时,关键是合理设出未知数,找出相等关系,这类问题的相等关系一般是几个角的和或差等于已知角(或平角或周角等).
小结:在角的计算问题中,一般都是利用角的和差关系求角的度数,这里应重点掌握角的平分线的性质和运用.
【预习】
余角与补角(4.3.3)
一、预习新知
1、余角和补角
2、方位角
二、预习点拨
探究与反思
探究任务一:余角和补角
【反思】(1)怎样理解互为余角和互为补角?
(2)余角和补角的性质是什么?
探究任务二:方位角
【反思】(1)什么是方位角?
(2)怎样用方位角确定方向?
【练习】(答题时间:60分钟)
一、选择题.
1、如图所示,图中小于平角的角的个数是(
)
A.
3个
B.
4个
C.
5个
D.
6个
2、下列各角中,不可能是钝角的角是(
)
A.
周角
B.
平角
C.
钝角
D.
直角
3、已知射线OA、OB,能判定OC是∠AOB的平分线的是(
)
A.
∠AOC=∠BOC
B.
∠AOB=2∠AOC
C.
∠BOC=∠AOB
D.
A、B、C都能
4、如果∠1-∠2=∠3,且∠4+∠2=∠1,那么∠3和∠4间的关系是(
)
A.
∠3>∠4
B.
∠3=∠4
C.
∠3<∠4
D.
不确定
5、用一副三角板不能画出(
)
A.
75°角
B.
135°角
C.
160°角
D.
105°角
6、如图所示,若∠AOB=∠COD,那么(
)
A.
∠1>∠2
B.
∠1=∠2
C.
∠1<∠2
D.
不确定
7、在钟表上,1点30分时,时针与分针所成的角是(
)
A.
150°
B.
165°
C.
135°
D.
120°
8、如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是(
)
A.
∠COD=∠AOC
B.
∠AOD=∠AOB
C.
∠BOD=∠AOB
D.
∠BOC=∠AOB
二、填空题.
9、如图所示,把图中用数字表示的角,改用大写字母表示分别是__________.
10、()°=__________′=__________″;6000″=__________′=__________°.
11、如果∠1=∠2,∠1+∠3=90°,则∠2+∠3=__________.
12、如图所示,用“=”或“>”或“<”填空:
(1)∠AOC_______∠AOB+∠BOC;(2)∠AOC_______∠AOB;(3)∠BOD-∠BOC______∠DOC;(4)∠AOD______∠AOC+∠BOD.
13、时钟从3点10分走到3点35分,它的分针转过__________度.
14、如下图,OC平分∠AOB,OD平分∠AOC,则图中相等的角有__________;∠AOD=______∠AOC=______∠AOB.
三、解答题.
15、计算:(1)49°38′+66°22′;(2)180°-79°19′;(3)22°16′×5.
16、把一个周角7等分,每一等份是多少度的角?(精确到分)
17、如下图,分别确定四个城市相应钟表上时针与分针所成角的度数.
18、如下图,已知OB平分∠AOC,OD平分∠COE,∠AOC=80°,∠DOE=30°.求(1)∠AOB;(2)∠COD;(3)∠BOD.
19、如下图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠COD的3倍,求∠AOB的度数.
20、(1)如图所示,已知∠AOB=90°,∠BOC=30°.OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
(2)如果(1)中∠AOB=∠α,其他条件不变,求∠MON的度数.
(3)你从(1)、(2)的结果中能发现什么规律?
一、选择题:
1、C
2、D
3、A
4、B
5、C
6、B
7、C
解析:1点30分时,分针正对着数字“6”,时针在数字“1”和“2”正中间,此时时针与分针所成的角是135°.
8、A
解析:根据题意,∠COD=∠BOC,又因为∠BOC=∠AOC,所以∠COD=∠AOC.所以选A.选项B、C、D不一定成立.
二、填空题:
9、∠ADE,∠BDE,∠CED,∠B,∠AED
10、7.5′
450″
100′
()
11、90°
12、(1)=(2)>(3)=(4)<
13、150
解析:分针从3点10分走到3点35分,共走过了25分钟,转过的角度是360°×=150°.
14、∠AOC=∠BOC、∠AOD=∠COD,
三、解答题:
15、解:(1)原式=115°60′=116°;(2)原式=100°41′;(3)原式=110°80′=111°20′.
16、解:根据题意,360°÷7≈51°26′.
17、解:巴黎时间是1点整,时针与分针所成的角是:360°×=30°;伦敦时间是12点整,时针与分针所成的角是0°;北京时间是8点整,时针与分针所成的角是30°×4=120°;东京时间是9点整,时针与分针所成的角是30°×3=90°.
18、解:(1)∠AOB=∠AOC=40°;(2)∠COD=∠DOE=30°;(3)∠BOD=∠COD+∠BOC=∠COD+∠AOB=70°
19、解:∠AOB=∠BOD+∠AOD=∠BOD+∠AOC-∠COD.因为∠AOC=60°,∠BOD=90°,所以∠AOB=90°+60°-∠COD.又因为∠AOB是∠COD的3倍,所以∠COD=∠AOB.所以∠AOB=90°+60°-∠AOB.解得∠AOB=112.5°.
20、解:(1)因为OM平分∠AOC,ON平分∠BOC,所以∠MOC=∠AOC,∠NOC=∠BOC.所以∠MON=∠MOC-∠NOC=∠AOC-∠BOC=(∠AOC-∠BOC)=∠AOB.因为∠AOB=90°,所以∠MON=45°.
(2)当∠AOB=∠α,其他条件不变时,总有∠MON=∠AOB=.
(3)由(1)、(2)的结果和(1)的解答过程,可以得出结论:∠MON的大小与∠BOC的大小无关,它总等于∠AOB的一半.
年
级
初一
学
科
数学
版
本
人教版
课程标题
4.3角
一、学习目标:
1、理解角的概念、表示方法、测量方法和画法.
2、认识角的度量单位度、分、秒,会进行简单的换算和角度计算.
3、学会比较两个角的大小,会分析图中角的和差关系.
4、认识角的平分线及角的等分线,会画角的平分线.
二、重点、难点:
重点:角度的换算,分析角的和差关系,认识角平分线.
难点:认识复杂图形中角的和差关系,比较两个角的大小.
知识梳理
1、角
(1)定义:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两边.角也可以看作是由一条射线绕着它的端点旋转而形成的图形.
(2)表示方法:角的四种表示方法如下表:
表示方法
图示
记法
适用范围
①用三个大写字母表示
∠AOB或∠BOA
任何情况都适用,表示顶点的字母写在中间
②用一个大写字母表示
∠O
以某一点为顶点的角只有一个时
③用一个阿拉伯数字表示
∠1
任何情况都适用
④用一个希腊字母表示
∠α
任何情况都适用
(3)平角和周角:如果角的终边是由始边旋转半周而得到的(这时的始边与终边互为反向延长线),这样的角叫做平角;如果角的终边是由始边旋转一周而得到的(这时终边与始边重合),这样的角叫做周角.
2、角的度量单位及角度制
(1)角的度量单位:角的度量单位是度、分、秒,把一个周角平均分成360等份,每一份就是1°,1°的为1分,记作“1′”,1′的为1秒,记作“1″”.
(2)角度制的换算:1周角=360°,1平角=180°,1°=60′,1′=60″.
(3)角度制是60进位的,它和时间的小时、分钟、秒间的度量相类似.时钟被分成12格,相当于把圆周12等分,每一等份等于30°,时针每小时走一格为30°,每分钟走0.5°;分针每小时走一圈是360°,每分钟走6°.
3、角的比较与运算
(1)角的大小的比较方法:①叠合法;②度量法.
(2)角的和差:把两个角的一边重合,另两边在重合边的两侧,则另两边的夹角即为这两角之和;若另两边在重合边的同侧,则另两边的夹角即为两角之差.
4、角的平分线
(1)定义:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
(2)符号语言叙述:如左图所示,因为∠AOC=∠BOC,所以OC是∠AOB的平分线.反之,如果OC是∠AOB的平分线,那么∠AOC=∠BOC,并且有∠AOC=∠AOB或∠BOC=∠AOB,以及∠AOB=2∠AOC或∠AOB=2∠BOC.
(3)类似地,还有角的三等分线(如右图).
【典型例题】
知识点一:角的表示
例1.
如图所示,角的表示法正确的个数是(
)
A.1个
B.2个
C.3个
D.4个
思路分析:
1)题意分析:区别平角与直线、周角与射线,要抓住角的两个元素:顶点和两边.
2)解题思路:角的表示方法中,要注意用三个大写字母和一个大写字母表示的适用范围.②、⑤、⑥是正确的.
解答过程:C
解题后的思考:①表示一个角时,角的符号“∠”不能省略.②理解角的两个要素和角的表示方法是解本题的关键.
例2.
如图所示,在直线AB上有一点O,作射线OC、OD、OE、OF,则图中共有多少个小于平角的角?
思路分析:
1)题意分析:本题要求数出小于平角的角的个数,∠AOB是平角,不能计算在内.
2)解题思路:数小于平角的角的个数的方法应是:以OA为一边的有∠AOC、∠AOD、∠AOE、∠AOF;以OC为一边的有∠COD、∠COE、∠COF、∠COB;以OD为一边的有∠DOE、∠DOF、∠DOB;以OE为一边的有∠EOF、∠EOB;以OF为一边的有∠FOB.
解答过程:图中小于平角的角有∠AOC、∠AOD、∠AOE、∠AOF;∠COD、∠COE、∠COF、∠COB;∠DOE、∠DOF、∠DOB;∠EOF、∠EOB;∠FOB.
共有4+4+3+2+1=14个.
解题后的思考:寻找计数的规律,不可遗漏、也不可重复.
例3.
观察下图,回答问题.
(1)在∠AOB内部任意画1条射线OC,则图①中有__________个不同的角;
(2)在∠AOB内部任意画2条射线OC、OD,则图②中有__________个不同的角;
(3)在∠AOB内部任意画3条射线OC、OD、OE,则图③中有__________个不同的角;
(4)在∠AOB内部任意画10条射线OC、OD、…,则图中有__________个不同的角;
(5)在∠AOB内部任意画n条射线OC、OD、OE、…,则图中有__________个不同的角.
思路分析:
1)题意分析:正确数出角的个数是解题的关键,根据角的个数,得到一列有规律的数,寻找规律,推广到一般.
2)解题思路:数角的个数时,注意不能重,也不能漏.如图①中,按逆时针方向,以OA为边的角有∠AOC,∠AOB;以OC为边的角有∠COB.共3个.
解答过程:(1)2+1=3;(2)3+2+1=6;(3)4+3+2+1=10;(4)11+10+9+…+2+1=66;(5)(n+1)+n+(n-1)+…+2+1=(n+1)(n+2).
解题后的思考:这类题与线段计数的方法类似,运用分类思想来研究问题.
小结:对角的表示方法的考查主要有两个方面:一是角的四种表示方法分别适合在什么情况下使用;二是在有规律的图形中数角的个数.
知识点二:角的比较和运算
例4.
钟表上12时15分钟时,时针与分针的夹角是(
)
A.90°
B.82.5°
C.67.5°
D.60°
思路分析:
1)题意分析:如图所示,12时15分时分针正对着数字“3”,而时针走过了数字“12”一点点.
2)解题思路:钟表上,每一个小格的度数为=6°;每一个大格的度数为=30°.
解答过程:12时15分钟时,时针偏转的角度为×30°=7.5°,分针偏转的角度为3×30°=90°,所以两针之间的夹角为90°-7.5°=82.5°.所以应选B.
解题后的思考:由本题可知分针每分钟走6°,时针每分钟走0.5°.
例5.
如图所示,将书页的一角折过去,使角的顶点落在A’处,BC为折痕,BD为∠A’BE的平分线,则∠CBD=__________.
思路分析:
1)题意分析:理解折叠的结果是∠ABC=∠CBA’=∠ABA’,即BC为∠ABA’的平分线.
2)解题思路:由BD平分∠A’BE知∠A’BD=∠A’BE,所以∠CBD=(∠ABA’+∠A’BE)=∠ABE=90°.
解答过程:90°
解题后的思考:由本题知,用折叠的方法可将一个角分成两个相等的角.
例6.
从射线OA的端点O引两条射线OB、OC,如果∠AOB=75°12′,∠BOC=26°32′.求∠AOC的度数.
思路分析:
1)题意分析:先根据题意画图,再求∠AOC的度数.
2)解题思路:∠AOB是确定的,射线OC与∠AOB有两种可能的位置关系.
解答过程:本题有两种情况,如图所示:
①OC在∠AOB的外部,
∠AOC=∠AOB+∠BOC=75°12′+26°32′=101°44′;
②OC在∠AOB的内部,
∠AOC=∠AOB-∠BOC=75°12′-26°32′=48°40′.
所以∠AOC的度数为101°44′或48°40′.
解题后的思考:考虑问题要全面.
例7.
如图所示,∠AOB=90°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
思路分析:
1)题意分析:本题应根据角的和差关系求∠MON的度数.
2)解题思路:从图中可以得到∠MON=∠MOC-∠NOC,而∠MOC=∠AOC,∠NOC=∠BOC,由此可求∠MON的度数.
解答过程:因为OM平分∠AOC,ON平分∠BOC,
所以∠MOC=∠AOC,∠NOC=∠BOC,
因为∠MON=∠MOC-∠NOC,∠AOB=90°,
所以∠MON=∠AOC-∠BOC=(∠AOC-∠BOC)=∠AOB=45°.
解题后的思考:本题中角的数量关系较复杂,解题时所分析的数据要找和已知与所求有关联的数量关系.
例8.
如图所示,已知∠AOB∶∠BOC∶∠COD=3∶2∶4,∠AOD=108°,求∠AOB、∠BOC、∠COD的度数.
思路分析:
1)题意分析:所求的三个角和已知的角∠AOD正好组成一个周角.
2)解题思路:本题中涉及到的四个角的和是周角360°,合理设出未知数,列方程求解.
解答过程:设∠AOB=3x,则∠BOC=2x,∠COD=4x,
则3x+2x+4x+108°=360°,
解得x=28°.
所以3x=84°,2x=56°,4x=112°
即∠AOB=84°,∠BOC=56°,∠COD=112°.
解题后的思考:用方程解决角的计算问题时,关键是合理设出未知数,找出相等关系,这类问题的相等关系一般是几个角的和或差等于已知角(或平角或周角等).
小结:在角的计算问题中,一般都是利用角的和差关系求角的度数,这里应重点掌握角的平分线的性质和运用.
【预习】
余角与补角(4.3.3)
一、预习新知
1、余角和补角
2、方位角
二、预习点拨
探究与反思
探究任务一:余角和补角
【反思】(1)怎样理解互为余角和互为补角?
(2)余角和补角的性质是什么?
探究任务二:方位角
【反思】(1)什么是方位角?
(2)怎样用方位角确定方向?
【练习】(答题时间:60分钟)
一、选择题.
1、如图所示,图中小于平角的角的个数是(
)
A.
3个
B.
4个
C.
5个
D.
6个
2、下列各角中,不可能是钝角的角是(
)
A.
周角
B.
平角
C.
钝角
D.
直角
3、已知射线OA、OB,能判定OC是∠AOB的平分线的是(
)
A.
∠AOC=∠BOC
B.
∠AOB=2∠AOC
C.
∠BOC=∠AOB
D.
A、B、C都能
4、如果∠1-∠2=∠3,且∠4+∠2=∠1,那么∠3和∠4间的关系是(
)
A.
∠3>∠4
B.
∠3=∠4
C.
∠3<∠4
D.
不确定
5、用一副三角板不能画出(
)
A.
75°角
B.
135°角
C.
160°角
D.
105°角
6、如图所示,若∠AOB=∠COD,那么(
)
A.
∠1>∠2
B.
∠1=∠2
C.
∠1<∠2
D.
不确定
7、在钟表上,1点30分时,时针与分针所成的角是(
)
A.
150°
B.
165°
C.
135°
D.
120°
8、如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是(
)
A.
∠COD=∠AOC
B.
∠AOD=∠AOB
C.
∠BOD=∠AOB
D.
∠BOC=∠AOB
二、填空题.
9、如图所示,把图中用数字表示的角,改用大写字母表示分别是__________.
10、()°=__________′=__________″;6000″=__________′=__________°.
11、如果∠1=∠2,∠1+∠3=90°,则∠2+∠3=__________.
12、如图所示,用“=”或“>”或“<”填空:
(1)∠AOC_______∠AOB+∠BOC;(2)∠AOC_______∠AOB;(3)∠BOD-∠BOC______∠DOC;(4)∠AOD______∠AOC+∠BOD.
13、时钟从3点10分走到3点35分,它的分针转过__________度.
14、如下图,OC平分∠AOB,OD平分∠AOC,则图中相等的角有__________;∠AOD=______∠AOC=______∠AOB.
三、解答题.
15、计算:(1)49°38′+66°22′;(2)180°-79°19′;(3)22°16′×5.
16、把一个周角7等分,每一等份是多少度的角?(精确到分)
17、如下图,分别确定四个城市相应钟表上时针与分针所成角的度数.
18、如下图,已知OB平分∠AOC,OD平分∠COE,∠AOC=80°,∠DOE=30°.求(1)∠AOB;(2)∠COD;(3)∠BOD.
19、如下图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠COD的3倍,求∠AOB的度数.
20、(1)如图所示,已知∠AOB=90°,∠BOC=30°.OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
(2)如果(1)中∠AOB=∠α,其他条件不变,求∠MON的度数.
(3)你从(1)、(2)的结果中能发现什么规律?
一、选择题:
1、C
2、D
3、A
4、B
5、C
6、B
7、C
解析:1点30分时,分针正对着数字“6”,时针在数字“1”和“2”正中间,此时时针与分针所成的角是135°.
8、A
解析:根据题意,∠COD=∠BOC,又因为∠BOC=∠AOC,所以∠COD=∠AOC.所以选A.选项B、C、D不一定成立.
二、填空题:
9、∠ADE,∠BDE,∠CED,∠B,∠AED
10、7.5′
450″
100′
()
11、90°
12、(1)=(2)>(3)=(4)<
13、150
解析:分针从3点10分走到3点35分,共走过了25分钟,转过的角度是360°×=150°.
14、∠AOC=∠BOC、∠AOD=∠COD,
三、解答题:
15、解:(1)原式=115°60′=116°;(2)原式=100°41′;(3)原式=110°80′=111°20′.
16、解:根据题意,360°÷7≈51°26′.
17、解:巴黎时间是1点整,时针与分针所成的角是:360°×=30°;伦敦时间是12点整,时针与分针所成的角是0°;北京时间是8点整,时针与分针所成的角是30°×4=120°;东京时间是9点整,时针与分针所成的角是30°×3=90°.
18、解:(1)∠AOB=∠AOC=40°;(2)∠COD=∠DOE=30°;(3)∠BOD=∠COD+∠BOC=∠COD+∠AOB=70°
19、解:∠AOB=∠BOD+∠AOD=∠BOD+∠AOC-∠COD.因为∠AOC=60°,∠BOD=90°,所以∠AOB=90°+60°-∠COD.又因为∠AOB是∠COD的3倍,所以∠COD=∠AOB.所以∠AOB=90°+60°-∠AOB.解得∠AOB=112.5°.
20、解:(1)因为OM平分∠AOC,ON平分∠BOC,所以∠MOC=∠AOC,∠NOC=∠BOC.所以∠MON=∠MOC-∠NOC=∠AOC-∠BOC=(∠AOC-∠BOC)=∠AOB.因为∠AOB=90°,所以∠MON=45°.
(2)当∠AOB=∠α,其他条件不变时,总有∠MON=∠AOB=.
(3)由(1)、(2)的结果和(1)的解答过程,可以得出结论:∠MON的大小与∠BOC的大小无关,它总等于∠AOB的一半.
