人教版八年级数学上册11.1.1 三角形的边同步练习(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册11.1.1 三角形的边同步练习(Word版 含答案) | 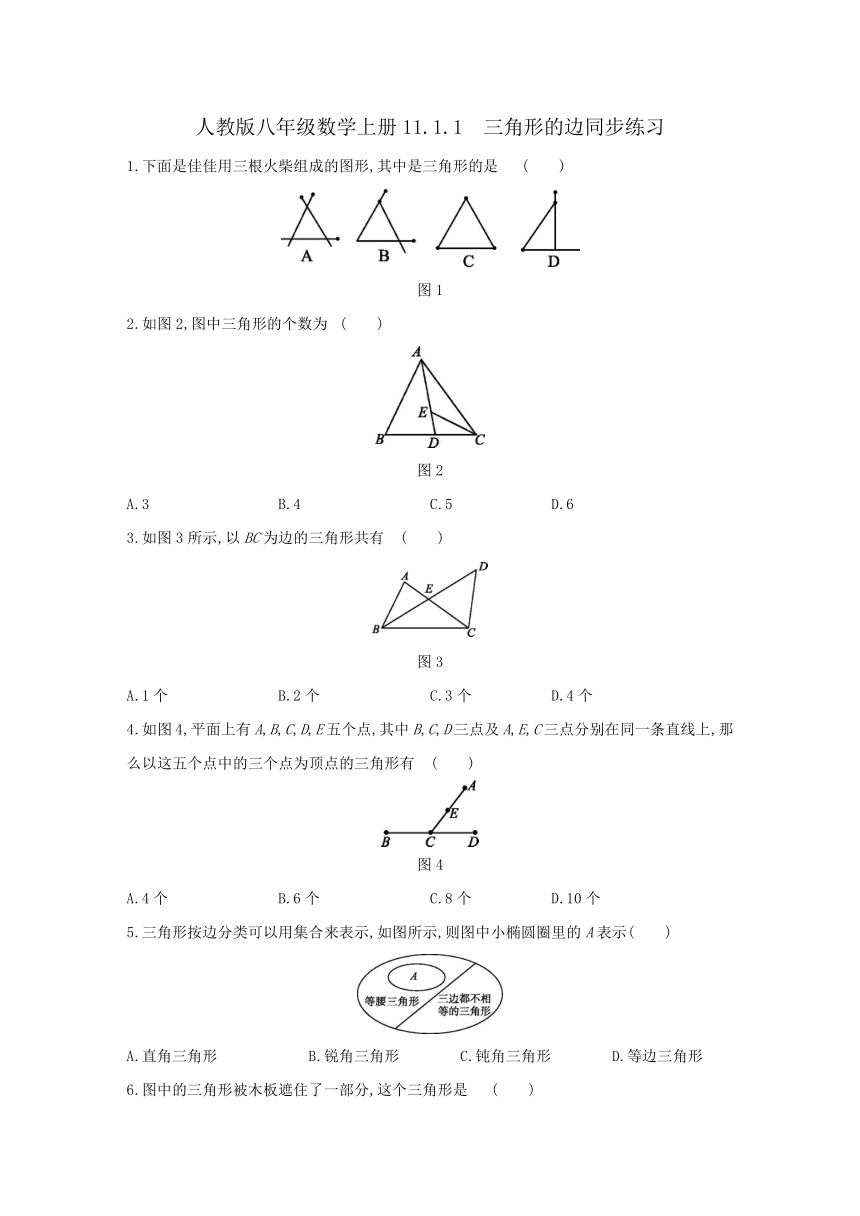 | |
| 格式 | zip | ||
| 文件大小 | 174.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 17:22:57 | ||
图片预览


文档简介
人教版八年级数学上册11.1.1 三角形的边同步练习
1.下面是佳佳用三根火柴组成的图形,其中是三角形的是
( )
图1
2.如图2,图中三角形的个数为
( )
图2
A.3
B.4
C.5
D.6
3.如图3所示,以BC为边的三角形共有
( )
图3
A.1个
B.2个
C.3个
D.4个
4.如图4,平面上有A,B,C,D,E五个点,其中B,C,D三点及A,E,C三点分别在同一条直线上,那么以这五个点中的三个点为顶点的三角形有
( )
图4
A.4个
B.6个
C.8个
D.10个
5.三角形按边分类可以用集合来表示,如图所示,则图中小椭圆圈里的A表示( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
6.图中的三角形被木板遮住了一部分,这个三角形是
( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
7.下列说法正确的是
( )
A.一个钝角三角形一定不是等腰三角形,也一定不是等边三角形
B.一个等腰三角形一定是锐角三角形或直角三角形
C.一个直角三角形一定不是等腰三角形,也一定不是等边三角形
D.一个等边三角形一定不是钝角三角形,也一定不是直角三角形
8.下列长度的三条线段,能组成三角形的是
( )
A.4
cm,5
cm,9
cm
B.8
cm,8
cm,15
cm
C.5
cm,5
cm,10
cm
D.6
cm,7
cm,14
cm
9.若一个三角形其中两边的长分别为2和4,则该三角形的周长可能是
( )
A.6
B.7
C.11
D.12
10.王师傅想做一个三角形的框架,他有两根长度分别为11
cm和12
cm的细木条,需要将其中一根木条分为两段,如果不考虑损耗和接头部分,那么他可以把哪根木条分为两段
( )
A.长度为11
cm的木条
B.长度为12
cm的木条
C.两根都可以
D.两根都不行
11.如图8,x的值可能是
( )
图8
A.11
B.12
C.13
D.14
12.一个等腰三角形两边的长分别为4,8,则它的周长为
( )
A.12
B.16
C.20
D.16或20
13.在△ABC中,∠C>∠B,AC=10,BC=6,AB=x,则x的取值范围是
( )
A.4B.10C.4D.1014.如果依次用a1,a2,a3,a4表示图①②③④中三角形的个数,那么a1=3,a2=8,a3=15,a4= .如果按照图中规律继续画图,那么a9与a8之间的关系是a9=a8+ .?
15.已知a,b,c为△ABC的三边长,化简:|a-b-c|+|b-a-c|.
16.如图9,在四边形ABCD内找一点O,使OA+OB+OC+OD的值最小,并说明理由.
图9
17.观察并探求下列各问题.
(1)如图10①,在△ABC中,P为边BC上一点,试观察比较BP+PC与AB+AC的大小,并说明理由;
(2)将(1)中点P移至△ABC内,如图②,试观察比较△BPC的周长与△ABC的周长的大小,并说明理由;
(3)将(2)中点P变为两个点P1,P2,如图③,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由;
(4)若将(3)中的四边形BP1P2C的顶点B,C移至△ABC内,得到四边形B1P1P2C1,如图④,试观察比较四边形B1P1P2C1的周长与△ABC的周长的大小,并说明理由.
图10
答案
1——13
CCCCD
DDBCB
DCB
14.24 19
15.解:由题意知a原式=|a-(b+c)|+|b-(a+c)|
=(b+c)-a+(a+c)-b
=2c.
16.解:要使OA+OB+OC+OD的值最小,则O是线段AC,BD的交点.
理由如下:在四边形ABCD内找不同于点O的任意一点P,如图,连接PA,PB,PC,PD,那么PA+PC>AC,
即PA+PC>OA+OC.
同理,PB+PD>OB+OD.
∴PA+PB+PC+PD>OA+OB+OC+OD,
即O是线段AC,BD的交点时,OA+OB+OC+OD的值最小.
17.解:(1)BP+PC(2)△BPC的周长<△ABC的周长.
理由:如图①,延长BP交AC于点M.
在△ABM中,BP+PM在△PMC中,PC将以上两式左右两边分别相加得BP+PC故BP+PC+BC即△BPC的周长<△ABC的周长.
(3)四边形BP1P2C的周长<△ABC的周长.
理由:如图②,分别延长BP1,CP2交于点M.
由(2)知,BM+CM又P1P2可得BP1+P1P2+P2C故BP1+P1P2+P2C+BC即四边形BP1P2C的周长<△ABC的周长.
(4)四边形B1P1P2C1的周长<△ABC的周长.理由:分别作如图③所示的延长线交△ABC的边于点M,N,K,H.
在△BNM中,NB1+B1P1+P1M又显然有B1C1+C1KC1P2+P2HP1P2将以上各式左右两边分别相加,得B1P1+P1P2+C1P2+B1C1即四边形B1P1P2C1的周长<△ABC的周长.
1.下面是佳佳用三根火柴组成的图形,其中是三角形的是
( )
图1
2.如图2,图中三角形的个数为
( )
图2
A.3
B.4
C.5
D.6
3.如图3所示,以BC为边的三角形共有
( )
图3
A.1个
B.2个
C.3个
D.4个
4.如图4,平面上有A,B,C,D,E五个点,其中B,C,D三点及A,E,C三点分别在同一条直线上,那么以这五个点中的三个点为顶点的三角形有
( )
图4
A.4个
B.6个
C.8个
D.10个
5.三角形按边分类可以用集合来表示,如图所示,则图中小椭圆圈里的A表示( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
6.图中的三角形被木板遮住了一部分,这个三角形是
( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
7.下列说法正确的是
( )
A.一个钝角三角形一定不是等腰三角形,也一定不是等边三角形
B.一个等腰三角形一定是锐角三角形或直角三角形
C.一个直角三角形一定不是等腰三角形,也一定不是等边三角形
D.一个等边三角形一定不是钝角三角形,也一定不是直角三角形
8.下列长度的三条线段,能组成三角形的是
( )
A.4
cm,5
cm,9
cm
B.8
cm,8
cm,15
cm
C.5
cm,5
cm,10
cm
D.6
cm,7
cm,14
cm
9.若一个三角形其中两边的长分别为2和4,则该三角形的周长可能是
( )
A.6
B.7
C.11
D.12
10.王师傅想做一个三角形的框架,他有两根长度分别为11
cm和12
cm的细木条,需要将其中一根木条分为两段,如果不考虑损耗和接头部分,那么他可以把哪根木条分为两段
( )
A.长度为11
cm的木条
B.长度为12
cm的木条
C.两根都可以
D.两根都不行
11.如图8,x的值可能是
( )
图8
A.11
B.12
C.13
D.14
12.一个等腰三角形两边的长分别为4,8,则它的周长为
( )
A.12
B.16
C.20
D.16或20
13.在△ABC中,∠C>∠B,AC=10,BC=6,AB=x,则x的取值范围是
( )
A.4
15.已知a,b,c为△ABC的三边长,化简:|a-b-c|+|b-a-c|.
16.如图9,在四边形ABCD内找一点O,使OA+OB+OC+OD的值最小,并说明理由.
图9
17.观察并探求下列各问题.
(1)如图10①,在△ABC中,P为边BC上一点,试观察比较BP+PC与AB+AC的大小,并说明理由;
(2)将(1)中点P移至△ABC内,如图②,试观察比较△BPC的周长与△ABC的周长的大小,并说明理由;
(3)将(2)中点P变为两个点P1,P2,如图③,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由;
(4)若将(3)中的四边形BP1P2C的顶点B,C移至△ABC内,得到四边形B1P1P2C1,如图④,试观察比较四边形B1P1P2C1的周长与△ABC的周长的大小,并说明理由.
图10
答案
1——13
CCCCD
DDBCB
DCB
14.24 19
15.解:由题意知a
=(b+c)-a+(a+c)-b
=2c.
16.解:要使OA+OB+OC+OD的值最小,则O是线段AC,BD的交点.
理由如下:在四边形ABCD内找不同于点O的任意一点P,如图,连接PA,PB,PC,PD,那么PA+PC>AC,
即PA+PC>OA+OC.
同理,PB+PD>OB+OD.
∴PA+PB+PC+PD>OA+OB+OC+OD,
即O是线段AC,BD的交点时,OA+OB+OC+OD的值最小.
17.解:(1)BP+PC
理由:如图①,延长BP交AC于点M.
在△ABM中,BP+PM
(3)四边形BP1P2C的周长<△ABC的周长.
理由:如图②,分别延长BP1,CP2交于点M.
由(2)知,BM+CM
(4)四边形B1P1P2C1的周长<△ABC的周长.理由:分别作如图③所示的延长线交△ABC的边于点M,N,K,H.
在△BNM中,NB1+B1P1+P1M
