湘教版九年级数学上册第4章锐角三角函数检测题(word版含答案)
文档属性
| 名称 | 湘教版九年级数学上册第4章锐角三角函数检测题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 607.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 00:00:00 | ||
图片预览



文档简介
第4章 单元检测题
(时间:100分钟 满分:120分)
一、选择题(本题共12小题,每题3分,共36分)
1.计算:sin60°·tan30°=(
)
A.1
B.
C.
D.2
2.在Rt△ABC中,∠C=90°,如果AC=4,BC=3,那么∠A的正切值为(
)
A.
B.
C.
D.
3.在△ABC中,∠C=90°,AC=4,cos
A=,那么AB的长是(
)
A.5
B.6
C.8
D.9
4.如图,为测量河两岸相对两电线杆A,B间的距离,在距A点16
m的C处(AC⊥AB),测得∠ACB=52°,则A,B之间的距离应为(
)
A.16sin52°
m
B.16cos52°
m
C.16tan52°
m
D.
m
eq
\o(\s\up7(),\s\do5(第4题图))
eq
\o(\s\up7(),\s\do5(第5题图))
eq
\o(\s\up7(),\s\do5(第6题图))
eq
\o(\s\up7(),\s\do5(第7题图))
5.如图,在△ABC中,∠C=90°,cos
A=,则sin
B=(
)
A.
B.
C.
D.
6.如图所示,△ABC在正方形网格中的位置如图示(A,B,C均在格点上),AD⊥BC于点D.下列四个选项中正确的是(
)
A.sin
α=cos
α
B.sin
α=tan
α
C.sin
β=cos
β
D.sin
β=tan
β
7.为了方便行人推车过某天桥,市政府在10
m高的天桥一侧修建了40
m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是(
)
A.
B.
C.
D.
8.若锐角三角函数tan55°=a,则a的范围是(
)
A.0<a<1
B.1<a<2
C.2<a<3
D.3<a<4
9.如果sin2α+cos230°=1,那么锐角α的度数是(
)
A.30°
B.45°
C.60°
D.90°
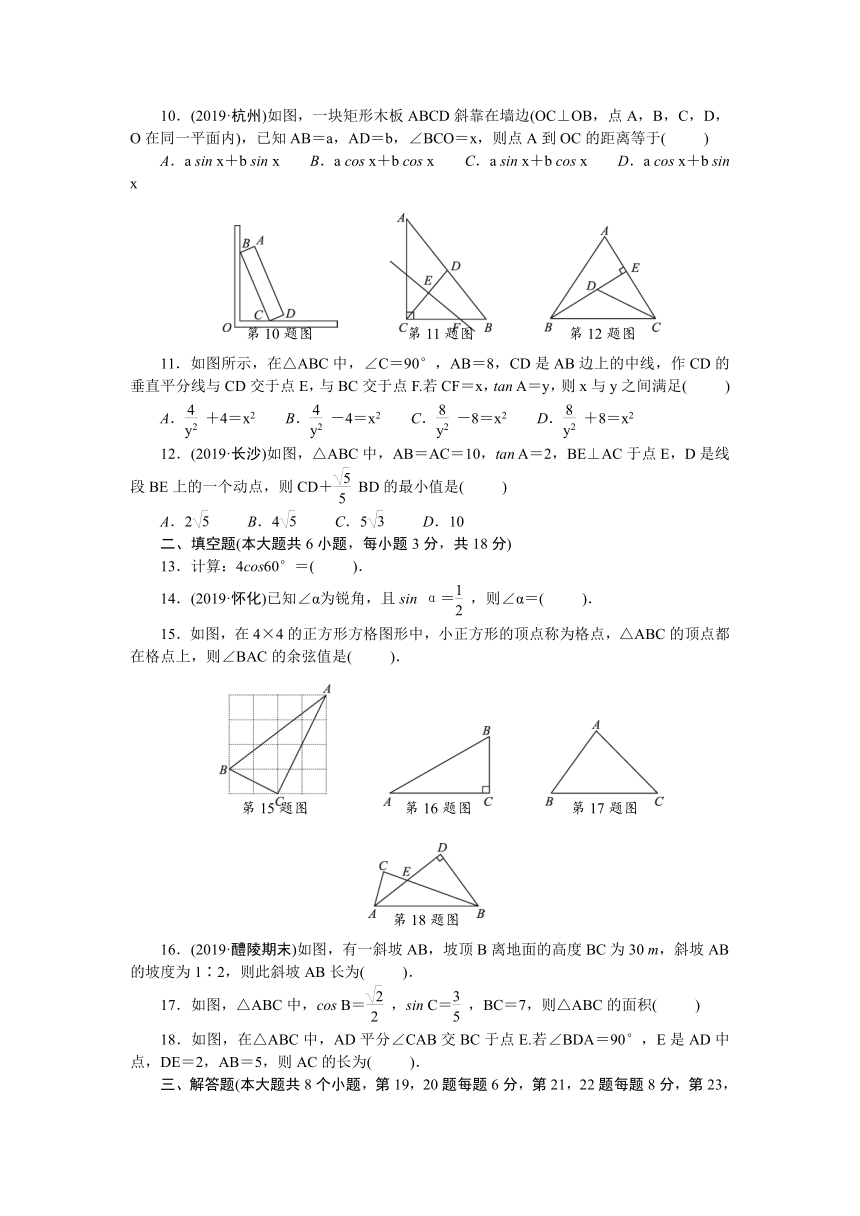
10.(2019·杭州)如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于(
)
A.a
sin
x+b
sin
x
B.a
cos
x+b
cos
x
C.a
sin
x+b
cos
x
D.a
cos
x+b
sin
x
eq
\o(\s\up7(),\s\do5(第10题图))
eq
\o(\s\up7(),\s\do5(第11题图))
eq
\o(\s\up7(),\s\do5(第12题图))
11.如图所示,在△ABC中,∠C=90°,AB=8,CD是AB边上的中线,作CD的垂直平分线与CD交于点E,与BC交于点F.若CF=x,tan
A=y,则x与y之间满足(
)
A.+4=x2
B.-4=x2
C.-8=x2
D.+8=x2
12.(2019·长沙)如图,△ABC中,AB=AC=10,tan
A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是(
)
A.2
B.4
C.5
D.10
二、填空题(本大题共6小题,每小题3分,共18分)
13.计算:4cos60°=(
).
14.(2019·怀化)已知∠α为锐角,且sin
α=,则∠α=(
).
15.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的余弦值是(
).
eq
\o(\s\up7(),\s\do5(第15题图))
eq
\o(\s\up7(),\s\do5(第16题图))
eq
\o(\s\up7(),\s\do5(第17题图))
eq
\o(\s\up7(),\s\do5(第18题图))
16.(2019·醴陵期末)如图,有一斜坡AB,坡顶B离地面的高度BC为30
m,斜坡AB的坡度为1∶2,则此斜坡AB长为(
).
17.如图,△ABC中,cos
B=,sin
C=,BC=7,则△ABC的面积(
)
18.如图,在△ABC中,AD平分∠CAB交BC于点E.若∠BDA=90°,E是AD中点,DE=2,AB=5,则AC的长为(
).
三、解答题(本大题共8个小题,第19,20题每题6分,第21,22题每题8分,第23,24题每题9分,第25,26题每题10分,共66分.解答应写出必要的文字说明、证明过程或验算步骤)
19.计算:2cos60°+4sin60°·tan30°-6cos245°.
20.在Rt△ABC中,∠C=90°,a=,b=,解这个直角三角形.
21.在一个Rt△ABC中,∠C=90°,当∠A=30°时,∠A的对边与斜边的比都等于,是一个固定值;当∠A=45°时,∠A的对边与斜边的比都等于,也是一个固定值,这就引发我们产生这样一个疑问;当∠A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值?
探究:任意画Rt△ABC和Rt△A′B′C′,使得∠C=∠C′=90°,∠A=∠A′=a,那么与有什么关系,你能解释一下吗?
22.(2019·西藏)由我国完全自主设计,自主建造的首艘国产航母于2018年5月成功完成首次海上试验任务.如图,航母由西向东航行,到达B处时,测得小岛A在北偏东60°方向上,航行20海里到达C点,这时测得小岛A在北偏东30°方向上,小岛A周围10海里内有暗礁,如果航母不改变航线继续向东航行,有没有触礁危险?请说明理由.
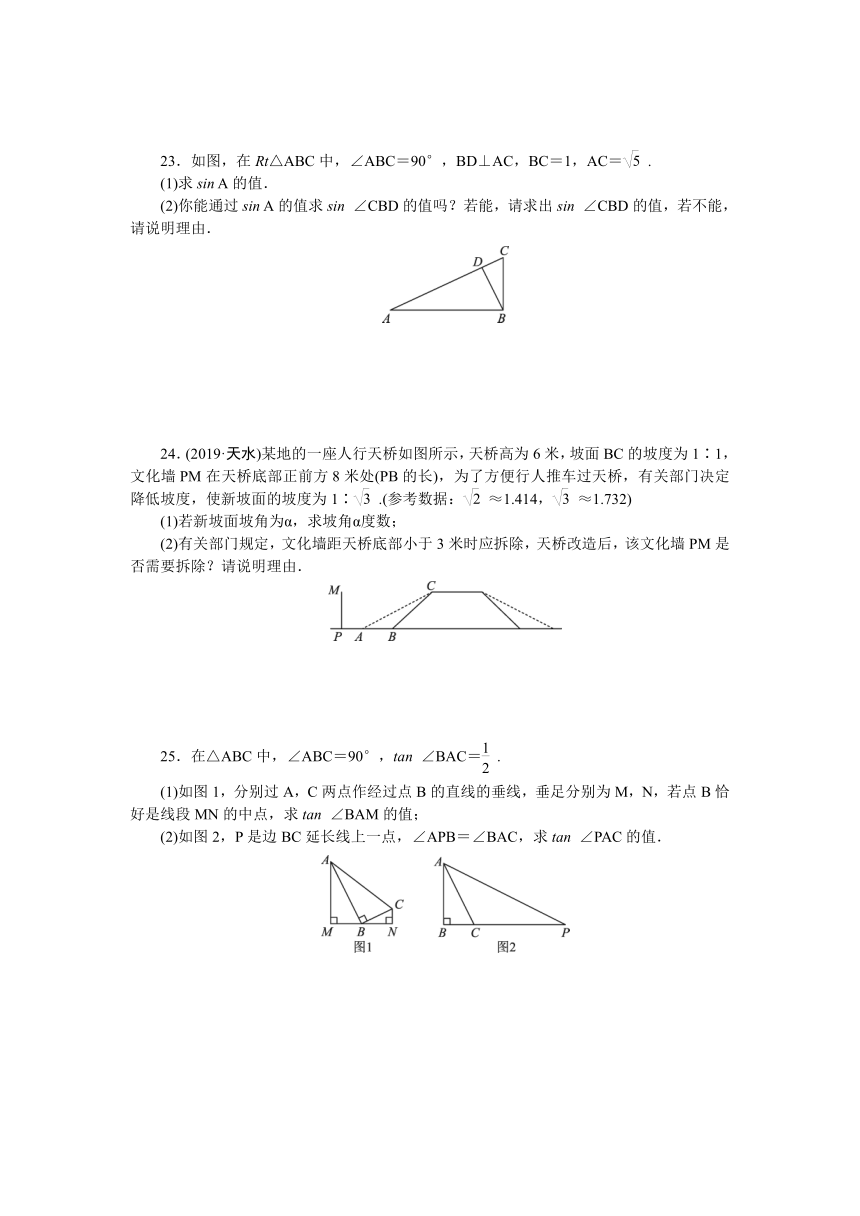
23.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC,BC=1,AC=.
(1)求sin
A的值.
(2)你能通过sin
A的值求sin
∠CBD的值吗?若能,请求出sin
∠CBD的值,若不能,请说明理由.
24.(2019·天水)某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1∶1,文化墙PM在天桥底部正前方8米处(PB的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1∶.(参考数据:≈1.414,≈1.732)
(1)若新坡面坡角为α,求坡角α度数;
(2)有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙PM是否需要拆除?请说明理由.
25.在△ABC中,∠ABC=90°,tan
∠BAC=.
(1)如图1,分别过A,C两点作经过点B的直线的垂线,垂足分别为M,N,若点B恰好是线段MN的中点,求tan
∠BAM的值;
(2)如图2,P是边BC延长线上一点,∠APB=∠BAC,求tan
∠PAC的值.
26.(2019·江西)图1是一台实物投影仪,图2是它的示意图,折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8
cm,CD=8
cm,AB=30
cm,BC=35
cm.(结果精确到0.1)
(1)如图2,∠ABC=70°,BC∥OE.
①填空:∠BAO=________°;
②求投影探头的端点D到桌面OE的距离;
(2)如图3,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6
cm时,求∠ABC的大小.(参考数据:sin70°≈0.94,cos20°≈0.94,sin36.8°≈0.60,cos53.2°≈0.60)
第4章 单元检测题(答案版)
(时间:100分钟 满分:120分)
一、选择题(本题共12小题,每题3分,共36分)
1.计算:sin60°·tan30°=(
B
)
A.1
B.
C.
D.2
2.在Rt△ABC中,∠C=90°,如果AC=4,BC=3,那么∠A的正切值为(
A
)
A.
B.
C.
D.
3.在△ABC中,∠C=90°,AC=4,cos
A=,那么AB的长是(
B
)
A.5
B.6
C.8
D.9
4.如图,为测量河两岸相对两电线杆A,B间的距离,在距A点16
m的C处(AC⊥AB),测得∠ACB=52°,则A,B之间的距离应为(
C
)
A.16sin52°
m
B.16cos52°
m
C.16tan52°
m
D.
m
eq
\o(\s\up7(),\s\do5(第4题图))
eq
\o(\s\up7(),\s\do5(第5题图))
eq
\o(\s\up7(),\s\do5(第6题图))
eq
\o(\s\up7(),\s\do5(第7题图))
5.如图,在△ABC中,∠C=90°,cos
A=,则sin
B=(
A
)
A.
B.
C.
D.
6.如图所示,△ABC在正方形网格中的位置如图示(A,B,C均在格点上),AD⊥BC于点D.下列四个选项中正确的是(
C
)
A.sin
α=cos
α
B.sin
α=tan
α
C.sin
β=cos
β
D.sin
β=tan
β
7.为了方便行人推车过某天桥,市政府在10
m高的天桥一侧修建了40
m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是(
A
)
A.
B.
C.
D.
8.若锐角三角函数tan55°=a,则a的范围是(
B
)
A.0<a<1
B.1<a<2
C.2<a<3
D.3<a<4
9.如果sin2α+cos230°=1,那么锐角α的度数是(A
)
A.30°
B.45°
C.60°
D.90°
10.(2019·杭州)如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于(
D
)
A.a
sin
x+b
sin
x
B.a
cos
x+b
cos
x
C.a
sin
x+b
cos
x
D.a
cos
x+b
sin
x
eq
\o(\s\up7(),\s\do5(第10题图))
eq
\o(\s\up7(),\s\do5(第11题图))
eq
\o(\s\up7(),\s\do5(第12题图))
11.如图所示,在△ABC中,∠C=90°,AB=8,CD是AB边上的中线,作CD的垂直平分线与CD交于点E,与BC交于点F.若CF=x,tan
A=y,则x与y之间满足(
A
)
A.+4=x2
B.-4=x2
C.-8=x2
D.+8=x2
12.(2019·长沙)如图,△ABC中,AB=AC=10,tan
A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是(
B
)
A.2
B.4
C.5
D.10
二、填空题(本大题共6小题,每小题3分,共18分)
13.计算:4cos60°=__2__.
14.(2019·怀化)已知∠α为锐角,且sin
α=,则∠α=__30°__.
15.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的余弦值是____.
eq
\o(\s\up7(),\s\do5(第15题图))
eq
\o(\s\up7(),\s\do5(第16题图))
eq
\o(\s\up7(),\s\do5(第17题图))
eq
\o(\s\up7(),\s\do5(第18题图))
16.(2019·醴陵期末)如图,有一斜坡AB,坡顶B离地面的高度BC为30
m,斜坡AB的坡度为1∶2,则此斜坡AB长为__30_m__.
17.如图,△ABC中,cos
B=,sin
C=,BC=7,则△ABC的面积是____.
18.如图,在△ABC中,AD平分∠CAB交BC于点E.若∠BDA=90°,E是AD中点,DE=2,AB=5,则AC的长为____.
三、解答题(本大题共8个小题,第19,20题每题6分,第21,22题每题8分,第23,24题每题9分,第25,26题每题10分,共66分.解答应写出必要的文字说明、证明过程或验算步骤)
19.计算:2cos60°+4sin60°·tan30°-6cos245°.
解:原式=2×+4××-6×()2=1+2-3=0
20.在Rt△ABC中,∠C=90°,a=,b=,解这个直角三角形.
解:在Rt△ABC中,∵a2+b2=c2,a=,b=,∴c==2,∵tan
A===,∴∠A=30°,∴∠B=90°-∠A=90°-30°=60°
21.在一个Rt△ABC中,∠C=90°,当∠A=30°时,∠A的对边与斜边的比都等于,是一个固定值;当∠A=45°时,∠A的对边与斜边的比都等于,也是一个固定值,这就引发我们产生这样一个疑问;当∠A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值?
探究:任意画Rt△ABC和Rt△A′B′C′,使得∠C=∠C′=90°,∠A=∠A′=a,那么与有什么关系,你能解释一下吗?
解:=,理由:∵∠C=∠C′=90°,∠A=∠A′=a,∴Rt△ABC∽Rt△A′B′C′,∴=
22.(2019·西藏)由我国完全自主设计,自主建造的首艘国产航母于2018年5月成功完成首次海上试验任务.如图,航母由西向东航行,到达B处时,测得小岛A在北偏东60°方向上,航行20海里到达C点,这时测得小岛A在北偏东30°方向上,小岛A周围10海里内有暗礁,如果航母不改变航线继续向东航行,有没有触礁危险?请说明理由.
解:如果航母不改变航线继续向东航行,没有触礁的危险,理由如下:过点A作AD⊥BC,垂足为D,根据题意可知∠ABC=30°,∠ACD=60°,∵∠ACD=∠ABC+∠BAC,∴∠BAC=30°=∠ABC,∴CB=CA=20,在Rt△ACD中,∠ADC=90°,∠ACD=60°,sin
∠ACD=,∴sin60°=,∴AD=20×sin60°=20×=10>10,∴航母不改变航线继续向东航行,没有触礁的危险
23.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC,BC=1,AC=.
(1)求sin
A的值.
(2)你能通过sin
A的值求sin
∠CBD的值吗?若能,请求出sin
∠CBD的值,若不能,请说明理由.
解:(1)在Rt△ABC中,sin
A===
(2)能.∵BD⊥AC,∴∠BDC=90°,∵∠CBD+∠C=90°,∠A+∠C=90°,∴∠A=∠CBD,∴sin
∠CBD=sin
A=
24.(2019·天水)某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1∶1,文化墙PM在天桥底部正前方8米处(PB的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1∶.(参考数据:≈1.414,≈1.732)
(1)若新坡面坡角为α,求坡角α度数;
(2)有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙PM是否需要拆除?请说明理由.
解:(1)∵新坡面坡角为α,新坡面的坡度为1∶,∴tan
α==,∴α=30° (2)该文化墙PM不需要拆除,理由:作CD⊥AB于点D,则CD=6米,∵新坡面的坡度为1∶,∴tan
∠CAD===,解得AD=6米,∵坡面BC的坡度为1∶1,CD=6米,∴BD=6米,∴AB=AD-BD=(6-6)米,又∵PB=8米,∴PA=PB-AB=8-(6-6)=14-6≈14-6×1.732=3.6米>3米,∴该文化墙PM不需要拆除
25.在△ABC中,∠ABC=90°,tan
∠BAC=.
(1)如图1,分别过A,C两点作经过点B的直线的垂线,垂足分别为M,N,若点B恰好是线段MN的中点,求tan
∠BAM的值;
(2)如图2,P是边BC延长线上一点,∠APB=∠BAC,求tan
∠PAC的值.
解:(1)∵AM⊥MN,CN⊥MN,∴∠M=∠N=90°,∴∠MAB+∠ABM=90°,∵∠ABC=90°,∴∠NBC+∠ABM=90°,∴∠MAB=∠NBC,∴△AMB∽△BNC,∴==tan
∠BAC=.∵点B是线段MN的中点,∴BM=BN,∴在Rt△AMB中,tan
∠BAM==
(2)如图2,过点C作CD⊥AC交AP于点D,过点D作DE⊥BP于点E.∵tan
∠BAC=,∠APB=∠BAC,∴tan
∠BAC==,tan
∠APB==.设BC=x,则AB=2x,BP=4x,则CP=BP-BC=4x-x=3x.同理(1)中,可得∠BAC=∠ECD,∴∠APB=∠ECD.∵DE⊥BP,∴CE=EP=CP=x.同理(1)中,可得△ABC∽△CED,∴===,∴在Rt△ACD中,tan
∠PAC==
26.(2019·江西)图1是一台实物投影仪,图2是它的示意图,折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8
cm,CD=8
cm,AB=30
cm,BC=35
cm.(结果精确到0.1)
(1)如图2,∠ABC=70°,BC∥OE.
①填空:∠BAO=________°;
②求投影探头的端点D到桌面OE的距离;
(2)如图3,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6
cm时,求∠ABC的大小.(参考数据:sin70°≈0.94,cos20°≈0.94,sin36.8°≈0.60,cos53.2°≈0.60)
解:(1)①过点A作AG∥BC,如图1,则∠BAG=∠ABC=70°,∵BC∥OE,∴AG∥OE,∴∠GAO=∠AOE=90°,∴∠BAO=90°+70°=160°,故答案为:160
②过点A作AF⊥BC于点F,如图2,则AF=AB·sin
∠ABF=30sin70°≈28.2(cm),∴投影探头的端点D到桌面OE的距离为:AF+OA-CD=28.2+6.8-8=27(cm)
(2)过点D作DH⊥OE于点H,过点B作BM⊥CD,与DC延长线相交于点M,过A作AF⊥BM于点F,如图3,则∠MBA=70°,AF=28.2
cm,DH=6
cm,BC=35
cm,CD=8
cm,∴CM=AF+AO-DH-CD=28.2+6.8-6-8=21(cm),∴sin
∠MBC===0.6,∴∠MBC=36.8°,∴∠ABC=∠ABM-∠MBC=33.2°
(时间:100分钟 满分:120分)
一、选择题(本题共12小题,每题3分,共36分)
1.计算:sin60°·tan30°=(
)
A.1
B.
C.
D.2
2.在Rt△ABC中,∠C=90°,如果AC=4,BC=3,那么∠A的正切值为(
)
A.
B.
C.
D.
3.在△ABC中,∠C=90°,AC=4,cos
A=,那么AB的长是(
)
A.5
B.6
C.8
D.9
4.如图,为测量河两岸相对两电线杆A,B间的距离,在距A点16
m的C处(AC⊥AB),测得∠ACB=52°,则A,B之间的距离应为(
)
A.16sin52°
m
B.16cos52°
m
C.16tan52°
m
D.
m
eq
\o(\s\up7(),\s\do5(第4题图))
eq
\o(\s\up7(),\s\do5(第5题图))
eq
\o(\s\up7(),\s\do5(第6题图))
eq
\o(\s\up7(),\s\do5(第7题图))
5.如图,在△ABC中,∠C=90°,cos
A=,则sin
B=(
)
A.
B.
C.
D.
6.如图所示,△ABC在正方形网格中的位置如图示(A,B,C均在格点上),AD⊥BC于点D.下列四个选项中正确的是(
)
A.sin
α=cos
α
B.sin
α=tan
α
C.sin
β=cos
β
D.sin
β=tan
β
7.为了方便行人推车过某天桥,市政府在10
m高的天桥一侧修建了40
m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是(
)
A.
B.
C.
D.
8.若锐角三角函数tan55°=a,则a的范围是(
)
A.0<a<1
B.1<a<2
C.2<a<3
D.3<a<4
9.如果sin2α+cos230°=1,那么锐角α的度数是(
)
A.30°
B.45°
C.60°
D.90°
10.(2019·杭州)如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于(
)
A.a
sin
x+b
sin
x
B.a
cos
x+b
cos
x
C.a
sin
x+b
cos
x
D.a
cos
x+b
sin
x
eq
\o(\s\up7(),\s\do5(第10题图))
eq
\o(\s\up7(),\s\do5(第11题图))
eq
\o(\s\up7(),\s\do5(第12题图))
11.如图所示,在△ABC中,∠C=90°,AB=8,CD是AB边上的中线,作CD的垂直平分线与CD交于点E,与BC交于点F.若CF=x,tan
A=y,则x与y之间满足(
)
A.+4=x2
B.-4=x2
C.-8=x2
D.+8=x2
12.(2019·长沙)如图,△ABC中,AB=AC=10,tan
A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是(
)
A.2
B.4
C.5
D.10
二、填空题(本大题共6小题,每小题3分,共18分)
13.计算:4cos60°=(
).
14.(2019·怀化)已知∠α为锐角,且sin
α=,则∠α=(
).
15.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的余弦值是(
).
eq
\o(\s\up7(),\s\do5(第15题图))
eq
\o(\s\up7(),\s\do5(第16题图))
eq
\o(\s\up7(),\s\do5(第17题图))
eq
\o(\s\up7(),\s\do5(第18题图))
16.(2019·醴陵期末)如图,有一斜坡AB,坡顶B离地面的高度BC为30
m,斜坡AB的坡度为1∶2,则此斜坡AB长为(
).
17.如图,△ABC中,cos
B=,sin
C=,BC=7,则△ABC的面积(
)
18.如图,在△ABC中,AD平分∠CAB交BC于点E.若∠BDA=90°,E是AD中点,DE=2,AB=5,则AC的长为(
).
三、解答题(本大题共8个小题,第19,20题每题6分,第21,22题每题8分,第23,24题每题9分,第25,26题每题10分,共66分.解答应写出必要的文字说明、证明过程或验算步骤)
19.计算:2cos60°+4sin60°·tan30°-6cos245°.
20.在Rt△ABC中,∠C=90°,a=,b=,解这个直角三角形.
21.在一个Rt△ABC中,∠C=90°,当∠A=30°时,∠A的对边与斜边的比都等于,是一个固定值;当∠A=45°时,∠A的对边与斜边的比都等于,也是一个固定值,这就引发我们产生这样一个疑问;当∠A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值?
探究:任意画Rt△ABC和Rt△A′B′C′,使得∠C=∠C′=90°,∠A=∠A′=a,那么与有什么关系,你能解释一下吗?
22.(2019·西藏)由我国完全自主设计,自主建造的首艘国产航母于2018年5月成功完成首次海上试验任务.如图,航母由西向东航行,到达B处时,测得小岛A在北偏东60°方向上,航行20海里到达C点,这时测得小岛A在北偏东30°方向上,小岛A周围10海里内有暗礁,如果航母不改变航线继续向东航行,有没有触礁危险?请说明理由.
23.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC,BC=1,AC=.
(1)求sin
A的值.
(2)你能通过sin
A的值求sin
∠CBD的值吗?若能,请求出sin
∠CBD的值,若不能,请说明理由.
24.(2019·天水)某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1∶1,文化墙PM在天桥底部正前方8米处(PB的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1∶.(参考数据:≈1.414,≈1.732)
(1)若新坡面坡角为α,求坡角α度数;
(2)有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙PM是否需要拆除?请说明理由.
25.在△ABC中,∠ABC=90°,tan
∠BAC=.
(1)如图1,分别过A,C两点作经过点B的直线的垂线,垂足分别为M,N,若点B恰好是线段MN的中点,求tan
∠BAM的值;
(2)如图2,P是边BC延长线上一点,∠APB=∠BAC,求tan
∠PAC的值.
26.(2019·江西)图1是一台实物投影仪,图2是它的示意图,折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8
cm,CD=8
cm,AB=30
cm,BC=35
cm.(结果精确到0.1)
(1)如图2,∠ABC=70°,BC∥OE.
①填空:∠BAO=________°;
②求投影探头的端点D到桌面OE的距离;
(2)如图3,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6
cm时,求∠ABC的大小.(参考数据:sin70°≈0.94,cos20°≈0.94,sin36.8°≈0.60,cos53.2°≈0.60)
第4章 单元检测题(答案版)
(时间:100分钟 满分:120分)
一、选择题(本题共12小题,每题3分,共36分)
1.计算:sin60°·tan30°=(
B
)
A.1
B.
C.
D.2
2.在Rt△ABC中,∠C=90°,如果AC=4,BC=3,那么∠A的正切值为(
A
)
A.
B.
C.
D.
3.在△ABC中,∠C=90°,AC=4,cos
A=,那么AB的长是(
B
)
A.5
B.6
C.8
D.9
4.如图,为测量河两岸相对两电线杆A,B间的距离,在距A点16
m的C处(AC⊥AB),测得∠ACB=52°,则A,B之间的距离应为(
C
)
A.16sin52°
m
B.16cos52°
m
C.16tan52°
m
D.
m
eq
\o(\s\up7(),\s\do5(第4题图))
eq
\o(\s\up7(),\s\do5(第5题图))
eq
\o(\s\up7(),\s\do5(第6题图))
eq
\o(\s\up7(),\s\do5(第7题图))
5.如图,在△ABC中,∠C=90°,cos
A=,则sin
B=(
A
)
A.
B.
C.
D.
6.如图所示,△ABC在正方形网格中的位置如图示(A,B,C均在格点上),AD⊥BC于点D.下列四个选项中正确的是(
C
)
A.sin
α=cos
α
B.sin
α=tan
α
C.sin
β=cos
β
D.sin
β=tan
β
7.为了方便行人推车过某天桥,市政府在10
m高的天桥一侧修建了40
m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是(
A
)
A.
B.
C.
D.
8.若锐角三角函数tan55°=a,则a的范围是(
B
)
A.0<a<1
B.1<a<2
C.2<a<3
D.3<a<4
9.如果sin2α+cos230°=1,那么锐角α的度数是(A
)
A.30°
B.45°
C.60°
D.90°
10.(2019·杭州)如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于(
D
)
A.a
sin
x+b
sin
x
B.a
cos
x+b
cos
x
C.a
sin
x+b
cos
x
D.a
cos
x+b
sin
x
eq
\o(\s\up7(),\s\do5(第10题图))
eq
\o(\s\up7(),\s\do5(第11题图))
eq
\o(\s\up7(),\s\do5(第12题图))
11.如图所示,在△ABC中,∠C=90°,AB=8,CD是AB边上的中线,作CD的垂直平分线与CD交于点E,与BC交于点F.若CF=x,tan
A=y,则x与y之间满足(
A
)
A.+4=x2
B.-4=x2
C.-8=x2
D.+8=x2
12.(2019·长沙)如图,△ABC中,AB=AC=10,tan
A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是(
B
)
A.2
B.4
C.5
D.10
二、填空题(本大题共6小题,每小题3分,共18分)
13.计算:4cos60°=__2__.
14.(2019·怀化)已知∠α为锐角,且sin
α=,则∠α=__30°__.
15.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的余弦值是____.
eq
\o(\s\up7(),\s\do5(第15题图))
eq
\o(\s\up7(),\s\do5(第16题图))
eq
\o(\s\up7(),\s\do5(第17题图))
eq
\o(\s\up7(),\s\do5(第18题图))
16.(2019·醴陵期末)如图,有一斜坡AB,坡顶B离地面的高度BC为30
m,斜坡AB的坡度为1∶2,则此斜坡AB长为__30_m__.
17.如图,△ABC中,cos
B=,sin
C=,BC=7,则△ABC的面积是____.
18.如图,在△ABC中,AD平分∠CAB交BC于点E.若∠BDA=90°,E是AD中点,DE=2,AB=5,则AC的长为____.
三、解答题(本大题共8个小题,第19,20题每题6分,第21,22题每题8分,第23,24题每题9分,第25,26题每题10分,共66分.解答应写出必要的文字说明、证明过程或验算步骤)
19.计算:2cos60°+4sin60°·tan30°-6cos245°.
解:原式=2×+4××-6×()2=1+2-3=0
20.在Rt△ABC中,∠C=90°,a=,b=,解这个直角三角形.
解:在Rt△ABC中,∵a2+b2=c2,a=,b=,∴c==2,∵tan
A===,∴∠A=30°,∴∠B=90°-∠A=90°-30°=60°
21.在一个Rt△ABC中,∠C=90°,当∠A=30°时,∠A的对边与斜边的比都等于,是一个固定值;当∠A=45°时,∠A的对边与斜边的比都等于,也是一个固定值,这就引发我们产生这样一个疑问;当∠A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值?
探究:任意画Rt△ABC和Rt△A′B′C′,使得∠C=∠C′=90°,∠A=∠A′=a,那么与有什么关系,你能解释一下吗?
解:=,理由:∵∠C=∠C′=90°,∠A=∠A′=a,∴Rt△ABC∽Rt△A′B′C′,∴=
22.(2019·西藏)由我国完全自主设计,自主建造的首艘国产航母于2018年5月成功完成首次海上试验任务.如图,航母由西向东航行,到达B处时,测得小岛A在北偏东60°方向上,航行20海里到达C点,这时测得小岛A在北偏东30°方向上,小岛A周围10海里内有暗礁,如果航母不改变航线继续向东航行,有没有触礁危险?请说明理由.
解:如果航母不改变航线继续向东航行,没有触礁的危险,理由如下:过点A作AD⊥BC,垂足为D,根据题意可知∠ABC=30°,∠ACD=60°,∵∠ACD=∠ABC+∠BAC,∴∠BAC=30°=∠ABC,∴CB=CA=20,在Rt△ACD中,∠ADC=90°,∠ACD=60°,sin
∠ACD=,∴sin60°=,∴AD=20×sin60°=20×=10>10,∴航母不改变航线继续向东航行,没有触礁的危险
23.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC,BC=1,AC=.
(1)求sin
A的值.
(2)你能通过sin
A的值求sin
∠CBD的值吗?若能,请求出sin
∠CBD的值,若不能,请说明理由.
解:(1)在Rt△ABC中,sin
A===
(2)能.∵BD⊥AC,∴∠BDC=90°,∵∠CBD+∠C=90°,∠A+∠C=90°,∴∠A=∠CBD,∴sin
∠CBD=sin
A=
24.(2019·天水)某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1∶1,文化墙PM在天桥底部正前方8米处(PB的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1∶.(参考数据:≈1.414,≈1.732)
(1)若新坡面坡角为α,求坡角α度数;
(2)有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙PM是否需要拆除?请说明理由.
解:(1)∵新坡面坡角为α,新坡面的坡度为1∶,∴tan
α==,∴α=30° (2)该文化墙PM不需要拆除,理由:作CD⊥AB于点D,则CD=6米,∵新坡面的坡度为1∶,∴tan
∠CAD===,解得AD=6米,∵坡面BC的坡度为1∶1,CD=6米,∴BD=6米,∴AB=AD-BD=(6-6)米,又∵PB=8米,∴PA=PB-AB=8-(6-6)=14-6≈14-6×1.732=3.6米>3米,∴该文化墙PM不需要拆除
25.在△ABC中,∠ABC=90°,tan
∠BAC=.
(1)如图1,分别过A,C两点作经过点B的直线的垂线,垂足分别为M,N,若点B恰好是线段MN的中点,求tan
∠BAM的值;
(2)如图2,P是边BC延长线上一点,∠APB=∠BAC,求tan
∠PAC的值.
解:(1)∵AM⊥MN,CN⊥MN,∴∠M=∠N=90°,∴∠MAB+∠ABM=90°,∵∠ABC=90°,∴∠NBC+∠ABM=90°,∴∠MAB=∠NBC,∴△AMB∽△BNC,∴==tan
∠BAC=.∵点B是线段MN的中点,∴BM=BN,∴在Rt△AMB中,tan
∠BAM==
(2)如图2,过点C作CD⊥AC交AP于点D,过点D作DE⊥BP于点E.∵tan
∠BAC=,∠APB=∠BAC,∴tan
∠BAC==,tan
∠APB==.设BC=x,则AB=2x,BP=4x,则CP=BP-BC=4x-x=3x.同理(1)中,可得∠BAC=∠ECD,∴∠APB=∠ECD.∵DE⊥BP,∴CE=EP=CP=x.同理(1)中,可得△ABC∽△CED,∴===,∴在Rt△ACD中,tan
∠PAC==
26.(2019·江西)图1是一台实物投影仪,图2是它的示意图,折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8
cm,CD=8
cm,AB=30
cm,BC=35
cm.(结果精确到0.1)
(1)如图2,∠ABC=70°,BC∥OE.
①填空:∠BAO=________°;
②求投影探头的端点D到桌面OE的距离;
(2)如图3,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6
cm时,求∠ABC的大小.(参考数据:sin70°≈0.94,cos20°≈0.94,sin36.8°≈0.60,cos53.2°≈0.60)
解:(1)①过点A作AG∥BC,如图1,则∠BAG=∠ABC=70°,∵BC∥OE,∴AG∥OE,∴∠GAO=∠AOE=90°,∴∠BAO=90°+70°=160°,故答案为:160
②过点A作AF⊥BC于点F,如图2,则AF=AB·sin
∠ABF=30sin70°≈28.2(cm),∴投影探头的端点D到桌面OE的距离为:AF+OA-CD=28.2+6.8-8=27(cm)
(2)过点D作DH⊥OE于点H,过点B作BM⊥CD,与DC延长线相交于点M,过A作AF⊥BM于点F,如图3,则∠MBA=70°,AF=28.2
cm,DH=6
cm,BC=35
cm,CD=8
cm,∴CM=AF+AO-DH-CD=28.2+6.8-6-8=21(cm),∴sin
∠MBC===0.6,∴∠MBC=36.8°,∴∠ABC=∠ABM-∠MBC=33.2°
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
