北师大版数学七年级上册3.2 代数式课件(第2课时 18张)
文档属性
| 名称 | 北师大版数学七年级上册3.2 代数式课件(第2课时 18张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 00:00:00 | ||
图片预览





文档简介
3.2 代数式(第2课时)
导入新知
某学校为了开展体育活动,要添置一批排球,每班配2个,学校另外留10个.如果这个学校共有n个班,总共需多少个排球?若这个学校有15个班(即n=15),则添置排球的总数为多少?若有20个班呢?
2n+10.当n=15时,代数式的值是40;
当n=20时,代数式的值是50.
?
素养目标
1.计算代数式的值的一般步骤.
2.求代数式的值应注意的问题.
3.用代数式求值推断反映的规律及意义.
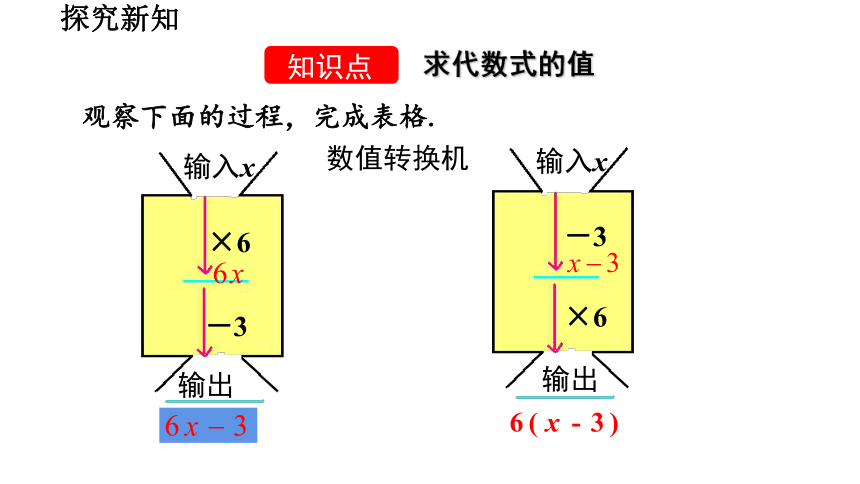
探究新知
知识点
求代数式的值
数值转换机
输入x
输入x
输出
输出
×6
-3
×6
-3
观察下面的过程,完成表格.
探究新知
输入
-2
-1/2
0
0.26
1/3
5/2
4.5
机器1的输出结果
机器2的输出结果
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
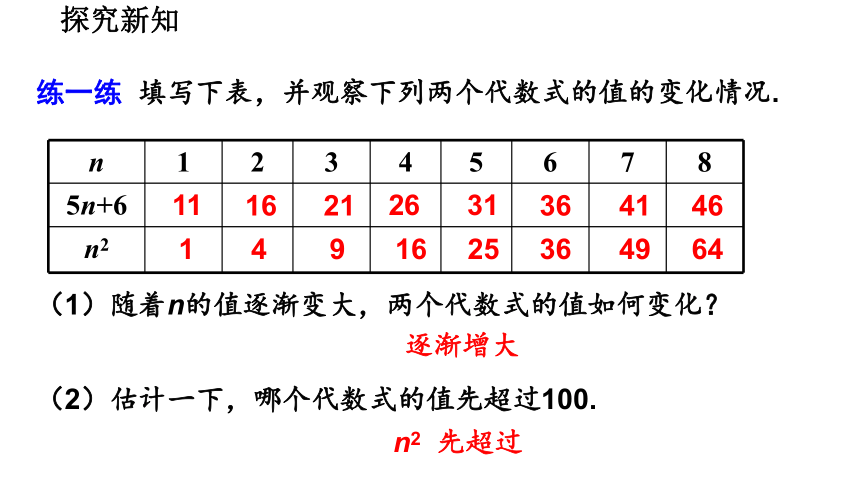
探究新知
练一练 填写下表,并观察下列两个代数式的值的变化情况.
n
1
2
3
4
5
6
7
8
5n+6
n2
11
16
21
26
31
36
41
46
1
4
9
16
25
36
49
64
(1)随着n的值逐渐变大,两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100.
逐渐增大
n2 先超过
探究新知
素养考点 1
求代数式的值
例
(1)当x=-3时,求 的值;
(2)当a=0.5,b=-2时,求 的值.
方法点拨:用数值代替代数式的字母,按照代数式中指明的运算,计算出的结果,叫做求代数式的值.求代数式的值,关键是正确代入数据,遇到负数时,要合理地添加括号.
解:(1)当x=-3时, ;
(2)当a=0.5,b=-2时,
巩固练习
变式训练
我们在计算不规则图形的面积时,有时采用“方格法”来计算.计算方法如下:假定每个小方格的边长为1个单位长,S为图形的面积,L是边界上的格点数,N是内部格点数,则有 . 请根据此方法计算图中四边形ABCD的面积.
巩固练习
解:由图可知边界上的格点数L=8,
内部格点数N =12,
所以四边形ABCD的面积为
连接中考
1.(2019·甘肃省中考真题)已知????+????= ,则代数式2a+2b-3的值是( )
?
A.2 B.-2 C.-4 D.?????
?
B
2.(2019·湖南省中考真题)当a=-1,b=3时,代数式2a-b的值等于_____.
-5
课堂检测
基础巩固题
1. 若a= ,b=2,c,d互为倒数,则代数式
2(a+b)-3cd的值为( )
A.2 B.-1 C.-3 D.0
D
课堂检测
基础巩固题
2.按如图所示的程序计算,若开始输入的数为x=3,则最后输出的结果是( )
A.6 B.21 C.156 D.231
D
课堂检测
基础巩固题
3.已知当x=1时,2ax2+bx的值为3,则当x=2时,ax2+bx的值为________.
6
4.已知 ,求 的值.
解: 因为 ,所以 .
所以原式= .
课堂检测
基础巩固题
5.当a=2,b=-1时,求下列代数式的值:
(1)2a+5b;
(2)a2-2ab+b2.
解:(1)当a=2,b=-1 时,
原式=22-2×2×(-1)+(-1)2=4+4+1=9.
原式=2×2+5×(-1)=4-5=-1.
(2)当a=2,b=-1时,
能力提升题
课堂检测
当a=3,b=2时,求代数式(a+b)(a2-ab+b2)与a3+b3的值,并根据计算结果写出你发现的结论.
②a3+b3
通过比较①②两式的计算结果,不难发现:
(a+b)(a2-ab+b2)=a3+b3
解:当a=3,b=2时,
① (a+b)(a2-ab+b2)
=35
=(3+2)(32-3×2+22)
=5×(9-6+4)
=5×7
=35.
=33+23
=27+8
拓广探索题
课堂检测
如图是某市设计的长方形休闲广场,两端是两个半圆形的花坛,中间是一个直径为长方形宽度一半的圆形喷水池.
(1)用图中所标字母表示广场空地(图中阴影部分)的面积;
(2)若休闲广场的长为80 m,宽为40 m,求广场空地的面积.
(计算结果保留π)
课堂检测
解:(1)广场空地的面积为xy-π(x2)????-π(x4)????=xy-516πx2.
?
(2)当x=40,y=80时,
xy-516πx2=40×80-516π×402=3 200-500π.
?
因此广场空地的面积为(3 200-500π)m2.
代数式求值
用数值代替代数式中的字母,按照代数式中指明的运算,计算出的结果,叫做求代数式的值.
求代数式的值,关键是正确代入数值,遇到负数时,要合理地添加括号.
课堂小结
导入新知
某学校为了开展体育活动,要添置一批排球,每班配2个,学校另外留10个.如果这个学校共有n个班,总共需多少个排球?若这个学校有15个班(即n=15),则添置排球的总数为多少?若有20个班呢?
2n+10.当n=15时,代数式的值是40;
当n=20时,代数式的值是50.
?
素养目标
1.计算代数式的值的一般步骤.
2.求代数式的值应注意的问题.
3.用代数式求值推断反映的规律及意义.
探究新知
知识点
求代数式的值
数值转换机
输入x
输入x
输出
输出
×6
-3
×6
-3
观察下面的过程,完成表格.
探究新知
输入
-2
-1/2
0
0.26
1/3
5/2
4.5
机器1的输出结果
机器2的输出结果
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
探究新知
练一练 填写下表,并观察下列两个代数式的值的变化情况.
n
1
2
3
4
5
6
7
8
5n+6
n2
11
16
21
26
31
36
41
46
1
4
9
16
25
36
49
64
(1)随着n的值逐渐变大,两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100.
逐渐增大
n2 先超过
探究新知
素养考点 1
求代数式的值
例
(1)当x=-3时,求 的值;
(2)当a=0.5,b=-2时,求 的值.
方法点拨:用数值代替代数式的字母,按照代数式中指明的运算,计算出的结果,叫做求代数式的值.求代数式的值,关键是正确代入数据,遇到负数时,要合理地添加括号.
解:(1)当x=-3时, ;
(2)当a=0.5,b=-2时,
巩固练习
变式训练
我们在计算不规则图形的面积时,有时采用“方格法”来计算.计算方法如下:假定每个小方格的边长为1个单位长,S为图形的面积,L是边界上的格点数,N是内部格点数,则有 . 请根据此方法计算图中四边形ABCD的面积.
巩固练习
解:由图可知边界上的格点数L=8,
内部格点数N =12,
所以四边形ABCD的面积为
连接中考
1.(2019·甘肃省中考真题)已知????+????= ,则代数式2a+2b-3的值是( )
?
A.2 B.-2 C.-4 D.?????
?
B
2.(2019·湖南省中考真题)当a=-1,b=3时,代数式2a-b的值等于_____.
-5
课堂检测
基础巩固题
1. 若a= ,b=2,c,d互为倒数,则代数式
2(a+b)-3cd的值为( )
A.2 B.-1 C.-3 D.0
D
课堂检测
基础巩固题
2.按如图所示的程序计算,若开始输入的数为x=3,则最后输出的结果是( )
A.6 B.21 C.156 D.231
D
课堂检测
基础巩固题
3.已知当x=1时,2ax2+bx的值为3,则当x=2时,ax2+bx的值为________.
6
4.已知 ,求 的值.
解: 因为 ,所以 .
所以原式= .
课堂检测
基础巩固题
5.当a=2,b=-1时,求下列代数式的值:
(1)2a+5b;
(2)a2-2ab+b2.
解:(1)当a=2,b=-1 时,
原式=22-2×2×(-1)+(-1)2=4+4+1=9.
原式=2×2+5×(-1)=4-5=-1.
(2)当a=2,b=-1时,
能力提升题
课堂检测
当a=3,b=2时,求代数式(a+b)(a2-ab+b2)与a3+b3的值,并根据计算结果写出你发现的结论.
②a3+b3
通过比较①②两式的计算结果,不难发现:
(a+b)(a2-ab+b2)=a3+b3
解:当a=3,b=2时,
① (a+b)(a2-ab+b2)
=35
=(3+2)(32-3×2+22)
=5×(9-6+4)
=5×7
=35.
=33+23
=27+8
拓广探索题
课堂检测
如图是某市设计的长方形休闲广场,两端是两个半圆形的花坛,中间是一个直径为长方形宽度一半的圆形喷水池.
(1)用图中所标字母表示广场空地(图中阴影部分)的面积;
(2)若休闲广场的长为80 m,宽为40 m,求广场空地的面积.
(计算结果保留π)
课堂检测
解:(1)广场空地的面积为xy-π(x2)????-π(x4)????=xy-516πx2.
?
(2)当x=40,y=80时,
xy-516πx2=40×80-516π×402=3 200-500π.
?
因此广场空地的面积为(3 200-500π)m2.
代数式求值
用数值代替代数式中的字母,按照代数式中指明的运算,计算出的结果,叫做求代数式的值.
求代数式的值,关键是正确代入数值,遇到负数时,要合理地添加括号.
课堂小结
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
