人教版九年级数学下册26.2实际问题与反比例函数习题(Word版 含答案)
文档属性
| 名称 | 人教版九年级数学下册26.2实际问题与反比例函数习题(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 334.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 19:43:01 | ||
图片预览


文档简介
实际问题与反比例函数
一、选择题(每小题5分,共25分)
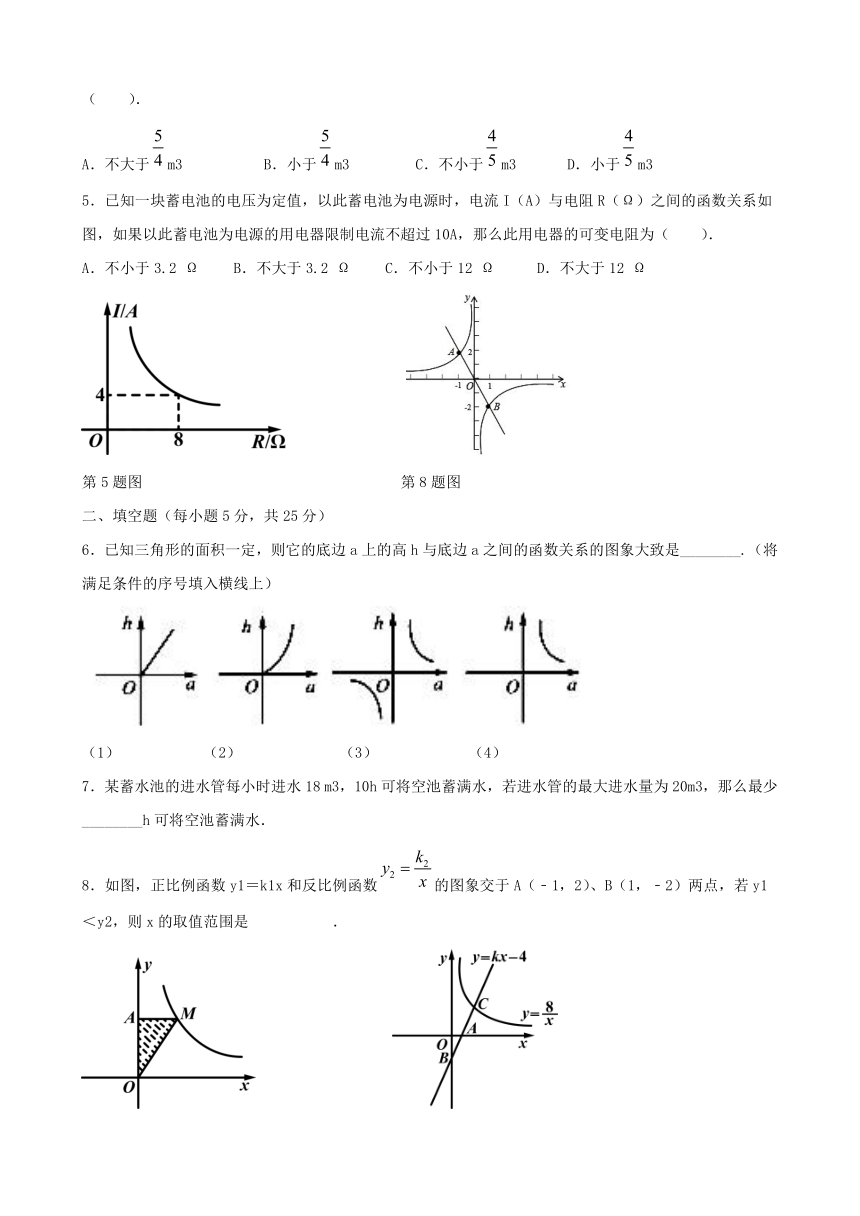
1.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线的一部分,则当x=16时,大棚内的温度约为(
).
A.18℃
B.15.5℃
C.13.5℃
D.12℃
2.如图,一次函数y1=k1x+b(k1,b为常数,且k1≠0)的图象与反比例函数(k2为常数,且k2≠0)的图象都经过点A(2,3),则当x>2时,y1与y2的大小关系为( ).
A.y1>y2
B.y1=y2
C.y1<y2
D.以上说法都不对
第1题图
第2题图
3.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图所示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( ).
A.
B.
C.
D.
第3题图
第4题图
4.某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将爆炸.为了安全,气球的体积应该( ).
A.不大于m3
B.小于m3
C.不小于m3
D.小于m3
5.已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,如果以此蓄电池为电源的用电器限制电流不超过10A,那么此用电器的可变电阻为( ).
A.不小于3.2
Ω
B.不大于3.2
Ω
C.不小于12
Ω
D.不大于12
Ω
第5题图
第8题图
二、填空题(每小题5分,共25分)
6.已知三角形的面积一定,则它的底边a上的高h与底边a之间的函数关系的图象大致是________.(将满足条件的序号填入横线上)
(1)
(2)
(3)
(4)
7.某蓄水池的进水管每小时进水18
m3,10h可将空池蓄满水,若进水管的最大进水量为20m3,那么最少________h可将空池蓄满水.
8.如图,正比例函数y1=k1x和反比例函数的图象交于A(﹣1,2)、B(1,﹣2)两点,若y1<y2,则x的取值范围是
.
第9题图
第10题图
9.如图,M为反比例函数的图象上的一点,MA垂直于y轴,垂足为A,△MAO的面积为2,则k的值为________.
10.如图,已知一次函数y=kx-4的图象与x轴、y轴分别交于A.B两点,与反比例函数在第一象限内的图象交于点C,且A为BC的中点,则k=________.
三、解答题(共50分)
11.(10分)某开发商准备开发建设一幢住宅区,工程需填土104米3,某工程队承包了该项填土任务.
(1)该工程队平均的填土量V(米3/天)与完成任务所需时间t(天)之间具有怎样的函数关系?
(2)该工程队共有10辆运输车,每辆车每天运土100米3,若工程必须在20天内完成任务,问:工程队每天至少派多少辆车运土,才能完成任务?
12.(10分)某工作人员打算利用不锈钢条制作一个面积为0.8m2的矩形模具.设矩形模具的长为y
m,宽为x
m.
(1)写出y与x之间的函数关系式,并说明y与x之间是什么函数关系;
(2)若使模具长比宽多1.6
m.已知每米这种不锈钢条的价格为6元,制作这个模具共需花多少钱?
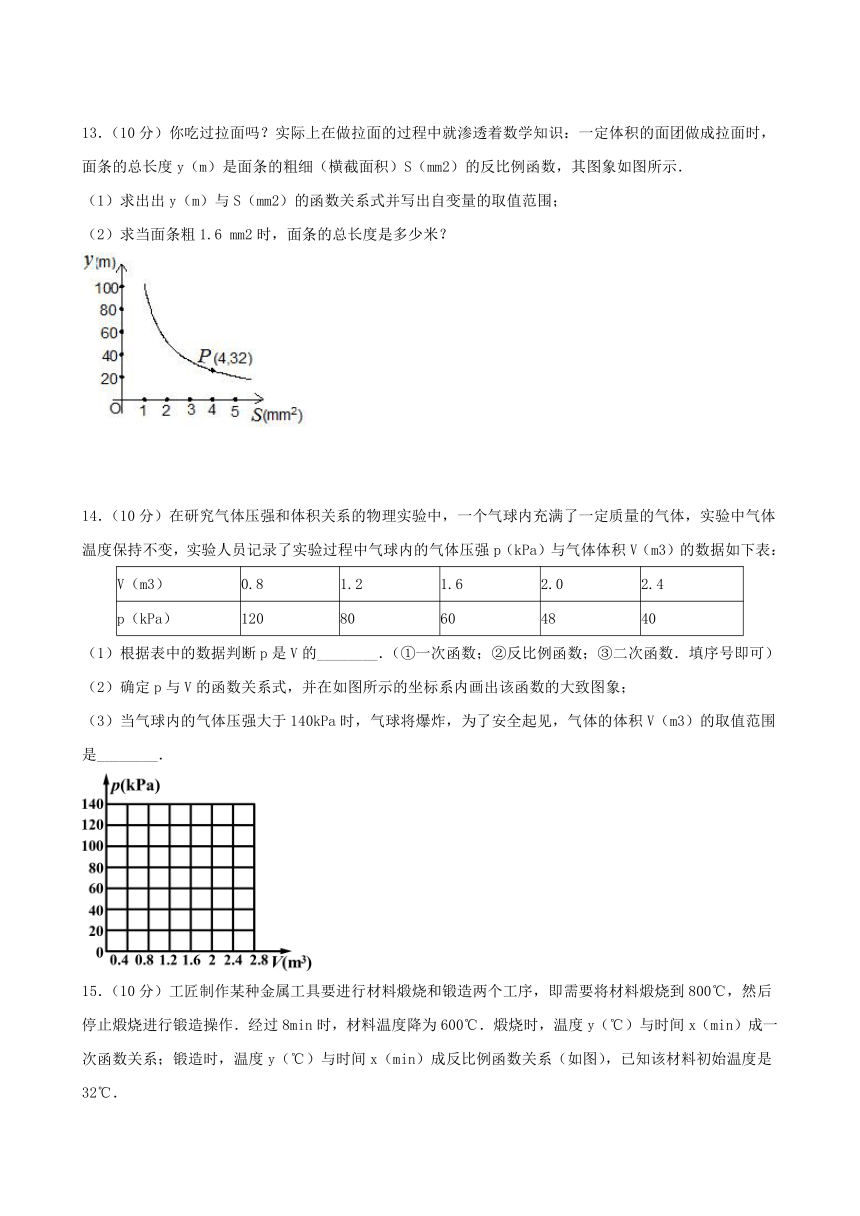
13.(10分)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面时,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示.
(1)求出出y(m)与S(mm2)的函数关系式并写出自变量的取值范围;
(2)求当面条粗1.6
mm2时,面条的总长度是多少米?
14.(10分)在研究气体压强和体积关系的物理实验中,一个气球内充满了一定质量的气体,实验中气体温度保持不变,实验人员记录了实验过程中气球内的气体压强p(kPa)与气体体积V(m3)的数据如下表:
V(m3)
0.8
1.2
1.6
2.0
2.4
p(kPa)
120
80
60
48
40
(1)根据表中的数据判断p是V的________.(①一次函数;②反比例函数;③二次函数.填序号即可)
(2)确定p与V的函数关系式,并在如图所示的坐标系内画出该函数的大致图象;
(3)当气球内的气体压强大于140kPa时,气球将爆炸,为了安全起见,气体的体积V(m3)的取值范围是________.
15.(10分)工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料煅烧到800℃,然后停止煅烧进行锻造操作.经过8min时,材料温度降为600℃.煅烧时,温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图),已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,那么锻造的操作时间有多长?
参考答案
1.C
【解析】根据题意求出反比例函数的解析式,然后将x=16代入解析式进行求解.根据题意可得反比例函数的解析式为y=,将x=16代入得:y=13.5.
2.A
【解析】∵题目中两个函数的图象都经过点A(2,3),
∴当x>2时,y1>y2,
故选A.
3.A
【解析】由题意知剪去的两个小矩形的面积都是10,即xy=10,所以y是x的反比例函数,根据自变量x的取值范围可以确定答案为A.
4.C
【解析】根据图象可得,当p=120时,V=0.8,再由图象可知随着气球体积的增大,气压逐渐减小,所以V不小于m3时,p不超过120kPa,故选C.
5.A
【解析】由题图知,(U≠0).
当R=8时,I=4,
∴U=IR=4×8=32.
∴
当0<I≤10时,.故选A.
6.(4)
【解析】先写出三角形底边a上的高h与底边a之间的函数关系h=,再根据反比例函数的图象特点及2s>0,h>0得出其图象只在第一象限.
故选(4).
7.9
【解析】∵蓄水池的最大蓄水量为18×10=180(m3),
∴180÷20=9(h).
8.或.
【解析】∵正比例函数和反比例函数的图象交于A(﹣1,2)、B(1,﹣2)两点,,∴此时x的取值范围是或,故答案为:或.
9.4
【解析】∵MA垂直于y轴,
∴,
∴,解得|k|=4.
由题图知k>0,
∴k=4.
10.4
【解析】把x=0代入y=kx-4,得y=-4,则B的坐标为(0,-4),
∵A为BC的中点,
∴C点的纵坐标为4,
把y=4代入,得x=2,
∴C点的坐标为(2,4),
把C(2,4)的坐标代入y=kx-4,得2k-4=4,解得k=4.
11.
【解析】(1)用“工作总量=工作效率×工作时间”作为等量关系先列等式,再将其转化为函数形式.
(2)根据“20天参加运土的所有车辆运土的总和不小于总工作量104米3”,列出不等式解题.
解:(1)由题意,得Vt=104,
∴
(2)设工程队每天派x辆车运土,才能完成任务,
则20×100x≥104,
解得x≥5.
答:工程队每天至少派5辆车运土,才能完成任务.
12.(1),y与x之间是反比例函数关系
(2)共需花28.8元
【解析】(1),y与x之间是反比例函数关系.
(2)∵模具长比宽多1.6m,∴
y=(x+1.6)m,把y=x+1.6代入,得,解得x1=0.4,x2=-2,经检验,x1=0.4,x2=-2都是的解,但x2=-2不合题意,故x=0.4,∴y=2,∴(2+0.4)×2×6=28.8(元).
答:制作这个模具共需花28.8元.
13.(1)();(2)80.
【解析】首先根据题意,y与s的关系为乘积一定,为面团的体积,故y与s的关系是反比例函数关系,将数据代入用待定系数法可得反比例函数的关系式;进一步求解可得答案.
解:(1)设y与s的函数关系式为,将s=4,y=32代入上式,解得:k=4×32=128,
∴();∴y与x的函数关系式();
(2)当时,,故当面条粗1.6mm2时,面条的总长度是80米.
14.(1)②.
(2).
图象如图所示:
(3)由图象及反比例函数的性质可知:当m3时,压强小于等于140kPa.
【解析】(1)②.
(2)设函数关系式为,把V=1.2,p=80代入,得m=1.2×80=96.∴p与V的关系式为.
图象如图所示:
(3)由图象及反比例函数的性质可知:当m3时,压强小于等于140kPa.
15.(1)锻造时的函数关系式为,自变量的取值范围是x≥6;
煅烧时的函数关系式为y=128x+32(0≤x≤6)
(2)锻造的操作时间有4分钟
【解析】(1)设锻造时的函数关系式为(k≠0),
则,
∴k=4800,
∴锻造时的函数关系式为.
当y=800时,,解得x=6,
∴点B的坐标为(6,800).
∴自变量的取值范围是x≥6.
设煅烧时的函数关系式为y=ax+b(a≠0),
则
解得
∴煅烧时的函数关系式为y=128x+32(0≤x≤6).
(2)y=480时,,10-6=4,
∴锻造的操作时间有4分钟.
一、选择题(每小题5分,共25分)
1.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线的一部分,则当x=16时,大棚内的温度约为(
).
A.18℃
B.15.5℃
C.13.5℃
D.12℃
2.如图,一次函数y1=k1x+b(k1,b为常数,且k1≠0)的图象与反比例函数(k2为常数,且k2≠0)的图象都经过点A(2,3),则当x>2时,y1与y2的大小关系为( ).
A.y1>y2
B.y1=y2
C.y1<y2
D.以上说法都不对
第1题图
第2题图
3.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图所示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( ).
A.
B.
C.
D.
第3题图
第4题图
4.某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将爆炸.为了安全,气球的体积应该( ).
A.不大于m3
B.小于m3
C.不小于m3
D.小于m3
5.已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,如果以此蓄电池为电源的用电器限制电流不超过10A,那么此用电器的可变电阻为( ).
A.不小于3.2
Ω
B.不大于3.2
Ω
C.不小于12
Ω
D.不大于12
Ω
第5题图
第8题图
二、填空题(每小题5分,共25分)
6.已知三角形的面积一定,则它的底边a上的高h与底边a之间的函数关系的图象大致是________.(将满足条件的序号填入横线上)
(1)
(2)
(3)
(4)
7.某蓄水池的进水管每小时进水18
m3,10h可将空池蓄满水,若进水管的最大进水量为20m3,那么最少________h可将空池蓄满水.
8.如图,正比例函数y1=k1x和反比例函数的图象交于A(﹣1,2)、B(1,﹣2)两点,若y1<y2,则x的取值范围是
.
第9题图
第10题图
9.如图,M为反比例函数的图象上的一点,MA垂直于y轴,垂足为A,△MAO的面积为2,则k的值为________.
10.如图,已知一次函数y=kx-4的图象与x轴、y轴分别交于A.B两点,与反比例函数在第一象限内的图象交于点C,且A为BC的中点,则k=________.
三、解答题(共50分)
11.(10分)某开发商准备开发建设一幢住宅区,工程需填土104米3,某工程队承包了该项填土任务.
(1)该工程队平均的填土量V(米3/天)与完成任务所需时间t(天)之间具有怎样的函数关系?
(2)该工程队共有10辆运输车,每辆车每天运土100米3,若工程必须在20天内完成任务,问:工程队每天至少派多少辆车运土,才能完成任务?
12.(10分)某工作人员打算利用不锈钢条制作一个面积为0.8m2的矩形模具.设矩形模具的长为y
m,宽为x
m.
(1)写出y与x之间的函数关系式,并说明y与x之间是什么函数关系;
(2)若使模具长比宽多1.6
m.已知每米这种不锈钢条的价格为6元,制作这个模具共需花多少钱?
13.(10分)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面时,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示.
(1)求出出y(m)与S(mm2)的函数关系式并写出自变量的取值范围;
(2)求当面条粗1.6
mm2时,面条的总长度是多少米?
14.(10分)在研究气体压强和体积关系的物理实验中,一个气球内充满了一定质量的气体,实验中气体温度保持不变,实验人员记录了实验过程中气球内的气体压强p(kPa)与气体体积V(m3)的数据如下表:
V(m3)
0.8
1.2
1.6
2.0
2.4
p(kPa)
120
80
60
48
40
(1)根据表中的数据判断p是V的________.(①一次函数;②反比例函数;③二次函数.填序号即可)
(2)确定p与V的函数关系式,并在如图所示的坐标系内画出该函数的大致图象;
(3)当气球内的气体压强大于140kPa时,气球将爆炸,为了安全起见,气体的体积V(m3)的取值范围是________.
15.(10分)工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料煅烧到800℃,然后停止煅烧进行锻造操作.经过8min时,材料温度降为600℃.煅烧时,温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图),已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,那么锻造的操作时间有多长?
参考答案
1.C
【解析】根据题意求出反比例函数的解析式,然后将x=16代入解析式进行求解.根据题意可得反比例函数的解析式为y=,将x=16代入得:y=13.5.
2.A
【解析】∵题目中两个函数的图象都经过点A(2,3),
∴当x>2时,y1>y2,
故选A.
3.A
【解析】由题意知剪去的两个小矩形的面积都是10,即xy=10,所以y是x的反比例函数,根据自变量x的取值范围可以确定答案为A.
4.C
【解析】根据图象可得,当p=120时,V=0.8,再由图象可知随着气球体积的增大,气压逐渐减小,所以V不小于m3时,p不超过120kPa,故选C.
5.A
【解析】由题图知,(U≠0).
当R=8时,I=4,
∴U=IR=4×8=32.
∴
当0<I≤10时,.故选A.
6.(4)
【解析】先写出三角形底边a上的高h与底边a之间的函数关系h=,再根据反比例函数的图象特点及2s>0,h>0得出其图象只在第一象限.
故选(4).
7.9
【解析】∵蓄水池的最大蓄水量为18×10=180(m3),
∴180÷20=9(h).
8.或.
【解析】∵正比例函数和反比例函数的图象交于A(﹣1,2)、B(1,﹣2)两点,,∴此时x的取值范围是或,故答案为:或.
9.4
【解析】∵MA垂直于y轴,
∴,
∴,解得|k|=4.
由题图知k>0,
∴k=4.
10.4
【解析】把x=0代入y=kx-4,得y=-4,则B的坐标为(0,-4),
∵A为BC的中点,
∴C点的纵坐标为4,
把y=4代入,得x=2,
∴C点的坐标为(2,4),
把C(2,4)的坐标代入y=kx-4,得2k-4=4,解得k=4.
11.
【解析】(1)用“工作总量=工作效率×工作时间”作为等量关系先列等式,再将其转化为函数形式.
(2)根据“20天参加运土的所有车辆运土的总和不小于总工作量104米3”,列出不等式解题.
解:(1)由题意,得Vt=104,
∴
(2)设工程队每天派x辆车运土,才能完成任务,
则20×100x≥104,
解得x≥5.
答:工程队每天至少派5辆车运土,才能完成任务.
12.(1),y与x之间是反比例函数关系
(2)共需花28.8元
【解析】(1),y与x之间是反比例函数关系.
(2)∵模具长比宽多1.6m,∴
y=(x+1.6)m,把y=x+1.6代入,得,解得x1=0.4,x2=-2,经检验,x1=0.4,x2=-2都是的解,但x2=-2不合题意,故x=0.4,∴y=2,∴(2+0.4)×2×6=28.8(元).
答:制作这个模具共需花28.8元.
13.(1)();(2)80.
【解析】首先根据题意,y与s的关系为乘积一定,为面团的体积,故y与s的关系是反比例函数关系,将数据代入用待定系数法可得反比例函数的关系式;进一步求解可得答案.
解:(1)设y与s的函数关系式为,将s=4,y=32代入上式,解得:k=4×32=128,
∴();∴y与x的函数关系式();
(2)当时,,故当面条粗1.6mm2时,面条的总长度是80米.
14.(1)②.
(2).
图象如图所示:
(3)由图象及反比例函数的性质可知:当m3时,压强小于等于140kPa.
【解析】(1)②.
(2)设函数关系式为,把V=1.2,p=80代入,得m=1.2×80=96.∴p与V的关系式为.
图象如图所示:
(3)由图象及反比例函数的性质可知:当m3时,压强小于等于140kPa.
15.(1)锻造时的函数关系式为,自变量的取值范围是x≥6;
煅烧时的函数关系式为y=128x+32(0≤x≤6)
(2)锻造的操作时间有4分钟
【解析】(1)设锻造时的函数关系式为(k≠0),
则,
∴k=4800,
∴锻造时的函数关系式为.
当y=800时,,解得x=6,
∴点B的坐标为(6,800).
∴自变量的取值范围是x≥6.
设煅烧时的函数关系式为y=ax+b(a≠0),
则
解得
∴煅烧时的函数关系式为y=128x+32(0≤x≤6).
(2)y=480时,,10-6=4,
∴锻造的操作时间有4分钟.
