人教版八年级数学上册 12.2 三角形全等的判定 同步练习(Word版 无答案)
文档属性
| 名称 | 人教版八年级数学上册 12.2 三角形全等的判定 同步练习(Word版 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 153.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 10:24:42 | ||
图片预览

文档简介
八年级数学上册
12.2
三角形全等的判定
同步练习
题号
一
二
三
总分
得分
一、选择题(本大题共8小题,共24分)
AD是的中线,下列说法:;和面积相等;;≌其中正确的有.
A.
1个
B.
2个
C.
3个
D.
4个
如图,点P、Q分别是边长为4cm的等边边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为,下面四个结论正确的有个.
;≌;的度数不变,始终等于;当第秒或第秒时,为直角三角形.
A.
1
B.
2
C.
3
D.
4
用两个全等三角形拼成一个四边形.如果该四边形是正方形,那么这两个三角形一定是
A.
等腰三角形
B.
直角三角形
C.
等腰直角三角形
D.
等边三角形
如图,在中,D、E分别是AC、AB上的点,在≌≌,则的度数是
A.
B.
C.
D.
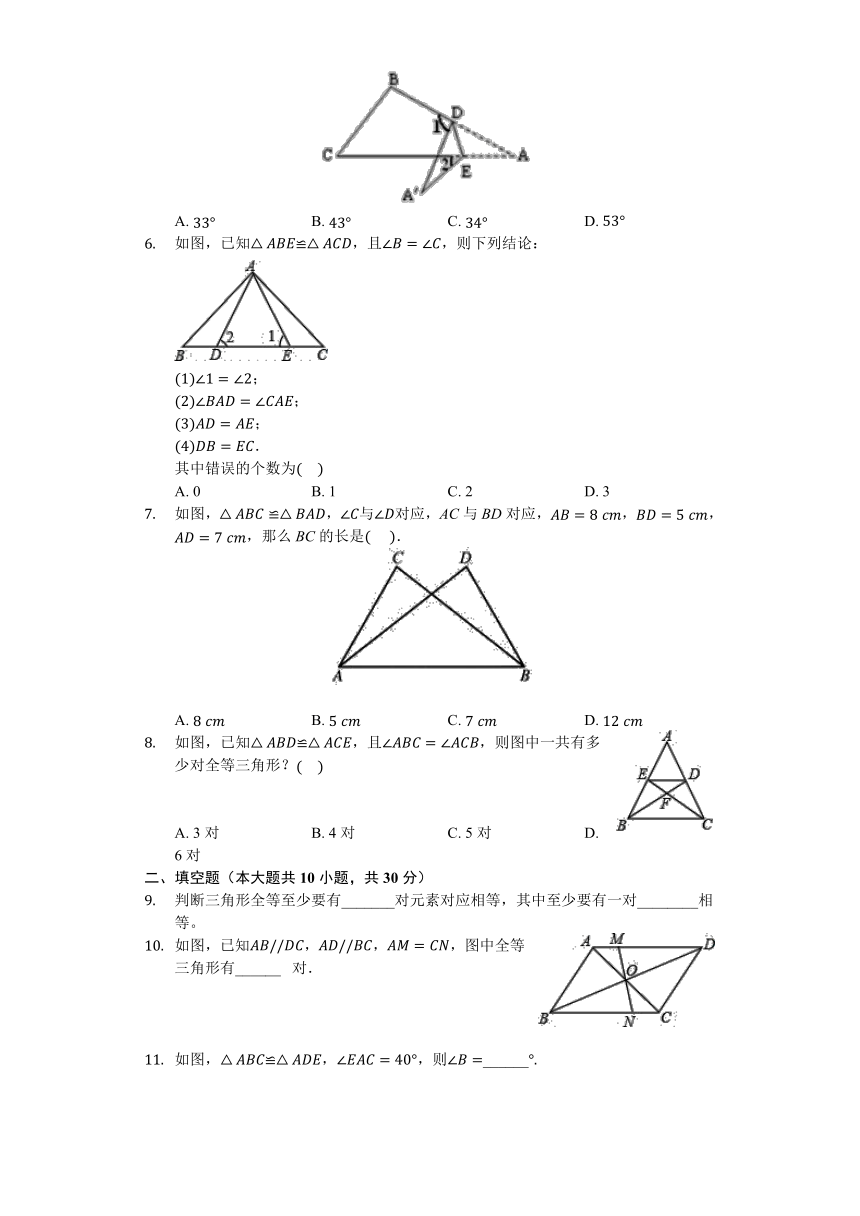
如图,把纸片沿DE折叠,当点A落在四边形BCED的外部时,,则的度数等于
A.
B.
C.
D.
如图,已知≌,且,则下列结论:
;
;
;
.
其中错误的个数为
??
A.
0
B.
1
C.
2
D.
3
如图,,与对应,AC与BD对应,,,,那么BC的长是???
.
A.
B.
C.
D.
如图,已知≌,且,则图中一共有多少对全等三角形?
A.
3对
B.
4对
C.
5对
D.
6对
二、填空题(本大题共10小题,共30分)
判断三角形全等至少要有_______对元素对应相等,其中至少要有一对________相等。
如图,已知,,,图中全等三角形有______
?对.
如图,≌,,则______
已知≌,若,则______.
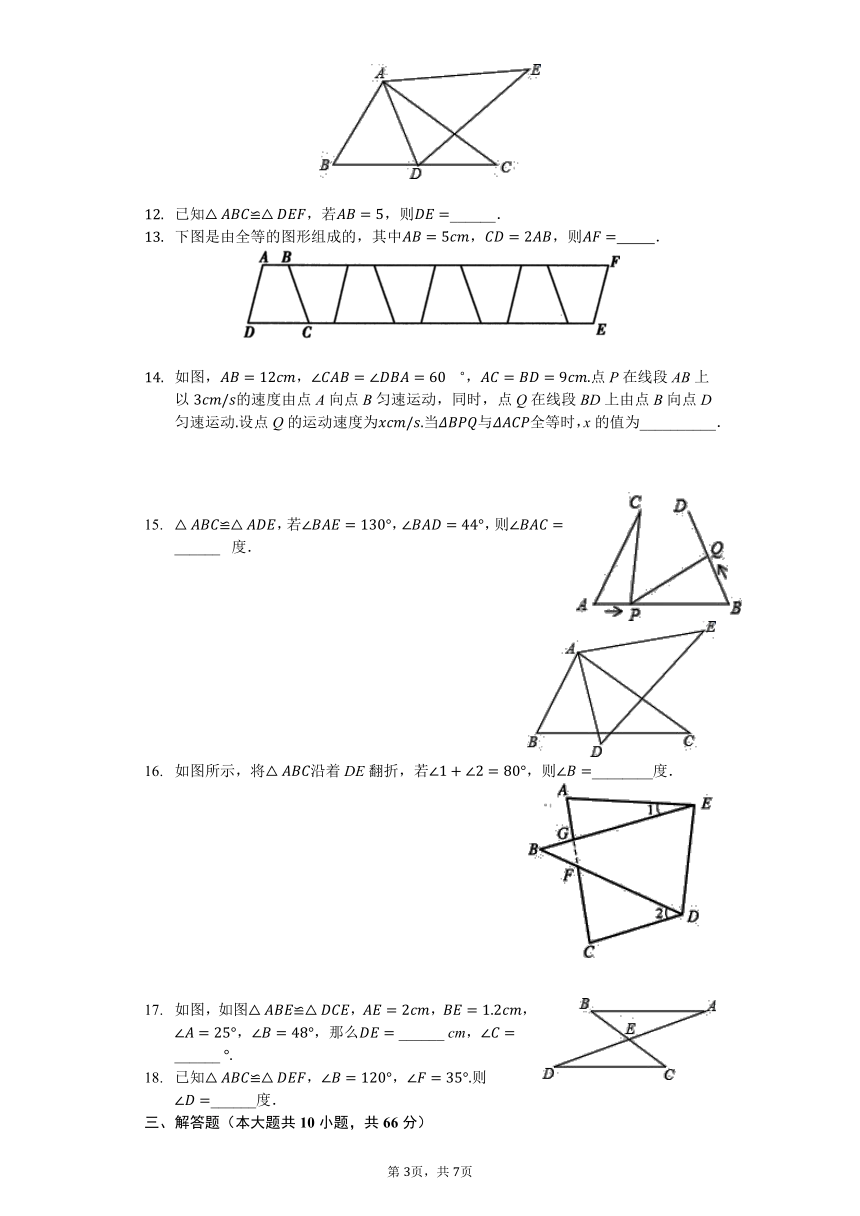
下图是由全等的图形组成的,其中,,则??????????.
如图,,,点P在线段AB上以的速度由点A向点B匀速运动,同时,点Q在线段BD上由点B向点D匀速运动设点Q的运动速度为当与全等时,x的值为__________.
≌,若,,则
______
?度.
如图所示,将沿着DE翻折,若,则________度.
如图,如图≌,,,,,那么
______
cm,
______
已知≌,,则______度.
三、解答题(本大题共10小题,共66分)
如图,≌,其中点A、B、C、D在一条直线上
若,,求的大小;
若,,求AB的长.
如图,D、E分别是的边AC、AB上的点.连接BD、CE.
若≌,试写出它们的对应边和对应角;
若≌,且,,求的度数.
如图,,点E、F在线段AC上,且试说明FD与BE的数量关系,并说明理由.
以锐角的边AC、AB为边向外作正方形ACDE和正方形ABGF,连结BE、CF.
试探索BE和CF的数量关系?并说明理由;
找出图中可以通过旋转而相互得到两个图形,并说出旋转过程.
用三角形和六边形按如图所示的规律拼图案.
第4个图案中,三角形有____个,六边形有____个;
第为正整数个图案中,三角形与六边形各有多少个?
第2017个图案中,三角形与六边形各有多少个?
是否存在某个符合上述规律的图案,其中有100个三角形与30个六边形?如果有,指出是第几个图案;如果没有,说明理由.
如图,已知≌,与是对应角.
写出边FG的对应边与的对应角.
若,,,求MN和HG的长.
如图,点B,M,N,C在同一直线上,且≌,,,求的度数.
如图,将绕点B顺时针旋转后得到点A对应点为,线段AC交线段DE于点F,求的度数.
如图,是等边三角形,AD为中线,,E在AC上,求的度数.
我们已经学习了角平分线的概念,那么你会用它解决有关问题吗?
如图所示,将长方形笔记本活页纸片的一角折过去,使角的顶点A落在处,BC为折痕.若,求的度数:
在条件下,如果将它的另一个角也斜折过去,并使CD边与重合,折痕为CE,如图所示,求和的度数;
如果在图中改变的大小,则的位置也随之改变,那么中的大小会不会改变?请说明理由.
第7页,共7页
12.2
三角形全等的判定
同步练习
题号
一
二
三
总分
得分
一、选择题(本大题共8小题,共24分)
AD是的中线,下列说法:;和面积相等;;≌其中正确的有.
A.
1个
B.
2个
C.
3个
D.
4个
如图,点P、Q分别是边长为4cm的等边边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为,下面四个结论正确的有个.
;≌;的度数不变,始终等于;当第秒或第秒时,为直角三角形.
A.
1
B.
2
C.
3
D.
4
用两个全等三角形拼成一个四边形.如果该四边形是正方形,那么这两个三角形一定是
A.
等腰三角形
B.
直角三角形
C.
等腰直角三角形
D.
等边三角形
如图,在中,D、E分别是AC、AB上的点,在≌≌,则的度数是
A.
B.
C.
D.
如图,把纸片沿DE折叠,当点A落在四边形BCED的外部时,,则的度数等于
A.
B.
C.
D.
如图,已知≌,且,则下列结论:
;
;
;
.
其中错误的个数为
??
A.
0
B.
1
C.
2
D.
3
如图,,与对应,AC与BD对应,,,,那么BC的长是???
.
A.
B.
C.
D.
如图,已知≌,且,则图中一共有多少对全等三角形?
A.
3对
B.
4对
C.
5对
D.
6对
二、填空题(本大题共10小题,共30分)
判断三角形全等至少要有_______对元素对应相等,其中至少要有一对________相等。
如图,已知,,,图中全等三角形有______
?对.
如图,≌,,则______
已知≌,若,则______.
下图是由全等的图形组成的,其中,,则??????????.
如图,,,点P在线段AB上以的速度由点A向点B匀速运动,同时,点Q在线段BD上由点B向点D匀速运动设点Q的运动速度为当与全等时,x的值为__________.
≌,若,,则
______
?度.
如图所示,将沿着DE翻折,若,则________度.
如图,如图≌,,,,,那么
______
cm,
______
已知≌,,则______度.
三、解答题(本大题共10小题,共66分)
如图,≌,其中点A、B、C、D在一条直线上
若,,求的大小;
若,,求AB的长.
如图,D、E分别是的边AC、AB上的点.连接BD、CE.
若≌,试写出它们的对应边和对应角;
若≌,且,,求的度数.
如图,,点E、F在线段AC上,且试说明FD与BE的数量关系,并说明理由.
以锐角的边AC、AB为边向外作正方形ACDE和正方形ABGF,连结BE、CF.
试探索BE和CF的数量关系?并说明理由;
找出图中可以通过旋转而相互得到两个图形,并说出旋转过程.
用三角形和六边形按如图所示的规律拼图案.
第4个图案中,三角形有____个,六边形有____个;
第为正整数个图案中,三角形与六边形各有多少个?
第2017个图案中,三角形与六边形各有多少个?
是否存在某个符合上述规律的图案,其中有100个三角形与30个六边形?如果有,指出是第几个图案;如果没有,说明理由.
如图,已知≌,与是对应角.
写出边FG的对应边与的对应角.
若,,,求MN和HG的长.
如图,点B,M,N,C在同一直线上,且≌,,,求的度数.
如图,将绕点B顺时针旋转后得到点A对应点为,线段AC交线段DE于点F,求的度数.
如图,是等边三角形,AD为中线,,E在AC上,求的度数.
我们已经学习了角平分线的概念,那么你会用它解决有关问题吗?
如图所示,将长方形笔记本活页纸片的一角折过去,使角的顶点A落在处,BC为折痕.若,求的度数:
在条件下,如果将它的另一个角也斜折过去,并使CD边与重合,折痕为CE,如图所示,求和的度数;
如果在图中改变的大小,则的位置也随之改变,那么中的大小会不会改变?请说明理由.
第7页,共7页
