人教版数学八年级上册 11.1.2 三角形的高、中线与角平分线 教案
文档属性
| 名称 | 人教版数学八年级上册 11.1.2 三角形的高、中线与角平分线 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 458.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 00:00:00 | ||
图片预览



文档简介
第八.二讲--三角形的高、中线与角平分线
初中数学
年级
八年级
重难点
重点:
1.了解三角形的高、中线与角平分线的概念,
会用工具准确画出三角形的高、中线与角平分线.
2.了解三角形的三条高、三条中线与三条角平分线分别交于一点.
难点:
1.三角形平分线与角平分线的区别,三角形的高与垂线的区别.
2.钝角三角形高的画法.
3.不同的三角形三条高的位置关系.
【知识储备】
三角形的
重要线段意义图形表示法三角形
的高线从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段1.AD是△ABC的BC上的高线.
2.AD⊥BC于D.
3.∠ADB=∠ADC=90°.三角形
的中线三角形中,连结一个顶点和它对边中点的
线段1.AD是△ABC的BC上的中线.
2.BD=DC=BC.三角形的
角平分线三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段1.AD是△ABC的∠BAC的平分线.
2.∠1=∠2=∠BAC.
【结论一】:每个三角形都能画出三条高。
【结论一】:每个三角形都能画出三条高。
相同点:三角形的三条高交于同一点。
不同点:锐角三角形的三条高交于三角形内一点,直角三角形的三条高交于直角的顶点,钝角三角形的三条高交于三角形外一点。
【结论二】:无论哪种三角形,它们都有三条中线,并且这三条中线都交于一点,这一点都在三角形内部。三角形的中线将三角形的面积平均分成两份。三角形三条中线相交于一点,这个交点叫做三角形的重心。
【结论三】:无论哪种三角形,它们都有三条角平分线,并且这三条角平分线都交于一点,这一点都在三角形内部。
(1)什么叫三角形的高?三角形的高与垂线有何区别和联系?
三角形的高是从三角形的一个顶点向它对边所在的直线作垂线,顶点和垂足之间的线段,而从三角形一个顶点向它对边所在的直线作垂线这条垂线是直线.
(2)什么叫三角形的中线?连结两点的线段与过两点的直线有何区别和联系?
三角形的中线是连结一个顶点和它对边的中点的线段,
而过两点的直线有着本质的不同,一个代表的是线段,另一个却是直线.
(3)什么叫三角形的角平分线?三角形的角平分线与角平分线有何区别和联系?
三角形的角平分线是三角形的一个内角平分线与它的对边相交,
这个角顶点与交点之间的线段,而角平分线指的是一条射线.
三角形的高、中线和角平分线是代表线段还是代表射线或直线?
三角形的高、中线和角平分线都代表线段,
这些线段的一个端点是三角形的一个顶点,另一个端点在这个顶点的对边上.
【典例精析】
典例1
已知:钝角△ABC,请画出△ABC的角平分线BD,AB边上的中线和AC边上的高,并用字母表示.
典例2
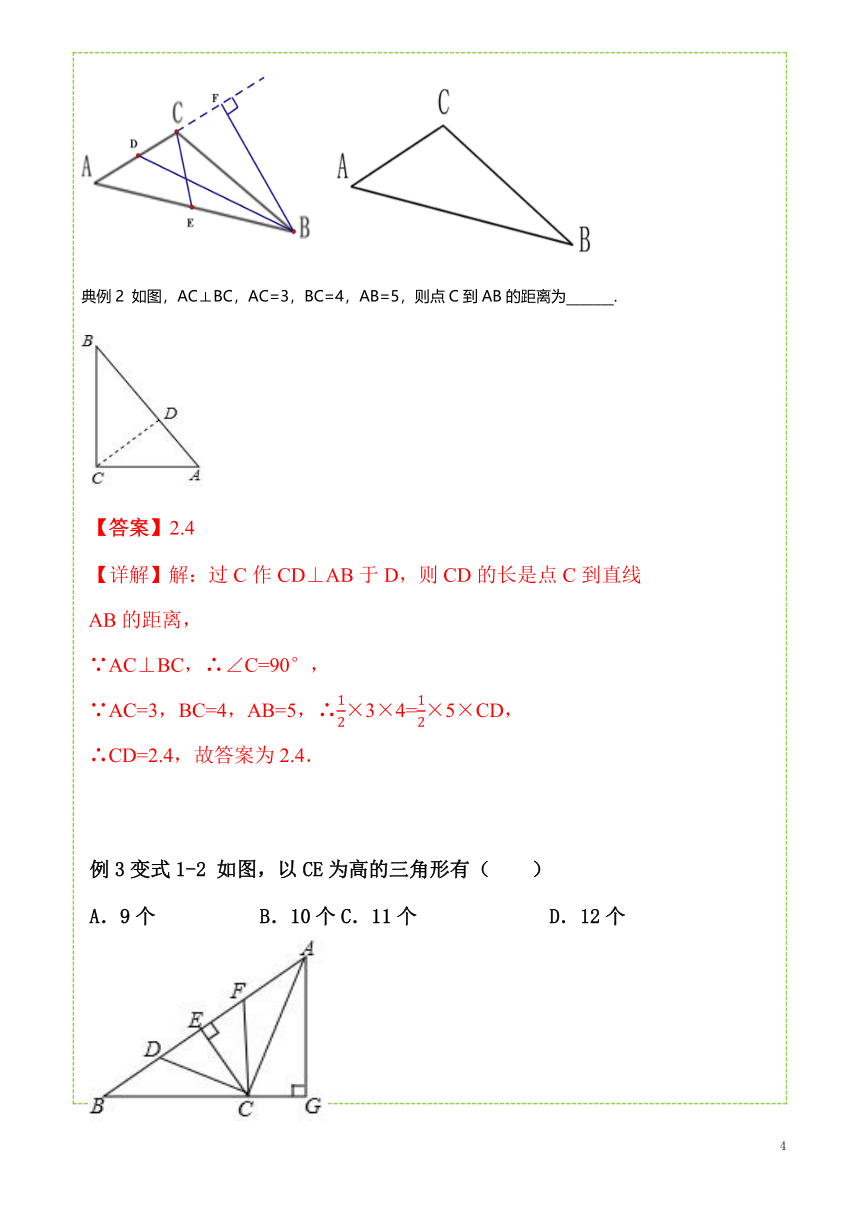
如图,AC⊥BC,AC=3,BC=4,AB=5,则点C到AB的距离为_______.
【答案】B
【详解】解:以CE为高的三角形就是以C为一个顶点,再从B,F,E,D,A中任意选两个点组成,
∴4+3+2+1=10(个).
∴以CE为高的三角形有10个.
故选:B.
典例4
如图,三角形ABC中,D为BC上的一点,且S△ABD=S△ADC,则AD为(
)
A.高
B.角平分线
C.中线
D.不能确定
典例5.
如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
解:∵AD是BC边上的高,∠EAD=5°,∴∠AED=85°,∵∠B=50°,
∴∠BAE=∠AED﹣∠B=85°﹣50°=35°,∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=70°,∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°.
典例6.如图,为△ABC的中线,为的中线.
(1),,求的度数;
(2)若△ABC的面积为20,,求△BDE中边上的高.
解:(1)在中,
,,
;
(2)过点作边上的高,
为的中线,为的中线,
,
,
,
的面积为20,,
,
即:
,
;
典例7如图BO、CO分别平分和,DE过点D且,,,求的周长.
解∵BO、CO分别平分和,
,,
又.
,,
,,
,,
∴△ADE周长
【当堂小测】
1、看图填空
①、∵AE是△ABC的角平分线
∴∠
=∠
=
∠
(
)
②、∵AF是△ABC的中线,
∴
=
=
(
③、∵AG是△ABC的高线,
∴∠
=∠
=90°(
)
2、如图∠ACE=∠BCE,BD=CD,指出图中三角形的特殊线段。
3.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B
落在点B′的位置,则线段AC具有性质(
)
A.是边BB′上的中线
B.是边BB′上的高
C.是∠BAB′的角平分线
D.以上三种性质合一
4、如图,在ΔABC中,AE是BAC的平分线,AD是BC的高,且
B=50°,
C=60°,则
EAD的度数是(
)
(A)35(B)25(C)15(D)5
5/如图,在⊿ABC中,
∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法那些是正确的,哪些是错误的
.
①AD是⊿ABE的角平分线
(
)
②BE是⊿ABD边AD上的中线
(
)
③BE是⊿ABC边AC上的中线
(
)
④CH是⊿ACD边AD上的高
(
)
6、如图2所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是(
)
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BD=EC
D.∠C的对边是DE
【课后作业】
一、单选题
1.不一定在三角形内部的线段是( )
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.以上皆不对
2.画△ABC中BC边上的高,下面的画法中,正确的是( )
A.
B.
C.
D.
3.已知BD是的中线,,且的周长为11,则的周长是(
)
A.9
B.14
C.16
D.不能确定
4.如图,D,E,F分别是边BC,AD,AC上的中点,若S阴影的面积为3,则△ABC的面积是( )
A.5
B.6
C.7
D.8
5.如图,三角形ABC中,D为BC上的一点,且S△ABD=S△ADC,则AD为(
)
A.高
B.角平分线
C.中线
D.不能确定
6.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
A.BC是△ABC的高
B.AC是△ABE的高
C.DE是△ABE的高
D.AD是△ACD的高
7.如图,在△ABC中,过点A作射线AD∥BC,点D不与点A重合,且AD≠BC,连结BD交AC于点O,连结CD,设△ABO、△ADO、△CDO和△BCO的面积分别为和,则下列说法不正确的是(
)
A.
B.
C.
D.
8.下列说法错误的是(
)
A.三角形三条高交于三角形内一点
B.三角形三条中线交于三角形内一点
C.三角形三条角平分线交于三角形内一点
D.三角形的中线、角平分线、高都是线段
9.如图AD⊥BC于点D,那么图中以AD为高的三角形的个数有(
)
A.3
B.4
C.5
D.6
二、填空题
10.一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是___三角形.
11.如图,AD是△ABC的中线,CE是△ACD的中线,S△ACE=3cm2,则S△ABC=_____cm2.
12.如图,AD为△ABC中线,点G为重心,若AD=6,则AG=________?.
13.如图,已知△ABC的周长为27cm,AC=9cm,BC边上中线AD=6cm,△ABD周长为19cm,AB=__________
14.如图,以为高的三角形共有___________个.
15.如图,在△ABC中,AB=2019,AC=2010,AD为中线,则△ABD与△ACD的周长之差为________.
三、解答题
16.如图,画出△ABC的AC边上的高BD,再写出图中的直角三角形.
17.如图,中(),,边上中线把的周长分成和两部分,求和的长.
18.在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.
答案
1.C
2.D
3.A
4.D
5.C
6.C
7.D
8.A
9.D
10.直角
11.12cm2.
12.4
13.8
cm.
14.6
15.9
16.解:如图,BD即为所求作高线,
直角三角形有:Rt△ABD、Rt△BCD.
17.解:设AC=x,则AB=2x,
∵BD是中线,
∴AD=DC=,由题意得,
2x+=30,解得x=12,则AC=12,AB=24,
∴BC=20﹣×12=14.
18.∵CD⊥AB∴∠CDB=90°.
∵∠B=60°∴∠BCD=180°-∠CDB-∠B=30°.
∵∠A=20°∠B=60°∠A+∠B+∠ACB=180°∴∠ACB=100°.
∵CE是∠ACB的平分线∴∠BCE=∠ACB=50°
∴∠CEB=180°-∠BCE-∠B=70°
∠ECD=∠BCE-∠BCD=20°.
初中数学
年级
八年级
重难点
重点:
1.了解三角形的高、中线与角平分线的概念,
会用工具准确画出三角形的高、中线与角平分线.
2.了解三角形的三条高、三条中线与三条角平分线分别交于一点.
难点:
1.三角形平分线与角平分线的区别,三角形的高与垂线的区别.
2.钝角三角形高的画法.
3.不同的三角形三条高的位置关系.
【知识储备】
三角形的
重要线段意义图形表示法三角形
的高线从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段1.AD是△ABC的BC上的高线.
2.AD⊥BC于D.
3.∠ADB=∠ADC=90°.三角形
的中线三角形中,连结一个顶点和它对边中点的
线段1.AD是△ABC的BC上的中线.
2.BD=DC=BC.三角形的
角平分线三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段1.AD是△ABC的∠BAC的平分线.
2.∠1=∠2=∠BAC.
【结论一】:每个三角形都能画出三条高。
【结论一】:每个三角形都能画出三条高。
相同点:三角形的三条高交于同一点。
不同点:锐角三角形的三条高交于三角形内一点,直角三角形的三条高交于直角的顶点,钝角三角形的三条高交于三角形外一点。
【结论二】:无论哪种三角形,它们都有三条中线,并且这三条中线都交于一点,这一点都在三角形内部。三角形的中线将三角形的面积平均分成两份。三角形三条中线相交于一点,这个交点叫做三角形的重心。
【结论三】:无论哪种三角形,它们都有三条角平分线,并且这三条角平分线都交于一点,这一点都在三角形内部。
(1)什么叫三角形的高?三角形的高与垂线有何区别和联系?
三角形的高是从三角形的一个顶点向它对边所在的直线作垂线,顶点和垂足之间的线段,而从三角形一个顶点向它对边所在的直线作垂线这条垂线是直线.
(2)什么叫三角形的中线?连结两点的线段与过两点的直线有何区别和联系?
三角形的中线是连结一个顶点和它对边的中点的线段,
而过两点的直线有着本质的不同,一个代表的是线段,另一个却是直线.
(3)什么叫三角形的角平分线?三角形的角平分线与角平分线有何区别和联系?
三角形的角平分线是三角形的一个内角平分线与它的对边相交,
这个角顶点与交点之间的线段,而角平分线指的是一条射线.
三角形的高、中线和角平分线是代表线段还是代表射线或直线?
三角形的高、中线和角平分线都代表线段,
这些线段的一个端点是三角形的一个顶点,另一个端点在这个顶点的对边上.
【典例精析】
典例1
已知:钝角△ABC,请画出△ABC的角平分线BD,AB边上的中线和AC边上的高,并用字母表示.
典例2
如图,AC⊥BC,AC=3,BC=4,AB=5,则点C到AB的距离为_______.
【答案】B
【详解】解:以CE为高的三角形就是以C为一个顶点,再从B,F,E,D,A中任意选两个点组成,
∴4+3+2+1=10(个).
∴以CE为高的三角形有10个.
故选:B.
典例4
如图,三角形ABC中,D为BC上的一点,且S△ABD=S△ADC,则AD为(
)
A.高
B.角平分线
C.中线
D.不能确定
典例5.
如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
解:∵AD是BC边上的高,∠EAD=5°,∴∠AED=85°,∵∠B=50°,
∴∠BAE=∠AED﹣∠B=85°﹣50°=35°,∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=70°,∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°.
典例6.如图,为△ABC的中线,为的中线.
(1),,求的度数;
(2)若△ABC的面积为20,,求△BDE中边上的高.
解:(1)在中,
,,
;
(2)过点作边上的高,
为的中线,为的中线,
,
,
,
的面积为20,,
,
即:
,
;
典例7如图BO、CO分别平分和,DE过点D且,,,求的周长.
解∵BO、CO分别平分和,
,,
又.
,,
,,
,,
∴△ADE周长
【当堂小测】
1、看图填空
①、∵AE是△ABC的角平分线
∴∠
=∠
=
∠
(
)
②、∵AF是△ABC的中线,
∴
=
=
(
③、∵AG是△ABC的高线,
∴∠
=∠
=90°(
)
2、如图∠ACE=∠BCE,BD=CD,指出图中三角形的特殊线段。
3.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B
落在点B′的位置,则线段AC具有性质(
)
A.是边BB′上的中线
B.是边BB′上的高
C.是∠BAB′的角平分线
D.以上三种性质合一
4、如图,在ΔABC中,AE是BAC的平分线,AD是BC的高,且
B=50°,
C=60°,则
EAD的度数是(
)
(A)35(B)25(C)15(D)5
5/如图,在⊿ABC中,
∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法那些是正确的,哪些是错误的
.
①AD是⊿ABE的角平分线
(
)
②BE是⊿ABD边AD上的中线
(
)
③BE是⊿ABC边AC上的中线
(
)
④CH是⊿ACD边AD上的高
(
)
6、如图2所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是(
)
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BD=EC
D.∠C的对边是DE
【课后作业】
一、单选题
1.不一定在三角形内部的线段是( )
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.以上皆不对
2.画△ABC中BC边上的高,下面的画法中,正确的是( )
A.
B.
C.
D.
3.已知BD是的中线,,且的周长为11,则的周长是(
)
A.9
B.14
C.16
D.不能确定
4.如图,D,E,F分别是边BC,AD,AC上的中点,若S阴影的面积为3,则△ABC的面积是( )
A.5
B.6
C.7
D.8
5.如图,三角形ABC中,D为BC上的一点,且S△ABD=S△ADC,则AD为(
)
A.高
B.角平分线
C.中线
D.不能确定
6.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
A.BC是△ABC的高
B.AC是△ABE的高
C.DE是△ABE的高
D.AD是△ACD的高
7.如图,在△ABC中,过点A作射线AD∥BC,点D不与点A重合,且AD≠BC,连结BD交AC于点O,连结CD,设△ABO、△ADO、△CDO和△BCO的面积分别为和,则下列说法不正确的是(
)
A.
B.
C.
D.
8.下列说法错误的是(
)
A.三角形三条高交于三角形内一点
B.三角形三条中线交于三角形内一点
C.三角形三条角平分线交于三角形内一点
D.三角形的中线、角平分线、高都是线段
9.如图AD⊥BC于点D,那么图中以AD为高的三角形的个数有(
)
A.3
B.4
C.5
D.6
二、填空题
10.一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是___三角形.
11.如图,AD是△ABC的中线,CE是△ACD的中线,S△ACE=3cm2,则S△ABC=_____cm2.
12.如图,AD为△ABC中线,点G为重心,若AD=6,则AG=________?.
13.如图,已知△ABC的周长为27cm,AC=9cm,BC边上中线AD=6cm,△ABD周长为19cm,AB=__________
14.如图,以为高的三角形共有___________个.
15.如图,在△ABC中,AB=2019,AC=2010,AD为中线,则△ABD与△ACD的周长之差为________.
三、解答题
16.如图,画出△ABC的AC边上的高BD,再写出图中的直角三角形.
17.如图,中(),,边上中线把的周长分成和两部分,求和的长.
18.在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.
答案
1.C
2.D
3.A
4.D
5.C
6.C
7.D
8.A
9.D
10.直角
11.12cm2.
12.4
13.8
cm.
14.6
15.9
16.解:如图,BD即为所求作高线,
直角三角形有:Rt△ABD、Rt△BCD.
17.解:设AC=x,则AB=2x,
∵BD是中线,
∴AD=DC=,由题意得,
2x+=30,解得x=12,则AC=12,AB=24,
∴BC=20﹣×12=14.
18.∵CD⊥AB∴∠CDB=90°.
∵∠B=60°∴∠BCD=180°-∠CDB-∠B=30°.
∵∠A=20°∠B=60°∠A+∠B+∠ACB=180°∴∠ACB=100°.
∵CE是∠ACB的平分线∴∠BCE=∠ACB=50°
∴∠CEB=180°-∠BCE-∠B=70°
∠ECD=∠BCE-∠BCD=20°.
