人教版八年级上册 11.2.1 三角形的内角教案
文档属性
| 名称 | 人教版八年级上册 11.2.1 三角形的内角教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 552.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 00:00:00 | ||
图片预览



文档简介
第八.四讲--三角形的内角
初中数学
年级
八年级
重难点
教学重点:三角形内角和定理及应用。
教学难点:三角形内角和定理证明中辅助线的添加。
知识点一:三角形内角和定理
1、三角形三边满足什么关系?(两边之和大于第三边,两之差小于第三边)。
那么三角形的三个内角有什么关系?你有什么方法得出答案?
答:(1)用量角器量180°。
???
(2)用折纸把三个内角拼在一起。
???
(3)将三角形纸片两个内角剪下拼成一个平角。
小结:我们不能对所有的三角形都进行拼图实验,这需要我们利用所学的知识去证明。
分析证明思路
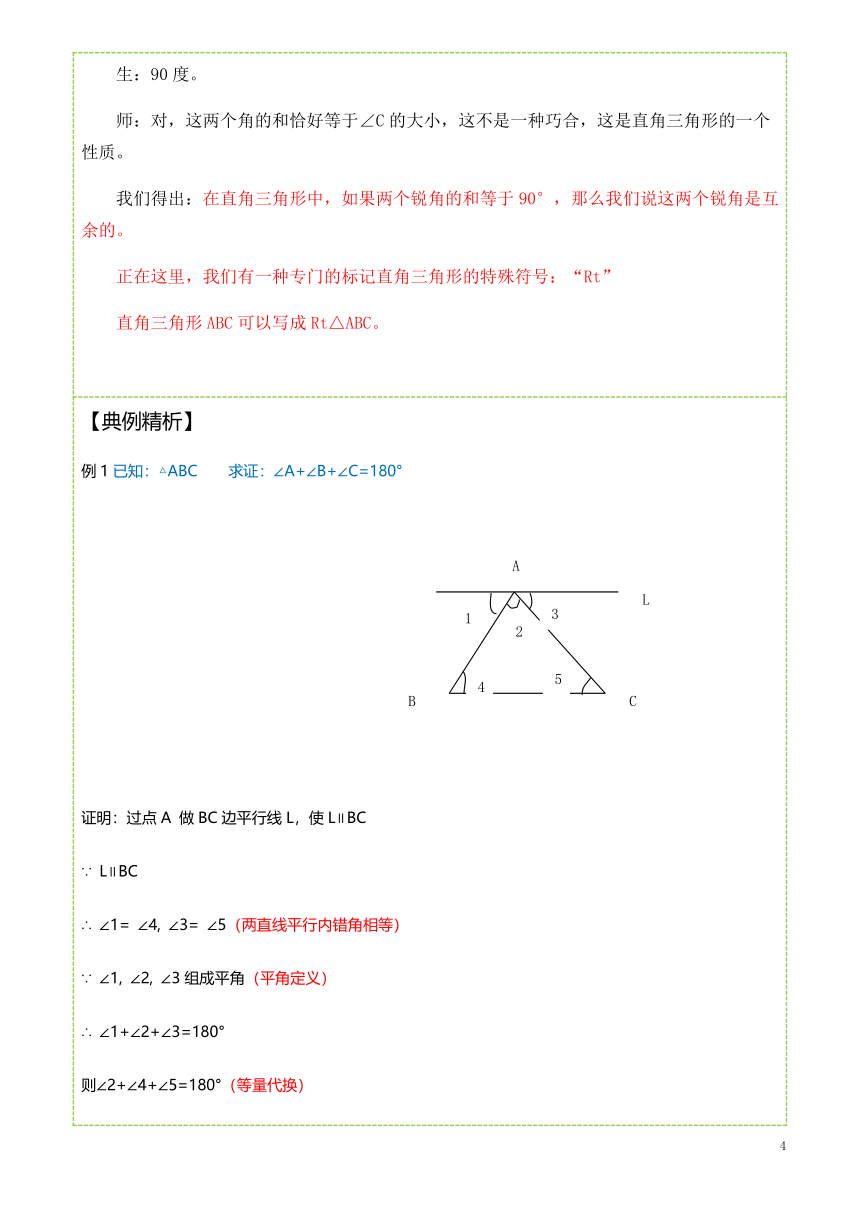
已知:△ABC求证∠A+∠B+∠C=180°
分析:此题显然是要作辅助线,根据刚才平移角的思路。方法如下
证明:延长BC到D,作CF∥BA?
∴∠ACF=∠A,∠FCD=∠B
???∵?∠ACF+∠FCD+∠ACB=180°
???∴∠A+∠B+∠ACB=180°
另外还有一种作辅助线的方法,学生可以课外证明?
?(1)过A作BC的平行线,图如下?
教师组织学生讨论,放手让学生证明。(证明略)
2、经过证明,发现三角形内角和定理
(1?)定理:三角形内和等于180°。
即????∠A+∠B+∠C=180°
(2?)作用:它是三角形三个内角必须满足的条件;它实际上提供了三个内角满足的?一个等量关系,是求三角形时常用的一个条件。
(3?)定理形式的变形:
①∠A?=?180°?―∠B―∠C????????;??????
?②∠B?+?∠?C?=180?°?-?∠A???????。
3、按角对三角形进行分类
三角形中能有几个钝角?几个直角?几个锐角?
(得出三个概念:钝角三角形、直角三角形、锐角三角形)。
判断下列说法是否正确
三角形的三个内角中,最多有一个是钝角。
三角形的三个内角中至少有两个是锐角。
直角三角形的两个锐角是互余的。
得出推论:直角三角形的两个锐角互余。
知识点二:互余定理。
如图,在直角三角形ABC中,∠C=90°,由三角形内角和定理,得
∠A+∠B+∠C=180°,即∠A+∠B+90°=180°,所以∠A+∠B=90°
我们以此可以看出,三角形内角和定理在直角三角形中也是适用的,成立。
从上面我们可以得出:∠A+∠B的和是多少?
生:90度。
师:对,这两个角的和恰好等于∠C的大小,这不是一种巧合,这是直角三角形的一个性质。
我们得出:在直角三角形中,如果两个锐角的和等于90°,那么我们说这两个锐角是互余的。
正在这里,我们有一种专门的标记直角三角形的特殊符号:“Rt”
直角三角形ABC可以写成Rt△ABC。
【典例精析】
例1已知:△ABC
求证:∠A+∠B+∠C=180°
?
证明:过点A
做BC边平行线L,使L∥BC
∵
L∥BC
∴
∠1=
∠4,
∠3=
∠5(两直线平行内错角相等)
∵
∠1,
∠2,
∠3组成平角(平角定义)
∴
∠1+∠2+∠3=180°
则∠2+∠4+∠5=180°(等量代换)
三角形内角和等于180°
例2
图8
如图8,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,求∠ADB的度数.
解:由∠BAC=40°,AD是△ABC的角平分线,得∠BAD=∠BAC=20°.
在△ABD中,∠ADB=180°-∠B-∠BAD=180°-75°-20°=85°.
图9
例3
如图9是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?
解:∠CAB=∠BAD-∠CAD=80°-50°=30°.
∵
AD∥BE,∴
∠BAD+∠ABE=180°.
∴
∠ABE=180°-∠BAD=180°-80°=100°.
∴
∠ABC=∠ABE-∠EBC=100°-40°=60°.
在△ABC中,∠ACB=180°-∠ABC-∠CAB=180°-60°-30°=90°.?
答:从B岛看A、C两岛的视角∠ABC是60°,从C岛看A、B两岛的视角∠ACB是90°.
图10
例4
如图10所示,∠C=∠D=90°,AD,BC相交于点E.∠CAE与∠DBE有什么关系?
解:在Rt△ACE中,∠CAE=90°-∠AEC.?
在Rt△BDE中,∠DBE=90°-∠BED.
∵
∠AEC=∠BED,∴
∠CAE=∠DBE.
例5:已知三角形三个内角的度数之比为2:3:7,求这三个内角的度数。
解:设三个内角度数分别为:2x、3x、7x,
由三角形内角和为180°,得:2x+3x+7x=180°
所以三个内角度数分别为30°,45°,105°。
【当堂小测】
1、如图,直线l1∥l2,∠1=35°,∠2=80°,则∠3等于( )
A.55°
B.60°
C.65°
D.70°
2、
如图,AB∥CD,点E在线段BC上,CD=CE,若∠D=75°,则∠B的数为(
)
A.25°
B.30°
C.40°
D.50°
3、如图,
在△ABC中,
BD、CE分别平分∠ABC和∠ACB.
1).若∠A=60°,求∠BOC的度数.
2).若∠A=α,求∠BOC的度数.
【课后作业】
1、
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.
(1)则∠BAE=
;
(2)求∠DAE的度数.
2、在Rt△ABE中,∠AEB=90°,C为AE延长线上的一点,D为AB边上的一点,DC交BE于F,若∠ADC=80°,∠B=30°,求∠C的度数.
初中数学
年级
八年级
重难点
教学重点:三角形内角和定理及应用。
教学难点:三角形内角和定理证明中辅助线的添加。
知识点一:三角形内角和定理
1、三角形三边满足什么关系?(两边之和大于第三边,两之差小于第三边)。
那么三角形的三个内角有什么关系?你有什么方法得出答案?
答:(1)用量角器量180°。
???
(2)用折纸把三个内角拼在一起。
???
(3)将三角形纸片两个内角剪下拼成一个平角。
小结:我们不能对所有的三角形都进行拼图实验,这需要我们利用所学的知识去证明。
分析证明思路
已知:△ABC求证∠A+∠B+∠C=180°
分析:此题显然是要作辅助线,根据刚才平移角的思路。方法如下
证明:延长BC到D,作CF∥BA?
∴∠ACF=∠A,∠FCD=∠B
???∵?∠ACF+∠FCD+∠ACB=180°
???∴∠A+∠B+∠ACB=180°
另外还有一种作辅助线的方法,学生可以课外证明?
?(1)过A作BC的平行线,图如下?
教师组织学生讨论,放手让学生证明。(证明略)
2、经过证明,发现三角形内角和定理
(1?)定理:三角形内和等于180°。
即????∠A+∠B+∠C=180°
(2?)作用:它是三角形三个内角必须满足的条件;它实际上提供了三个内角满足的?一个等量关系,是求三角形时常用的一个条件。
(3?)定理形式的变形:
①∠A?=?180°?―∠B―∠C????????;??????
?②∠B?+?∠?C?=180?°?-?∠A???????。
3、按角对三角形进行分类
三角形中能有几个钝角?几个直角?几个锐角?
(得出三个概念:钝角三角形、直角三角形、锐角三角形)。
判断下列说法是否正确
三角形的三个内角中,最多有一个是钝角。
三角形的三个内角中至少有两个是锐角。
直角三角形的两个锐角是互余的。
得出推论:直角三角形的两个锐角互余。
知识点二:互余定理。
如图,在直角三角形ABC中,∠C=90°,由三角形内角和定理,得
∠A+∠B+∠C=180°,即∠A+∠B+90°=180°,所以∠A+∠B=90°
我们以此可以看出,三角形内角和定理在直角三角形中也是适用的,成立。
从上面我们可以得出:∠A+∠B的和是多少?
生:90度。
师:对,这两个角的和恰好等于∠C的大小,这不是一种巧合,这是直角三角形的一个性质。
我们得出:在直角三角形中,如果两个锐角的和等于90°,那么我们说这两个锐角是互余的。
正在这里,我们有一种专门的标记直角三角形的特殊符号:“Rt”
直角三角形ABC可以写成Rt△ABC。
【典例精析】
例1已知:△ABC
求证:∠A+∠B+∠C=180°
?
证明:过点A
做BC边平行线L,使L∥BC
∵
L∥BC
∴
∠1=
∠4,
∠3=
∠5(两直线平行内错角相等)
∵
∠1,
∠2,
∠3组成平角(平角定义)
∴
∠1+∠2+∠3=180°
则∠2+∠4+∠5=180°(等量代换)
三角形内角和等于180°
例2
图8
如图8,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,求∠ADB的度数.
解:由∠BAC=40°,AD是△ABC的角平分线,得∠BAD=∠BAC=20°.
在△ABD中,∠ADB=180°-∠B-∠BAD=180°-75°-20°=85°.
图9
例3
如图9是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?
解:∠CAB=∠BAD-∠CAD=80°-50°=30°.
∵
AD∥BE,∴
∠BAD+∠ABE=180°.
∴
∠ABE=180°-∠BAD=180°-80°=100°.
∴
∠ABC=∠ABE-∠EBC=100°-40°=60°.
在△ABC中,∠ACB=180°-∠ABC-∠CAB=180°-60°-30°=90°.?
答:从B岛看A、C两岛的视角∠ABC是60°,从C岛看A、B两岛的视角∠ACB是90°.
图10
例4
如图10所示,∠C=∠D=90°,AD,BC相交于点E.∠CAE与∠DBE有什么关系?
解:在Rt△ACE中,∠CAE=90°-∠AEC.?
在Rt△BDE中,∠DBE=90°-∠BED.
∵
∠AEC=∠BED,∴
∠CAE=∠DBE.
例5:已知三角形三个内角的度数之比为2:3:7,求这三个内角的度数。
解:设三个内角度数分别为:2x、3x、7x,
由三角形内角和为180°,得:2x+3x+7x=180°
所以三个内角度数分别为30°,45°,105°。
【当堂小测】
1、如图,直线l1∥l2,∠1=35°,∠2=80°,则∠3等于( )
A.55°
B.60°
C.65°
D.70°
2、
如图,AB∥CD,点E在线段BC上,CD=CE,若∠D=75°,则∠B的数为(
)
A.25°
B.30°
C.40°
D.50°
3、如图,
在△ABC中,
BD、CE分别平分∠ABC和∠ACB.
1).若∠A=60°,求∠BOC的度数.
2).若∠A=α,求∠BOC的度数.
【课后作业】
1、
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.
(1)则∠BAE=
;
(2)求∠DAE的度数.
2、在Rt△ABE中,∠AEB=90°,C为AE延长线上的一点,D为AB边上的一点,DC交BE于F,若∠ADC=80°,∠B=30°,求∠C的度数.
