人教版上册 八年级数学 13.1.3 线段的垂直平分线有关作图 课件(共15张PPT)
文档属性
| 名称 | 人教版上册 八年级数学 13.1.3 线段的垂直平分线有关作图 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 785.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
§13.1.3
线段垂直平分线有关作图
第十三章
轴对称
13.1
轴对称
知识回顾
P
A
B
l
C
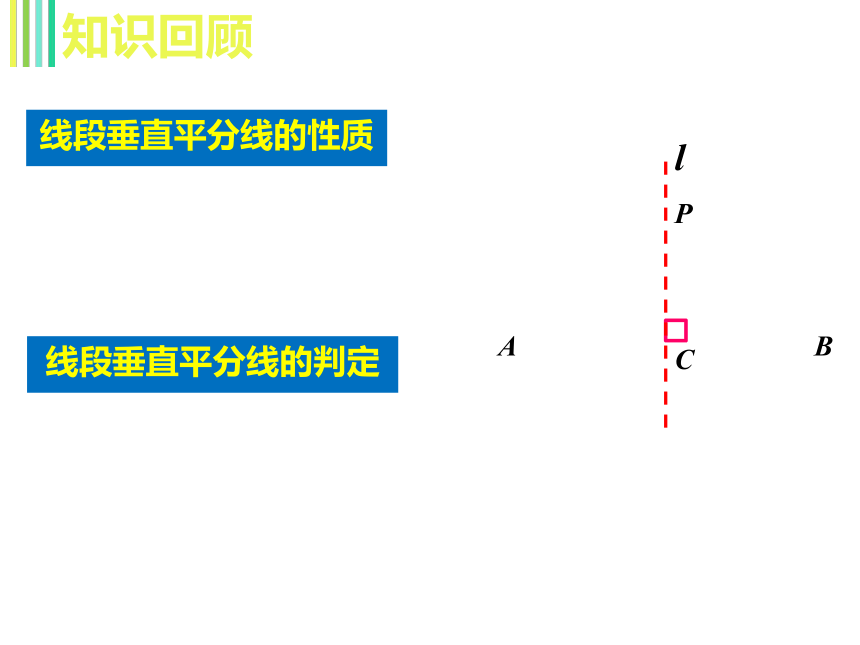
线段垂直平分线的性质
∵点P
在AB
的垂直平分线上
∴PA
=PB
线段垂直平分线的判定
∵PA
=PB,
∴点P
在AB
的垂直平分线上.
巩固练习
【例1】已知:如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BE=CF,
求证:AD是BC的中垂线.
证明:
∵AD是△ABC的角平分线,
DE⊥AB,DF⊥AC,
∴DE=DF.
在△BED和△CFD中,
DE=DF,
∠BED=∠CFD=90°,
BE=CF
∴△BED≌△CFD(SAS).
∴∠B=∠C,BD=CD.
在△ABD和△ACD中,
∠BAD=∠CAD,
∠B=∠C,
AD=AD,
∴△ABD≌△ACD(AAS).
∴∠ADB=∠ADC=90°.
∴AD是BC的中垂线.
巩固练习
1.如图,已知E为∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为点C,D.求证:OE垂直平分CD.
证明:∵点E在∠AOB的平分线上,
ED⊥OB,EC⊥OA,
∴ED=EC.
在Rt△EDO和Rt△ECO中,
ED=EC,
OE=OE,
∴Rt△EDO≌Rt△ECO(HL).
∴OD=OC.
∴点O,E在CD的垂直平分线上.
∴OE垂直平分CD.
探究新知
a
A
B
C
A
′
B
′
C
′
m
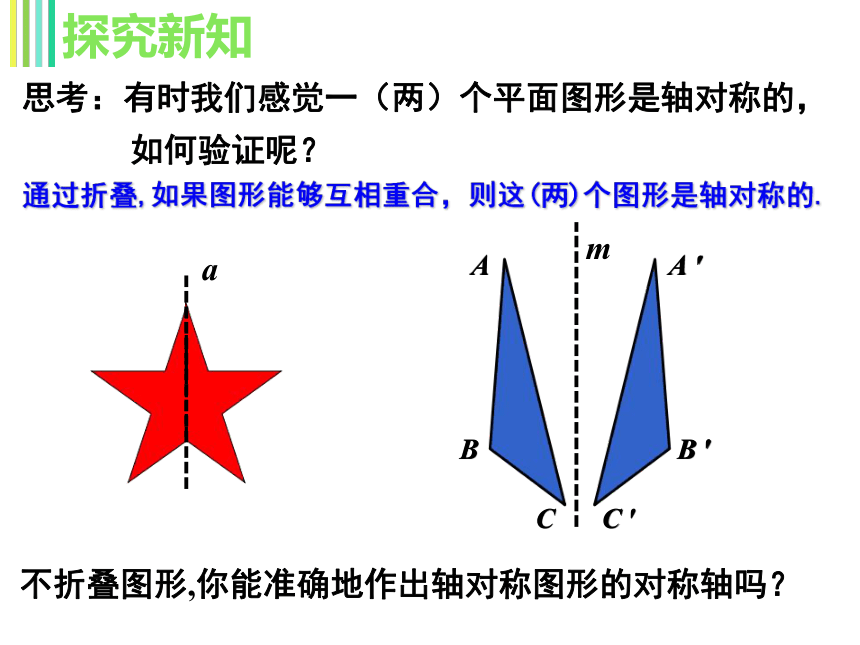
思考:有时我们感觉一(两)个平面图形是轴对称的,
如何验证呢?
通过折叠,如果图形能够互相重合,则这(两)个图形是轴对称的.
不折叠图形,你能准确地作出轴对称图形的对称轴吗?
例题讲解
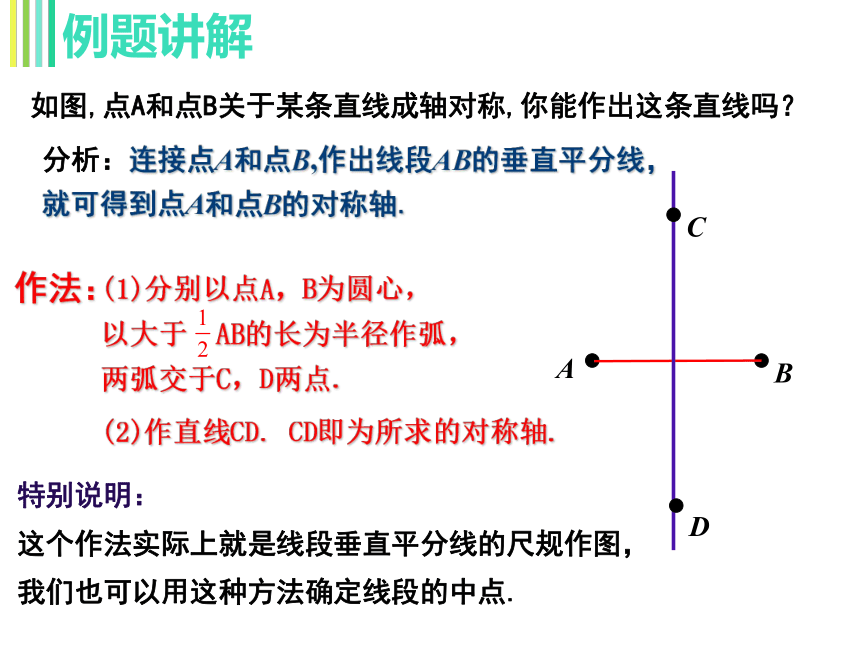
如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?
分析:连接点A和点B,作出线段AB的垂直平分线,
就可得到点A和点B的对称轴.
A
B
C
D
作法:
(1)分别以点A,B为圆心,
以大于
AB的长为半径作弧,
两弧交于C,D两点.
(2)作直线CD.
CD即为所求的对称轴.
特别说明:
这个作法实际上就是线段垂直平分线的尺规作图,
我们也可以用这种方法确定线段的中点.
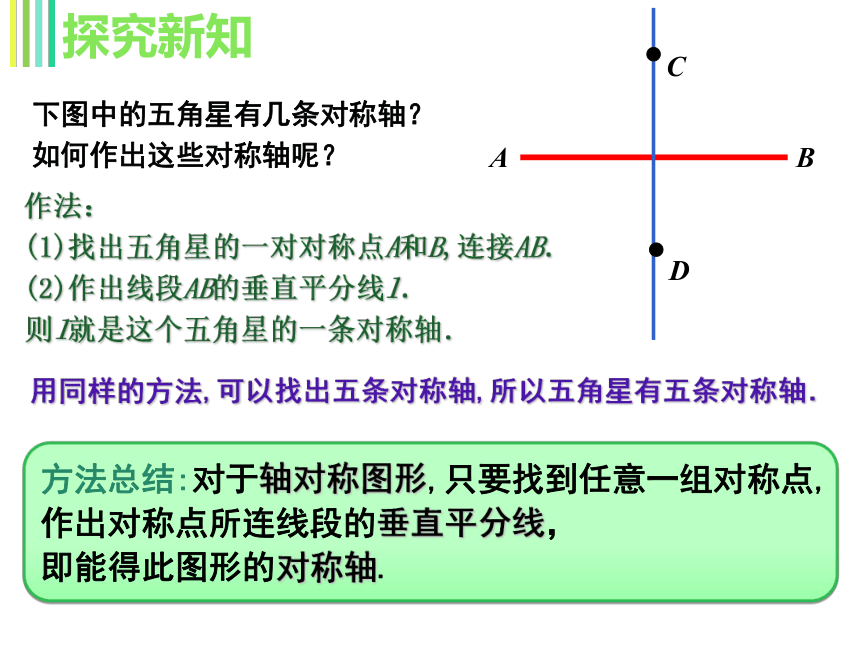
作法:
(1)找出五角星的一对对称点A和B,连接AB.
(2)作出线段AB的垂直平分线l.
则l就是这个五角星的一条对称轴.
探究新知
下图中的五角星有几条对称轴?
如何作出这些对称轴呢?
A
B
用同样的方法,可以找出五条对称轴,所以五角星有五条对称轴.
C
D
方法总结:对于轴对称图形,只要找到任意一组对称点,作出对称点所连线段的垂直平分线,
即能得此图形的对称轴.
巩固练习
【例2】如图,△ABC与△A'B'C'关于某条直线对称,
请作出这条直线.
解:
如图所示,作法如下.
①分别以点B,B′为圆心,
以大于BB′的一半的长为半径画弧,
两弧交于M,N两点;
②连接MN,则MN即为所求的直线.
巩固练习
【例2】如图,△ABC与△A'B'C'关于某条直线对称,
请作出这条直线.
解:
如图所示,作法如下.
①分别以点B,B′为圆心,
以大于BB′的一半的长为半径画弧,
两弧交于M,N两点;
②连接MN,则MN即为所求的直线.
巩固练习
2.如图,△ABC和△DEF关于直线l成轴对称,请作出直线l.
解:
如图所示。
巩固练习
2.如图,△ABC和△DEF关于直线l成轴对称,请作出直线l.
解:
如图所示。
课堂小结
线段的垂直
平分线的
有关作图
尺规作图
作对称轴的常见方法
属于基本作图之一,必须熟熟练掌握
(1)将图形对折;
(2)用尺规作图;
课堂小结
1.在直线、角、线段、等边三角形四个图形中,
对称轴最多的是______,它有______条对称轴;
最少的是______,它有______条对称轴.
2.
点O是△ABC的三条边的垂直平分线的交点,OA=8,
则OA+OB+OC的值是( )
A.
11
B.
16
C.
24
D.
64
3.
圆是轴对称图形,它的对称轴有( )
A.1条 B.2条
C.3条 D.无数条
直线
无数
角
1
C
D
课堂小结
4.如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ACF=48°,
则∠ABC的度数为( )
A.
48° B.
36°
C.
30° D.
24°
5.在如图所示的网格中,能找出
与A,B两点构成以AB为底边的
等腰三角形的格点数有( )
A.1个 B.2个
C.3个 D.4个
A
D
填写P46
“课前预习”
预习课本P67-68
《学导练》P44-45
作业
《课堂小测本》P135-136
§13.1.3
线段垂直平分线有关作图
第十三章
轴对称
13.1
轴对称
知识回顾
P
A
B
l
C
线段垂直平分线的性质
∵点P
在AB
的垂直平分线上
∴PA
=PB
线段垂直平分线的判定
∵PA
=PB,
∴点P
在AB
的垂直平分线上.
巩固练习
【例1】已知:如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BE=CF,
求证:AD是BC的中垂线.
证明:
∵AD是△ABC的角平分线,
DE⊥AB,DF⊥AC,
∴DE=DF.
在△BED和△CFD中,
DE=DF,
∠BED=∠CFD=90°,
BE=CF
∴△BED≌△CFD(SAS).
∴∠B=∠C,BD=CD.
在△ABD和△ACD中,
∠BAD=∠CAD,
∠B=∠C,
AD=AD,
∴△ABD≌△ACD(AAS).
∴∠ADB=∠ADC=90°.
∴AD是BC的中垂线.
巩固练习
1.如图,已知E为∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为点C,D.求证:OE垂直平分CD.
证明:∵点E在∠AOB的平分线上,
ED⊥OB,EC⊥OA,
∴ED=EC.
在Rt△EDO和Rt△ECO中,
ED=EC,
OE=OE,
∴Rt△EDO≌Rt△ECO(HL).
∴OD=OC.
∴点O,E在CD的垂直平分线上.
∴OE垂直平分CD.
探究新知
a
A
B
C
A
′
B
′
C
′
m
思考:有时我们感觉一(两)个平面图形是轴对称的,
如何验证呢?
通过折叠,如果图形能够互相重合,则这(两)个图形是轴对称的.
不折叠图形,你能准确地作出轴对称图形的对称轴吗?
例题讲解
如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?
分析:连接点A和点B,作出线段AB的垂直平分线,
就可得到点A和点B的对称轴.
A
B
C
D
作法:
(1)分别以点A,B为圆心,
以大于
AB的长为半径作弧,
两弧交于C,D两点.
(2)作直线CD.
CD即为所求的对称轴.
特别说明:
这个作法实际上就是线段垂直平分线的尺规作图,
我们也可以用这种方法确定线段的中点.
作法:
(1)找出五角星的一对对称点A和B,连接AB.
(2)作出线段AB的垂直平分线l.
则l就是这个五角星的一条对称轴.
探究新知
下图中的五角星有几条对称轴?
如何作出这些对称轴呢?
A
B
用同样的方法,可以找出五条对称轴,所以五角星有五条对称轴.
C
D
方法总结:对于轴对称图形,只要找到任意一组对称点,作出对称点所连线段的垂直平分线,
即能得此图形的对称轴.
巩固练习
【例2】如图,△ABC与△A'B'C'关于某条直线对称,
请作出这条直线.
解:
如图所示,作法如下.
①分别以点B,B′为圆心,
以大于BB′的一半的长为半径画弧,
两弧交于M,N两点;
②连接MN,则MN即为所求的直线.
巩固练习
【例2】如图,△ABC与△A'B'C'关于某条直线对称,
请作出这条直线.
解:
如图所示,作法如下.
①分别以点B,B′为圆心,
以大于BB′的一半的长为半径画弧,
两弧交于M,N两点;
②连接MN,则MN即为所求的直线.
巩固练习
2.如图,△ABC和△DEF关于直线l成轴对称,请作出直线l.
解:
如图所示。
巩固练习
2.如图,△ABC和△DEF关于直线l成轴对称,请作出直线l.
解:
如图所示。
课堂小结
线段的垂直
平分线的
有关作图
尺规作图
作对称轴的常见方法
属于基本作图之一,必须熟熟练掌握
(1)将图形对折;
(2)用尺规作图;
课堂小结
1.在直线、角、线段、等边三角形四个图形中,
对称轴最多的是______,它有______条对称轴;
最少的是______,它有______条对称轴.
2.
点O是△ABC的三条边的垂直平分线的交点,OA=8,
则OA+OB+OC的值是( )
A.
11
B.
16
C.
24
D.
64
3.
圆是轴对称图形,它的对称轴有( )
A.1条 B.2条
C.3条 D.无数条
直线
无数
角
1
C
D
课堂小结
4.如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ACF=48°,
则∠ABC的度数为( )
A.
48° B.
36°
C.
30° D.
24°
5.在如图所示的网格中,能找出
与A,B两点构成以AB为底边的
等腰三角形的格点数有( )
A.1个 B.2个
C.3个 D.4个
A
D
填写P46
“课前预习”
预习课本P67-68
《学导练》P44-45
作业
《课堂小测本》P135-136
