人教版上册八年级数学13.2.1 画轴对称图形 课件(共15张PPT)
文档属性
| 名称 | 人教版上册八年级数学13.2.1 画轴对称图形 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 425.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 00:00:00 | ||
图片预览

文档简介
(共15张PPT)
§13.2.1
画轴对称图形
第十三章
轴对称
13.2
画对称图形
情景导入
探究新知
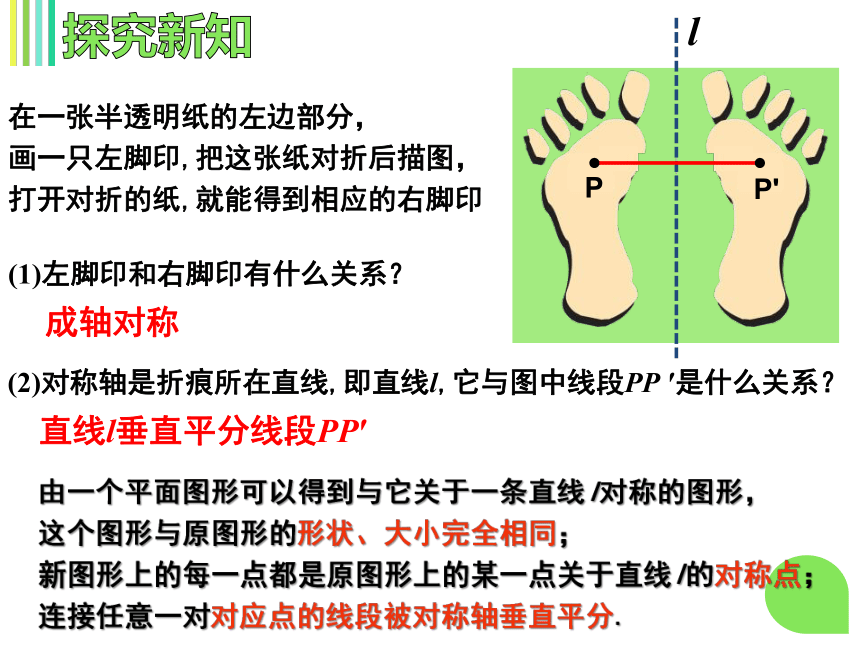
在一张半透明纸的左边部分,
画一只左脚印,把这张纸对折后描图,
打开对折的纸,就能得到相应的右脚印
(1)左脚印和右脚印有什么关系?
成轴对称
(2)对称轴是折痕所在直线,即直线l,它与图中线段PP
′是什么关系?
直线l垂直平分线段PP′
P
P'
由一个平面图形可以得到与它关于一条直线l对称的图形,
这个图形与原图形的形状、大小完全相同;
新图形上的每一点都是原图形上的某一点关于直线l的对称点;
连接任意一对对应点的线段被对称轴垂直平分.
探究新知
如何画一个点的轴对称图形?
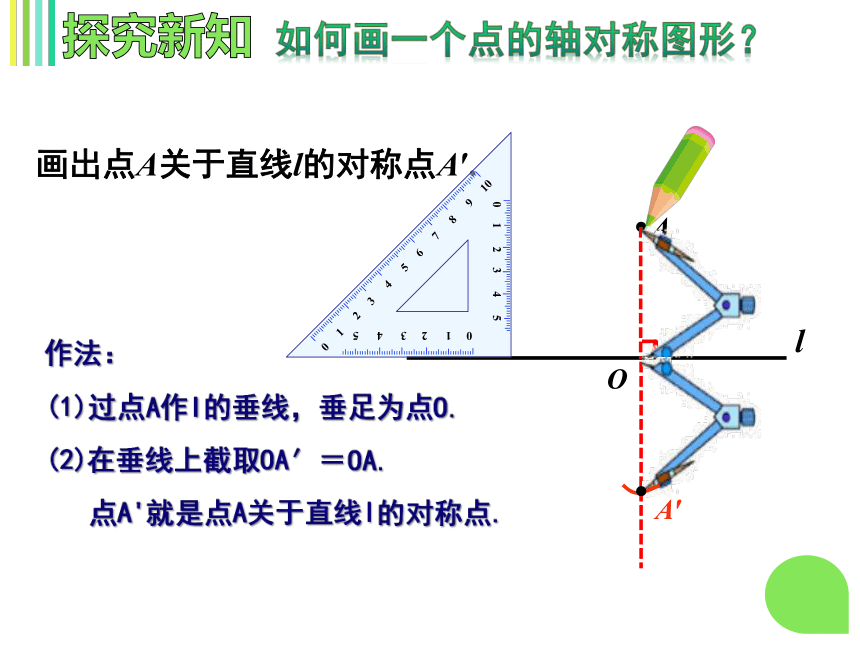
画出点A关于直线l的对称点A′.
l
A
A′
O
作法:
(1)过点A作l的垂线,垂足为点O.
(2)在垂线上截取OA′=OA.
点A'就是点A关于直线l的对称点.
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
探究新知
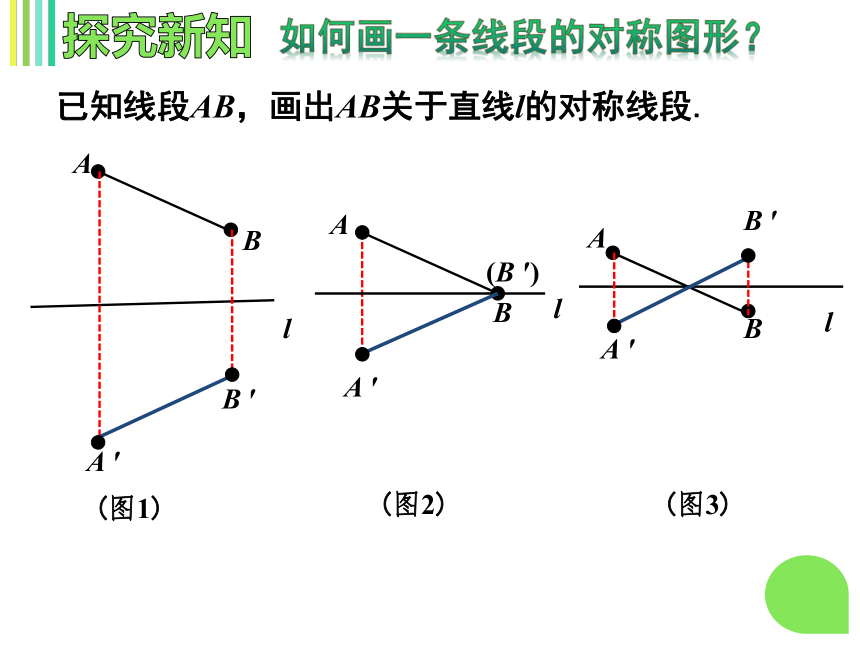
如何画一条线段的对称图形?
已知线段AB,画出AB关于直线l的对称线段.
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A
′
A
′
A
′
B
′
(B
′)
B
′
探究新知
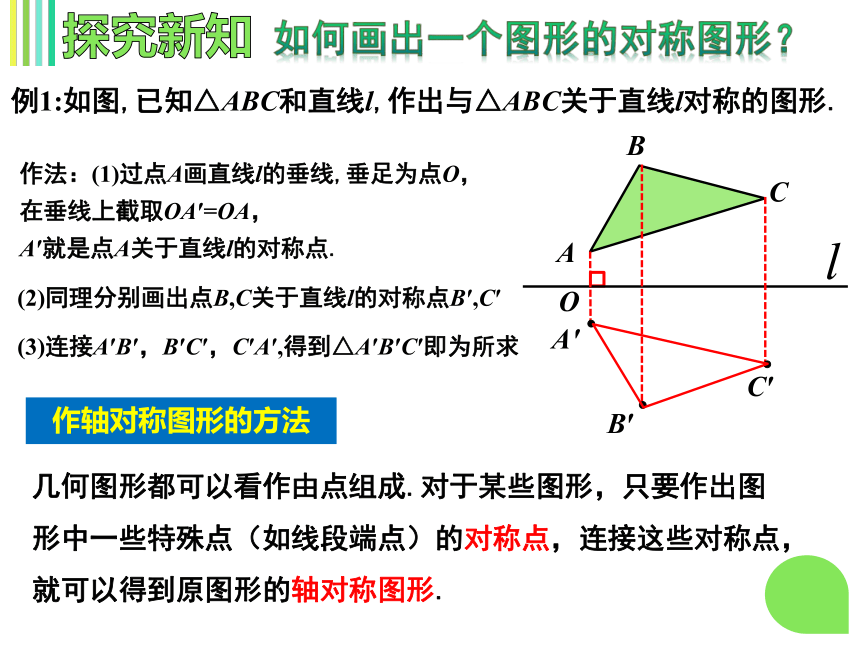
如何画出一个图形的对称图形?
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
作法:(1)过点A画直线l的垂线,垂足为点O,
在垂线上截取OA′=OA,
A′就是点A关于直线l的对称点.
(3)连接A′B′,B′C′,C′A′,得到△A′B′C′即为所求
(2)同理分别画出点B,C关于直线l的对称点B′,C′
A
B
C
A′
B′
C′
O
作轴对称图形的方法
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
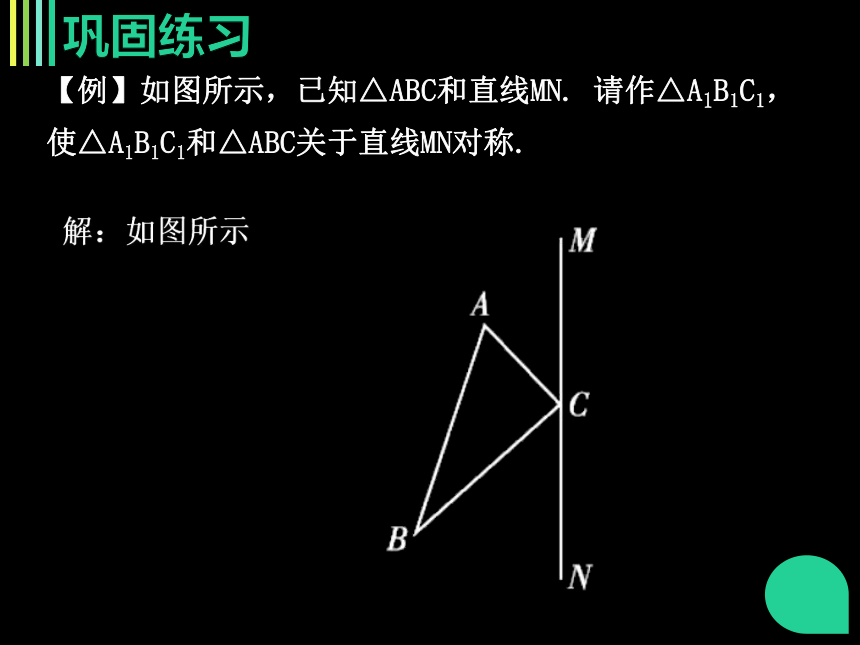
巩固练习
【例】如图所示,已知△ABC和直线MN.
请作△A1B1C1,
使△A1B1C1和△ABC关于直线MN对称.
解:如图所示
巩固练习
【例】如图所示,已知△ABC和直线MN.
请作△A1B1C1,
使△A1B1C1和△ABC关于直线MN对称.
解:如图所示,作法如下.
巩固练习
利用轴对称知识画图:
(1)作出图形AOCB关于直线a,b对称的图形,围成一个封闭图形;
(2)由(1)得到的星形图形中有_____条对称轴;
(3)用剪刀剪出这个星形图,正方形纸片需要对折___次.(只剪一刀)
4
3
解:(1)如图所示.
巩固练习
利用轴对称知识画图:
(1)作出图形AOCB关于直线a,b对称的图形,围成一个封闭图形;
(2)由(1)得到的星形图形中有_____条对称轴;
(3)用剪刀剪出这个星形图,正方形纸片需要对折___次.(只剪一刀)
4
3
解:(1)如图所示.
巩固练习
P68
T1.如图,把下列图形补成关于直线l的对称图形.
课堂小结
画轴对称图形
作图原理
作图方法
对称轴是对称点连线段的垂直平分线.
(1)找特征点;
(2)作垂线;
(3)截取等长;
(4)依次连线.
课堂小结
1.
成轴对称的两个图形中的任何一个都可以看作是___________________________得到的.
经过轴对称变换后的图形和原图形的_____、_____完全相同,连接任意一对对应点的线段都被对称轴__________.
2.
观察规律并填空:
.
3.
下列图形中,点P与P′关于直线MN对称的是(
)
另一个图形经过轴对称变换
大小
形状
垂直平分
D
课堂小结
4.
作已知点关于某直线的对称点的第一步是(
)
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
5.
下列各组图形中,其中一个图形能由另一个图形通过轴对称变换得到的是(
)
B
C
15
《学导练》P47-48
暗线本A:
P55
T5、P56
T11
请输入标题文字
《课堂小测本》P137
作业
§13.2.1
画轴对称图形
第十三章
轴对称
13.2
画对称图形
情景导入
探究新知
在一张半透明纸的左边部分,
画一只左脚印,把这张纸对折后描图,
打开对折的纸,就能得到相应的右脚印
(1)左脚印和右脚印有什么关系?
成轴对称
(2)对称轴是折痕所在直线,即直线l,它与图中线段PP
′是什么关系?
直线l垂直平分线段PP′
P
P'
由一个平面图形可以得到与它关于一条直线l对称的图形,
这个图形与原图形的形状、大小完全相同;
新图形上的每一点都是原图形上的某一点关于直线l的对称点;
连接任意一对对应点的线段被对称轴垂直平分.
探究新知
如何画一个点的轴对称图形?
画出点A关于直线l的对称点A′.
l
A
A′
O
作法:
(1)过点A作l的垂线,垂足为点O.
(2)在垂线上截取OA′=OA.
点A'就是点A关于直线l的对称点.
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
探究新知
如何画一条线段的对称图形?
已知线段AB,画出AB关于直线l的对称线段.
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A
′
A
′
A
′
B
′
(B
′)
B
′
探究新知
如何画出一个图形的对称图形?
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
作法:(1)过点A画直线l的垂线,垂足为点O,
在垂线上截取OA′=OA,
A′就是点A关于直线l的对称点.
(3)连接A′B′,B′C′,C′A′,得到△A′B′C′即为所求
(2)同理分别画出点B,C关于直线l的对称点B′,C′
A
B
C
A′
B′
C′
O
作轴对称图形的方法
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
巩固练习
【例】如图所示,已知△ABC和直线MN.
请作△A1B1C1,
使△A1B1C1和△ABC关于直线MN对称.
解:如图所示
巩固练习
【例】如图所示,已知△ABC和直线MN.
请作△A1B1C1,
使△A1B1C1和△ABC关于直线MN对称.
解:如图所示,作法如下.
巩固练习
利用轴对称知识画图:
(1)作出图形AOCB关于直线a,b对称的图形,围成一个封闭图形;
(2)由(1)得到的星形图形中有_____条对称轴;
(3)用剪刀剪出这个星形图,正方形纸片需要对折___次.(只剪一刀)
4
3
解:(1)如图所示.
巩固练习
利用轴对称知识画图:
(1)作出图形AOCB关于直线a,b对称的图形,围成一个封闭图形;
(2)由(1)得到的星形图形中有_____条对称轴;
(3)用剪刀剪出这个星形图,正方形纸片需要对折___次.(只剪一刀)
4
3
解:(1)如图所示.
巩固练习
P68
T1.如图,把下列图形补成关于直线l的对称图形.
课堂小结
画轴对称图形
作图原理
作图方法
对称轴是对称点连线段的垂直平分线.
(1)找特征点;
(2)作垂线;
(3)截取等长;
(4)依次连线.
课堂小结
1.
成轴对称的两个图形中的任何一个都可以看作是___________________________得到的.
经过轴对称变换后的图形和原图形的_____、_____完全相同,连接任意一对对应点的线段都被对称轴__________.
2.
观察规律并填空:
.
3.
下列图形中,点P与P′关于直线MN对称的是(
)
另一个图形经过轴对称变换
大小
形状
垂直平分
D
课堂小结
4.
作已知点关于某直线的对称点的第一步是(
)
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
5.
下列各组图形中,其中一个图形能由另一个图形通过轴对称变换得到的是(
)
B
C
15
《学导练》P47-48
暗线本A:
P55
T5、P56
T11
请输入标题文字
《课堂小测本》P137
作业
