人教版上册八年级数学13.3.3 等边三角形性质与判定 课件(共17张PPT)
文档属性
| 名称 | 人教版上册八年级数学13.3.3 等边三角形性质与判定 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 302.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
第十三章
轴对称
13.3
等腰三角形
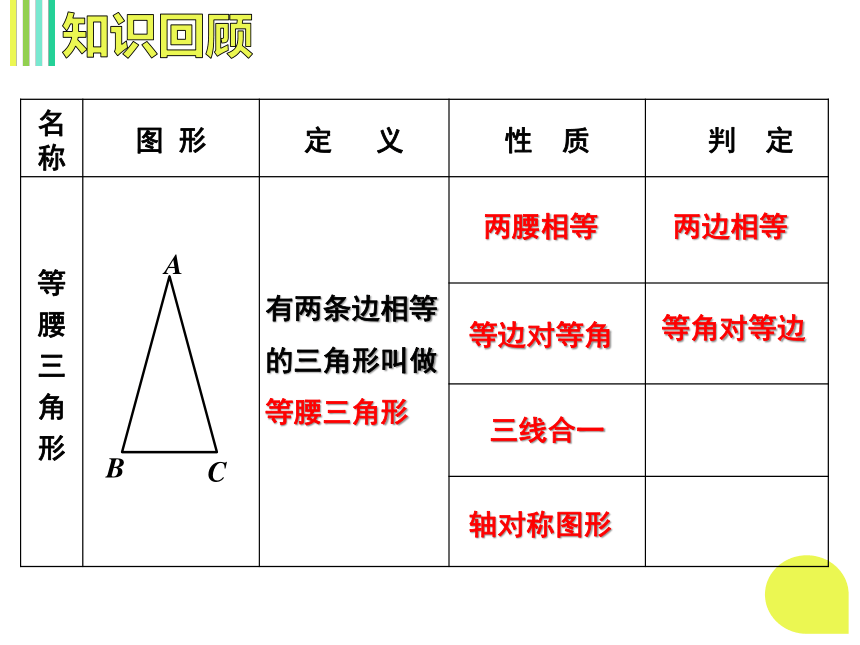
知识回顾
名称
图
形
定
义
性
质
判
定
等
腰
三
角
形
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
A
B
C
有两条边相等的三角形叫做等腰三角形
探究新知
等腰三角形
等边三角形
一般三角形
在等腰三角形中,有一种特殊的情况,就是底与腰相等,
即三角形的三边相等,我们把三条边都相等的三角形
叫作等边三角形.
探究新知
等边三角形的性质
A
B
C
A
B
C
问题1
等边三角形的三个内角之间有什么关系?
等腰三角形
∵AB=AC
∴∠B=∠C
等边三角形
∵AB=AC=BC
∵AB=AC
∴∠B=∠C
∵AC=BC
∴∠A=∠B
∴∠A=∠B=∠C
内角和为180°
=60°
探究新知
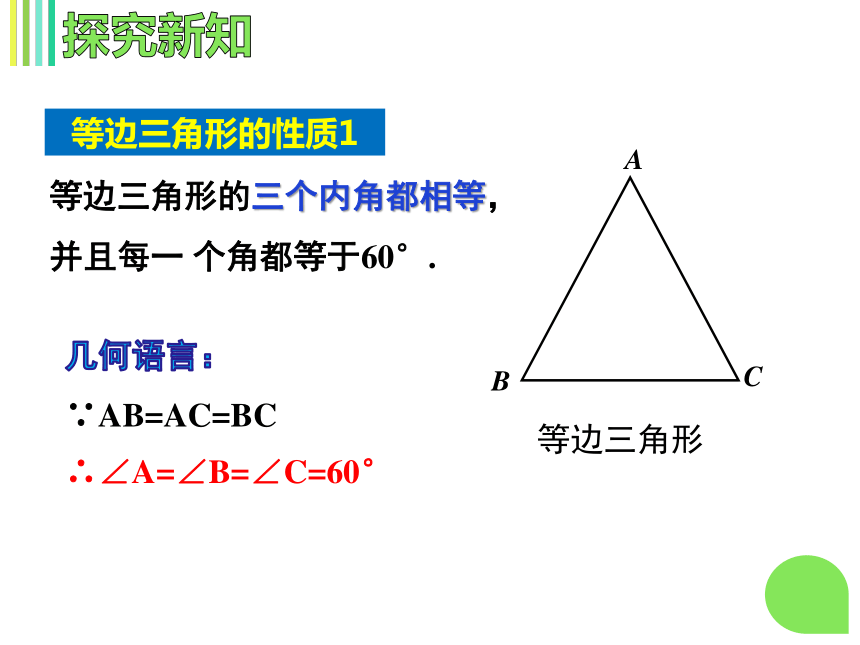
等边三角形的性质1
等边三角形的三个内角都相等,
并且每一
个角都等于60°.
A
B
C
等边三角形
几何语言:
∵AB=AC=BC
∴∠A=∠B=∠C=60°
探究新知
A
B
C
A
B
C
问题2
等边三角形有“三线合一”的性质吗?
等边三角形有几条对称轴?
等边三角形每条边上的中线,高
和所对角的平分线都“三线合一”.
顶角的平分线、底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
性质2
探究新知
图形
等腰三角形
性
质
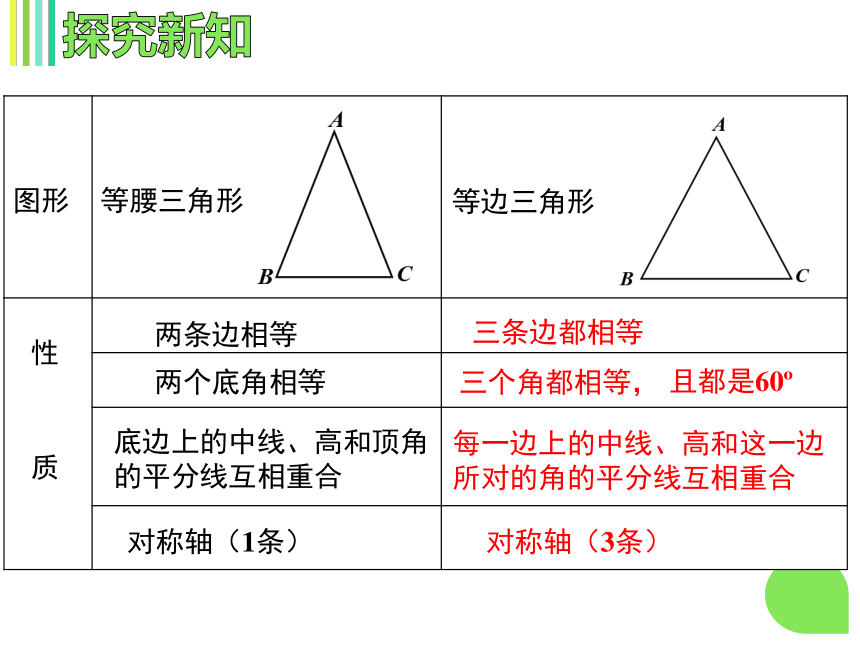
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60?
两条边相等
三条边都相等
探究新知
等边三角形的判定
图形
等腰三角形
判
定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?
等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.
巩固练习
辩一辩:根据条件判断下列三角形是否为等边三角形.
(1)
(2)
(6)
(5)
不
是
是
是
是
是
(4)
(3)
不一定
是
例题讲解
例4
如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.
证明:
∵
△ABC是等边三角形,
∴
∠A=
∠B=
∠C.
∵
DE//BC,
∴
∠ADE=
∠B,
∠
AED=
∠C.
∴
∠A=
∠ADE=
∠
AED.
∴
△ADE是等边三角形.
A
C
B
D
E
巩固练习
【例1】如图所示,已知等边△ABC中,D是AB上一点,∠EDF=60°,则∠AED=( )
A.
∠B
B.
∠BFD
C.
∠ADE
D.
∠BDF
D
1.下列三角形,其中是等边三角形的有( )
①有两个角等于60°;
②有一个角等于60°的等腰三角形;
③三个外角(每个顶点处各取一个外角)都相等的三角形;
④一腰上的中线也是这条腰上的高的等腰三角形.
A.
①②③ B.
①②④
C.
①③
D.
①②③④
D
60°
?
巩固练习
【例2】如图,等边△ABC中,点P在△ABC内,
点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明理由.
解:△APQ为等边三角形.
理由:∵△ABC为等边三角形,
∴AB=AC.
在△ABP和△ACQ中,
AB=AC,
∠ABP=∠ACQ,
BP=CQ,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°
∴∠PAQ=∠CAQ+∠PAC=60°.
∴△APQ是等边三角形.
巩固练习
2.如图,在△ABC中,点D是AB上的一点,且AD=DC=DB,∠B=30°.
求证:△ADC是等边三角形.
证明:∵∠B=30°,DC=DB,
∴∠DCB=∠B=30°,
∠ADC=2∠B=60°.
又∵AD=CD,
∴△ADC是等边三角形.
30°
30°
60°
课堂小结
等边
三角形
定义
底=腰
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60
°
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
三边法
三角法
等腰三角形法
课堂小结
1.
______________的三角形叫做等边三角形.
2.
等边三角形的三个内角都相等,
并且每一个角都等于_______.
3.
△ABC是等腰三角形,周长为15cm且∠A=60°,
则BC=_______cm.
三条边都相等
60°
5
课堂小结
4.
关于等边三角形,下列说法错误的是(
)
A.
等边三角形中,各边都相等
B.
等边三角形是特殊的等腰三角形
C.
三个角都等于60°的三角形是等边三角形
D.
有一个角为60°的等腰三角形不是等边三角形
D
5.等边△ABC两条角平分线BD和CE相交所夹锐角度数为( )
A.
60° B.
90°
C.
120°
D.
150°
A
17
《学导练》P59-60
预习P80-81
《学导练》P61
《课堂小测本》
P141-142
作业
明早交小组暗线本
第十三章
轴对称
13.3
等腰三角形
知识回顾
名称
图
形
定
义
性
质
判
定
等
腰
三
角
形
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
A
B
C
有两条边相等的三角形叫做等腰三角形
探究新知
等腰三角形
等边三角形
一般三角形
在等腰三角形中,有一种特殊的情况,就是底与腰相等,
即三角形的三边相等,我们把三条边都相等的三角形
叫作等边三角形.
探究新知
等边三角形的性质
A
B
C
A
B
C
问题1
等边三角形的三个内角之间有什么关系?
等腰三角形
∵AB=AC
∴∠B=∠C
等边三角形
∵AB=AC=BC
∵AB=AC
∴∠B=∠C
∵AC=BC
∴∠A=∠B
∴∠A=∠B=∠C
内角和为180°
=60°
探究新知
等边三角形的性质1
等边三角形的三个内角都相等,
并且每一
个角都等于60°.
A
B
C
等边三角形
几何语言:
∵AB=AC=BC
∴∠A=∠B=∠C=60°
探究新知
A
B
C
A
B
C
问题2
等边三角形有“三线合一”的性质吗?
等边三角形有几条对称轴?
等边三角形每条边上的中线,高
和所对角的平分线都“三线合一”.
顶角的平分线、底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
性质2
探究新知
图形
等腰三角形
性
质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60?
两条边相等
三条边都相等
探究新知
等边三角形的判定
图形
等腰三角形
判
定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?
等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.
巩固练习
辩一辩:根据条件判断下列三角形是否为等边三角形.
(1)
(2)
(6)
(5)
不
是
是
是
是
是
(4)
(3)
不一定
是
例题讲解
例4
如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.
证明:
∵
△ABC是等边三角形,
∴
∠A=
∠B=
∠C.
∵
DE//BC,
∴
∠ADE=
∠B,
∠
AED=
∠C.
∴
∠A=
∠ADE=
∠
AED.
∴
△ADE是等边三角形.
A
C
B
D
E
巩固练习
【例1】如图所示,已知等边△ABC中,D是AB上一点,∠EDF=60°,则∠AED=( )
A.
∠B
B.
∠BFD
C.
∠ADE
D.
∠BDF
D
1.下列三角形,其中是等边三角形的有( )
①有两个角等于60°;
②有一个角等于60°的等腰三角形;
③三个外角(每个顶点处各取一个外角)都相等的三角形;
④一腰上的中线也是这条腰上的高的等腰三角形.
A.
①②③ B.
①②④
C.
①③
D.
①②③④
D
60°
?
巩固练习
【例2】如图,等边△ABC中,点P在△ABC内,
点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明理由.
解:△APQ为等边三角形.
理由:∵△ABC为等边三角形,
∴AB=AC.
在△ABP和△ACQ中,
AB=AC,
∠ABP=∠ACQ,
BP=CQ,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°
∴∠PAQ=∠CAQ+∠PAC=60°.
∴△APQ是等边三角形.
巩固练习
2.如图,在△ABC中,点D是AB上的一点,且AD=DC=DB,∠B=30°.
求证:△ADC是等边三角形.
证明:∵∠B=30°,DC=DB,
∴∠DCB=∠B=30°,
∠ADC=2∠B=60°.
又∵AD=CD,
∴△ADC是等边三角形.
30°
30°
60°
课堂小结
等边
三角形
定义
底=腰
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60
°
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
三边法
三角法
等腰三角形法
课堂小结
1.
______________的三角形叫做等边三角形.
2.
等边三角形的三个内角都相等,
并且每一个角都等于_______.
3.
△ABC是等腰三角形,周长为15cm且∠A=60°,
则BC=_______cm.
三条边都相等
60°
5
课堂小结
4.
关于等边三角形,下列说法错误的是(
)
A.
等边三角形中,各边都相等
B.
等边三角形是特殊的等腰三角形
C.
三个角都等于60°的三角形是等边三角形
D.
有一个角为60°的等腰三角形不是等边三角形
D
5.等边△ABC两条角平分线BD和CE相交所夹锐角度数为( )
A.
60° B.
90°
C.
120°
D.
150°
A
17
《学导练》P59-60
预习P80-81
《学导练》P61
《课堂小测本》
P141-142
作业
明早交小组暗线本
