12.4分式方程(拓展)-冀教版八年级数学上册课件(共17张PPT)
文档属性
| 名称 | 12.4分式方程(拓展)-冀教版八年级数学上册课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 20:04:50 | ||
图片预览





文档简介
(共17张PPT)
12.4分式方程(拓展)
冀教版九上
第十二章
分式和分式方程
新课引入
新课学习
典例精析
测试小结
解决含有字母系数的分式方程问题
3.
解决分式方程有、无解的问题.
2.
解决分式方程值为正、负的问题.
1.
理解解分式方程会出现的三种情况.
学习目标
冀教版九上
新课引入
解下列方程(3名学生在黑板板演)
解:去分母,得
2x-6=5(x-3)
解得,x=3
检验:当x=3时,
x-3=0
∴x=3是原方程的増根
原分式方程无解
解:去分母,得
x+1+2=x-1
3=-1
∴整式方程无解
∴原分式方程无解
解:去分母,得
x+3=4x
解得,x=1
检验:当x=1时,
2x(x+3)≠0
∴x=1是原方程的根
思考:解分式方程的结果会有几种情况?
有增根
整式方程无解
整式方程有根
分母≠0
3.分式方程有解.
2.
分式方程所化的整式方程无解,原方程无解.
1.
分式方程有増根,原方程无解.
一、解分式方程会出现3种结果
新课学习
新课学习
二、分式方程有解、无解的条件
1.分式方程有解的条件
整式方程有解
分式方程分母≠0
2.分式方程无解的条件
整式方程无解
分式方程有増根
且
或
整式方程有解
分式方程分母=0
且
典例精析
例1.
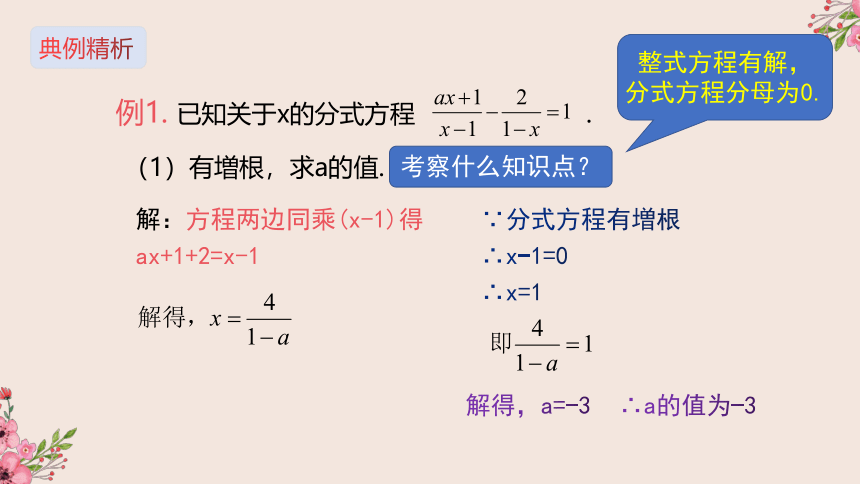
已知关于x的分式方程
.
(1)有増根,求a的值.
解:方程两边同乘(x-1)得
ax+1+2=x-1
∵分式方程有増根
∴x-1=0
∴x=1
解得,a=-3
∴a的值为-3
整式方程有解,分式方程分母为0.
考察什么知识点?
典例精析
例1.
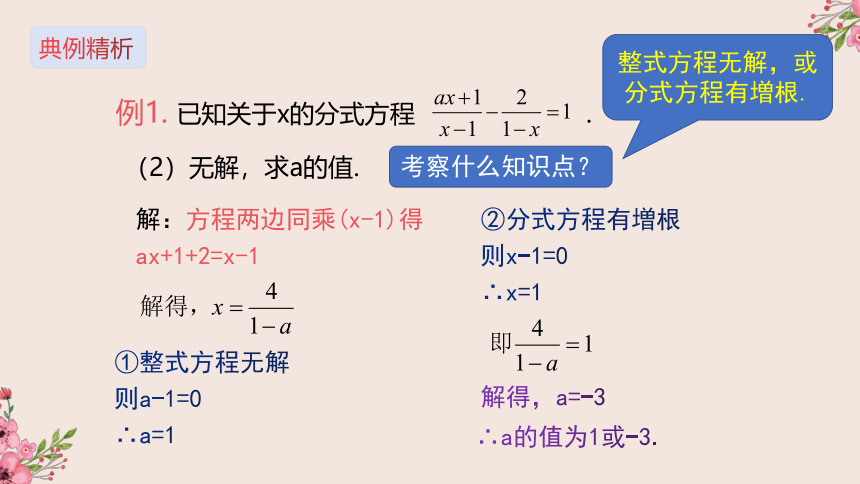
已知关于x的分式方程
.
(2)无解,求a的值.
解:方程两边同乘(x-1)得
ax+1+2=x-1
②分式方程有増根
则x-1=0
∴x=1
解得,a=-3
①整式方程无解
则a-1=0
∴a=1
∴a的值为1或-3.
考察什么知识点?
整式方程无解,或分式方程有増根.
典例精析
例1.
已知关于x的分式方程
.
(3)有解,求a的取值范围.
解:方程两边同乘(x-1)得
ax+1+2=x-1
②分式方程没有増根
则x-1≠0
∴x≠1
解得,a≠-3
①整式方程有解
则a-1≠0
∴a≠1
∴a的取值范围是a≠1且a≠-3.
考察什么知识点?
整式方程有解,且分式方程无増根.
典例精析
例1.
已知关于x的分式方程
.
(4)当a为何值时,方程的根为4.
解:方程两边同乘(x-1)得
ax+1+2=x-1
解得,a=0
经检验a=0是方程的根
把x=4代入,得
∴a为4时,方程的根为4.
这是一个分式方程,不要忘了检验哦.
典例精析
例1.
已知关于x的分式方程
.
(5)当a为何值时,方程的根为非负数.
解:方程两边同乘(x-1)得
ax+1+2=x-1
解得,a<1
∵x≥0
∴当a<1时,方程的根为非负数.
这样做对吗?
漏了什么条件?
不对,漏了隐含条件“方程有解”
典例精析
例1.
已知关于x的分式方程
.
(5)当a为何值时,方程的根为非负数.
解:方程两边同乘(x-1)得
ax+1+2=x-1
解得,a≠-3,a≠1,a<1
要保证分式方程有解
同时x≥0
∴当a<1且a≠-3时,方程的根为非负数.
知识点:方程有解且x≥0.
典例精析
例1.
已知关于x的分式方程
.
(6)当a为何值时,方程的根为负数.
解:方程两边同乘(x-1)得
ax+1+2=x-1
解得,a≠-3,a≠1,a>1
要保证分式方程有解
同时x<0
∴当a>1,方程的根为负数.
知识点:方程有解且x<0.
总结提升
三、分式方程的解为正或负时的条件
分式方程的解为正
分式方程有解
x>0
分式方程的解为负
分式方程有解
x<0
且
且
总结提升
四、解决含有字母系数的分式方程的有关问题
1.步骤:去分母,化为整式方程;
解出x;
根据题目要求,对x加限制条件,解决问题.
2.注意:看清题目要求,扣准知识点;
做解为正、负时,要注意隐含条件“方程有解”
课堂小测
已知关于x的分式方程
(3)若方程的解为负数,则_____________.
(2)若方程无解,则___________________.
(1)若方程有増根,则______________.
m=-6或m=1.5
m=-6或m=1.5或m=-1
m>-1且m≠1.5
回顾小结
一、分式方程的结果
二、解决含有字母系数的分式方程的有关问题.
有解
整式方程有解且分式方程无増根
无解
整式方程无解或分式方程有増根
解为正或负
整式方程有解同时x>0(或x<0)
一般要先化为整式方程,并求出x.
同学们再见
12.4分式方程(拓展)
冀教版九上
第十二章
分式和分式方程
新课引入
新课学习
典例精析
测试小结
解决含有字母系数的分式方程问题
3.
解决分式方程有、无解的问题.
2.
解决分式方程值为正、负的问题.
1.
理解解分式方程会出现的三种情况.
学习目标
冀教版九上
新课引入
解下列方程(3名学生在黑板板演)
解:去分母,得
2x-6=5(x-3)
解得,x=3
检验:当x=3时,
x-3=0
∴x=3是原方程的増根
原分式方程无解
解:去分母,得
x+1+2=x-1
3=-1
∴整式方程无解
∴原分式方程无解
解:去分母,得
x+3=4x
解得,x=1
检验:当x=1时,
2x(x+3)≠0
∴x=1是原方程的根
思考:解分式方程的结果会有几种情况?
有增根
整式方程无解
整式方程有根
分母≠0
3.分式方程有解.
2.
分式方程所化的整式方程无解,原方程无解.
1.
分式方程有増根,原方程无解.
一、解分式方程会出现3种结果
新课学习
新课学习
二、分式方程有解、无解的条件
1.分式方程有解的条件
整式方程有解
分式方程分母≠0
2.分式方程无解的条件
整式方程无解
分式方程有増根
且
或
整式方程有解
分式方程分母=0
且
典例精析
例1.
已知关于x的分式方程
.
(1)有増根,求a的值.
解:方程两边同乘(x-1)得
ax+1+2=x-1
∵分式方程有増根
∴x-1=0
∴x=1
解得,a=-3
∴a的值为-3
整式方程有解,分式方程分母为0.
考察什么知识点?
典例精析
例1.
已知关于x的分式方程
.
(2)无解,求a的值.
解:方程两边同乘(x-1)得
ax+1+2=x-1
②分式方程有増根
则x-1=0
∴x=1
解得,a=-3
①整式方程无解
则a-1=0
∴a=1
∴a的值为1或-3.
考察什么知识点?
整式方程无解,或分式方程有増根.
典例精析
例1.
已知关于x的分式方程
.
(3)有解,求a的取值范围.
解:方程两边同乘(x-1)得
ax+1+2=x-1
②分式方程没有増根
则x-1≠0
∴x≠1
解得,a≠-3
①整式方程有解
则a-1≠0
∴a≠1
∴a的取值范围是a≠1且a≠-3.
考察什么知识点?
整式方程有解,且分式方程无増根.
典例精析
例1.
已知关于x的分式方程
.
(4)当a为何值时,方程的根为4.
解:方程两边同乘(x-1)得
ax+1+2=x-1
解得,a=0
经检验a=0是方程的根
把x=4代入,得
∴a为4时,方程的根为4.
这是一个分式方程,不要忘了检验哦.
典例精析
例1.
已知关于x的分式方程
.
(5)当a为何值时,方程的根为非负数.
解:方程两边同乘(x-1)得
ax+1+2=x-1
解得,a<1
∵x≥0
∴当a<1时,方程的根为非负数.
这样做对吗?
漏了什么条件?
不对,漏了隐含条件“方程有解”
典例精析
例1.
已知关于x的分式方程
.
(5)当a为何值时,方程的根为非负数.
解:方程两边同乘(x-1)得
ax+1+2=x-1
解得,a≠-3,a≠1,a<1
要保证分式方程有解
同时x≥0
∴当a<1且a≠-3时,方程的根为非负数.
知识点:方程有解且x≥0.
典例精析
例1.
已知关于x的分式方程
.
(6)当a为何值时,方程的根为负数.
解:方程两边同乘(x-1)得
ax+1+2=x-1
解得,a≠-3,a≠1,a>1
要保证分式方程有解
同时x<0
∴当a>1,方程的根为负数.
知识点:方程有解且x<0.
总结提升
三、分式方程的解为正或负时的条件
分式方程的解为正
分式方程有解
x>0
分式方程的解为负
分式方程有解
x<0
且
且
总结提升
四、解决含有字母系数的分式方程的有关问题
1.步骤:去分母,化为整式方程;
解出x;
根据题目要求,对x加限制条件,解决问题.
2.注意:看清题目要求,扣准知识点;
做解为正、负时,要注意隐含条件“方程有解”
课堂小测
已知关于x的分式方程
(3)若方程的解为负数,则_____________.
(2)若方程无解,则___________________.
(1)若方程有増根,则______________.
m=-6或m=1.5
m=-6或m=1.5或m=-1
m>-1且m≠1.5
回顾小结
一、分式方程的结果
二、解决含有字母系数的分式方程的有关问题.
有解
整式方程有解且分式方程无増根
无解
整式方程无解或分式方程有増根
解为正或负
整式方程有解同时x>0(或x<0)
一般要先化为整式方程,并求出x.
同学们再见
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
