冀教版八年级数学上册12.4分式方程课件(共22张PPT)
文档属性
| 名称 | 冀教版八年级数学上册12.4分式方程课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
12.4分式方程
冀教版九上
第十二章
分式和分式方程
新课引入
新课学习
典例精析
测试小结
3.
会解分式方程,会检验根的合理性.
2.
了解分式方程、分式方程的解、分式方程的増根.
1.
经历从实际问题中建立分式方程的过程.
学习目标
冀教版九上
新课引入
小明
小红
小明,你家离学校有多远?
那我要考考你了,我每天骑自行车到学校,每小时骑15km可早到10分钟,每小时骑12km,就会迟到5分钟,你知道我家离学校多远了吗?
新课引入
小明
小红
对,你答对了.
新课引入
小明
小红
哦......
我要想一想...
我也要考你一下:我家距离学校38km,我每天先乘公共汽车,再步行2km到校,共用时间1h,公共汽车的速度是我的9倍,你能算出我步行的速度吗?
新课引入
我们来帮一帮小明吧
(1)题目中的数量关系有哪些?
①公共汽车的速度=9×步行速度
②乘公共汽车的时间+步行时间=1
(2)设未知数,列出方程.
新课引入
设小红步行的时间为xh,可得方程
当用“①公共汽车的速度=9×步行速度”做数量关系时
当用“②乘公共汽车的时间+步行时间=1”做数量关系时
设小红步行的速度为xkm/h,可得方程
一般作为数量关系的量与作未知数的量是不同的量.
新课学习
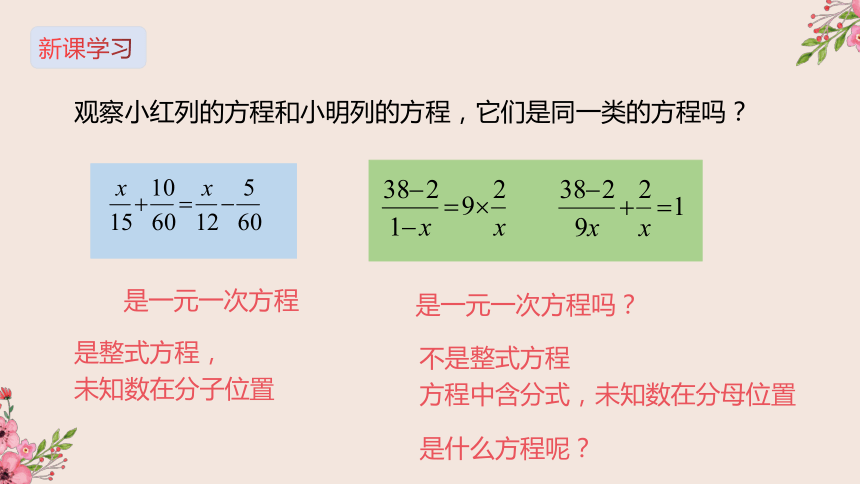
观察小红列的方程和小明列的方程,它们是同一类的方程吗?
是一元一次方程吗?
是一元一次方程
不是整式方程
方程中含分式,未知数在分母位置
是整式方程,
未知数在分子位置
是什么方程呢?
新课学习
一、分式方程的概念
注意关键点
未知数在分母位置
像
这样,
分母中含有未知数的方程,叫做分式方程.
课堂小练
练一练:判断下列方程是不是分式方程?
(4)x
2
+
-2x
+
1
=
0
(5)4x=5
√
×
√
×
×
新课学习
二、分式方程的根
使得分式方程等号两端相等的未知数的值叫做分式方程的解.(也叫做分式方程的根)
A.
x=1
B.
x=2
B.
x=3
D.
x=4.
C
1
常用把根代入的方法
新课学习
三、解分式方程
例1.我们来试着解小明列出的两个分式方程
分析:根据解一元一次方程的经验
①解方程时,遇到分母先去分母;
②去分母时,类比一元一次方程的去分母,可找分母的最简公分母;
③找最简公分母的方法,与分式通分时相同.
新课学习
解:方程两边同乘x(1-x),得
36x=18(1-x)
解得
,
检验:当
时,
左边=54,右边=54
左边=右边
解:方程两边同乘9x,得
36+18=9x
解得
,x=6
检验:当x=6时,
左边=54,右边=54
左边=右边
新课学习
解方程
.在解的过程中,说说你有什么发现?
解:原方程可化为
方程两边同乘(x-1)得
x+1=-(x-3)+(x-1)
解得,x=1
检验:当x=1时,
方程的左、右两边均无意义.
①当分母通过提负号可以变为相同是,要先变再去分母
②去分母时,单独的整数(如:1)也要乘公分母
③x的取值使方程没有意义,x=1不是分式方程的根
増根
新课学习
四、分式方程的増根
在解分式方程时,通过去分母将分式方程转化为整式方程,并解这个整式方程,当将整式方程的根代入分式方程时,分母等于0,分式方程无解,我们把这样的根叫做分式方程的増根.
总结:分式増根的条件
①是整式方程的根;
②使分式方程的分母(或公分母)为0
.
总结提升
总结:
1.由于解分式方程时,可能产生増根,因此解分式方程必须检验.
2.
检验的方法是:将整式方程的根代入最简公分母中,若公分母≠0,则整式方程的根就是分式方程的根;若公分母=0,则整式方程的根就是分式方程的増根,分式方程无解.
典例精析
例1.
解下列方程
解:原方程可化为
方程两边同乘(x-3)得
1=2(x-3)-x
解得,x=7
检验:当x=7时,x-3≠0
∴x=7是原方程的根.
将分母调换成相同
方法:提负号
去分母
方法:同乘最简公分母
解整式方程
检验
方法:代入公分母
解分式方程的步骤:
1化
2去
3解
4验
典例精析
例1.
解下列方程
解:原方程可化为
方程两边同乘(x+2)(x-2)得
4(x+2)=16-3(x-2)
解得,x=2
检验:当x=2时,(+2)(x-2)=0
∴x=2是原方程的増根
原方程无解.
当分母可以分解因式时,宜先分解因式
课堂小练
解下列分式方程.(写到练习本上,步骤要规范哦)
x=-1
x=7
是原方程的増根
典例精析
分析:増根的条件是①是整式方程的根,②使分式方程的分母等于0.则x-3=0,x=3;同时x=3是整式方程的根,应将x=3代入整式方程.
例2.若关于x的方程
有増根,求m
的值
.
解:方程两边同乘(x-3),得
2-(x-3)=m
解得,x=5-m
∵分式方程有増根
∴x-3=0
∴x=3
把x=3代入
x=5-m,得
3=5-m
∴m=2
课堂小测
1.下列方程是分式方程的是(
)
B
课堂小测
B
2.解分式方程
时,去分母可得(
)
回顾小结
一、分式方程的概念.
分母中含有未知数的方程,叫做分式方程.
二、分式方程的根.
三、分式方程的増根.
①是整式方程的根;②使公分母为0.
使分式方程左右两边相等的未知数的值,叫做分式方程的根.
四、解分式方程的步骤.
1化、2去、3解、4验
同学们再见
12.4分式方程
冀教版九上
第十二章
分式和分式方程
新课引入
新课学习
典例精析
测试小结
3.
会解分式方程,会检验根的合理性.
2.
了解分式方程、分式方程的解、分式方程的増根.
1.
经历从实际问题中建立分式方程的过程.
学习目标
冀教版九上
新课引入
小明
小红
小明,你家离学校有多远?
那我要考考你了,我每天骑自行车到学校,每小时骑15km可早到10分钟,每小时骑12km,就会迟到5分钟,你知道我家离学校多远了吗?
新课引入
小明
小红
对,你答对了.
新课引入
小明
小红
哦......
我要想一想...
我也要考你一下:我家距离学校38km,我每天先乘公共汽车,再步行2km到校,共用时间1h,公共汽车的速度是我的9倍,你能算出我步行的速度吗?
新课引入
我们来帮一帮小明吧
(1)题目中的数量关系有哪些?
①公共汽车的速度=9×步行速度
②乘公共汽车的时间+步行时间=1
(2)设未知数,列出方程.
新课引入
设小红步行的时间为xh,可得方程
当用“①公共汽车的速度=9×步行速度”做数量关系时
当用“②乘公共汽车的时间+步行时间=1”做数量关系时
设小红步行的速度为xkm/h,可得方程
一般作为数量关系的量与作未知数的量是不同的量.
新课学习
观察小红列的方程和小明列的方程,它们是同一类的方程吗?
是一元一次方程吗?
是一元一次方程
不是整式方程
方程中含分式,未知数在分母位置
是整式方程,
未知数在分子位置
是什么方程呢?
新课学习
一、分式方程的概念
注意关键点
未知数在分母位置
像
这样,
分母中含有未知数的方程,叫做分式方程.
课堂小练
练一练:判断下列方程是不是分式方程?
(4)x
2
+
-2x
+
1
=
0
(5)4x=5
√
×
√
×
×
新课学习
二、分式方程的根
使得分式方程等号两端相等的未知数的值叫做分式方程的解.(也叫做分式方程的根)
A.
x=1
B.
x=2
B.
x=3
D.
x=4.
C
1
常用把根代入的方法
新课学习
三、解分式方程
例1.我们来试着解小明列出的两个分式方程
分析:根据解一元一次方程的经验
①解方程时,遇到分母先去分母;
②去分母时,类比一元一次方程的去分母,可找分母的最简公分母;
③找最简公分母的方法,与分式通分时相同.
新课学习
解:方程两边同乘x(1-x),得
36x=18(1-x)
解得
,
检验:当
时,
左边=54,右边=54
左边=右边
解:方程两边同乘9x,得
36+18=9x
解得
,x=6
检验:当x=6时,
左边=54,右边=54
左边=右边
新课学习
解方程
.在解的过程中,说说你有什么发现?
解:原方程可化为
方程两边同乘(x-1)得
x+1=-(x-3)+(x-1)
解得,x=1
检验:当x=1时,
方程的左、右两边均无意义.
①当分母通过提负号可以变为相同是,要先变再去分母
②去分母时,单独的整数(如:1)也要乘公分母
③x的取值使方程没有意义,x=1不是分式方程的根
増根
新课学习
四、分式方程的増根
在解分式方程时,通过去分母将分式方程转化为整式方程,并解这个整式方程,当将整式方程的根代入分式方程时,分母等于0,分式方程无解,我们把这样的根叫做分式方程的増根.
总结:分式増根的条件
①是整式方程的根;
②使分式方程的分母(或公分母)为0
.
总结提升
总结:
1.由于解分式方程时,可能产生増根,因此解分式方程必须检验.
2.
检验的方法是:将整式方程的根代入最简公分母中,若公分母≠0,则整式方程的根就是分式方程的根;若公分母=0,则整式方程的根就是分式方程的増根,分式方程无解.
典例精析
例1.
解下列方程
解:原方程可化为
方程两边同乘(x-3)得
1=2(x-3)-x
解得,x=7
检验:当x=7时,x-3≠0
∴x=7是原方程的根.
将分母调换成相同
方法:提负号
去分母
方法:同乘最简公分母
解整式方程
检验
方法:代入公分母
解分式方程的步骤:
1化
2去
3解
4验
典例精析
例1.
解下列方程
解:原方程可化为
方程两边同乘(x+2)(x-2)得
4(x+2)=16-3(x-2)
解得,x=2
检验:当x=2时,(+2)(x-2)=0
∴x=2是原方程的増根
原方程无解.
当分母可以分解因式时,宜先分解因式
课堂小练
解下列分式方程.(写到练习本上,步骤要规范哦)
x=-1
x=7
是原方程的増根
典例精析
分析:増根的条件是①是整式方程的根,②使分式方程的分母等于0.则x-3=0,x=3;同时x=3是整式方程的根,应将x=3代入整式方程.
例2.若关于x的方程
有増根,求m
的值
.
解:方程两边同乘(x-3),得
2-(x-3)=m
解得,x=5-m
∵分式方程有増根
∴x-3=0
∴x=3
把x=3代入
x=5-m,得
3=5-m
∴m=2
课堂小测
1.下列方程是分式方程的是(
)
B
课堂小测
B
2.解分式方程
时,去分母可得(
)
回顾小结
一、分式方程的概念.
分母中含有未知数的方程,叫做分式方程.
二、分式方程的根.
三、分式方程的増根.
①是整式方程的根;②使公分母为0.
使分式方程左右两边相等的未知数的值,叫做分式方程的根.
四、解分式方程的步骤.
1化、2去、3解、4验
同学们再见
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
