北师大版数学七年级上册3.5 探索与表达规律课件(第1课时 26张)
文档属性
| 名称 | 北师大版数学七年级上册3.5 探索与表达规律课件(第1课时 26张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 779.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 00:00:00 | ||
图片预览





文档简介
3.5 探索与表达规律(第1课时)
导入新知
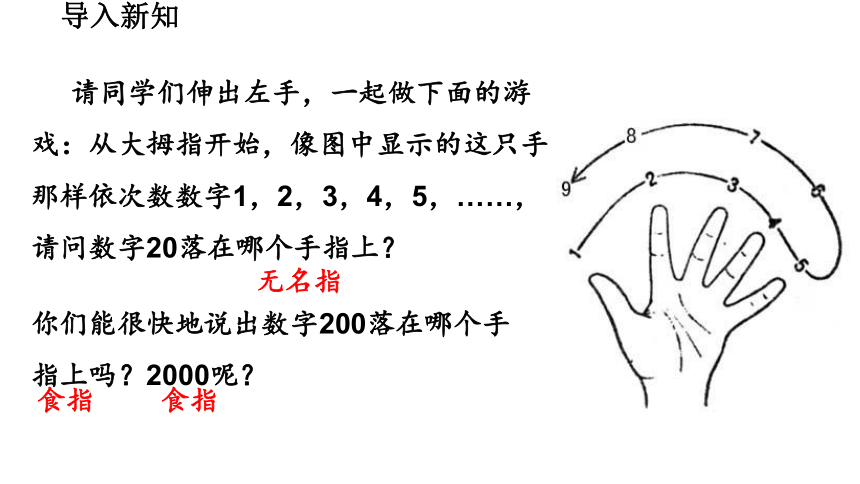
请同学们伸出左手,一起做下面的游戏:从大拇指开始,像图中显示的这只手那样依次数数字1,2,3,4,5,……,请问数字20落在哪个手指上?
你们能很快地说出数字200落在哪个手指上吗?2000呢?
无名指
食指
食指
素养目标
1.观察日历中3×3方框里九个数之间的关系,发现规律,并用代数式表示规律.
2.用合并同类项和去括号法则验证规律.
3.能运用所总结的规律解决问题.
探究新知
知识点 1
数字变化中的规律
观察下图日历,请你回答以下问题:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(2)竖列三个数也有这种关系吗?
(1)日历中横排三个数(如9、10、11)相加的和与中间的数字(10)有什么关系?
答:横排三个数相加的和是中间数字的3倍.
答:是的.
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
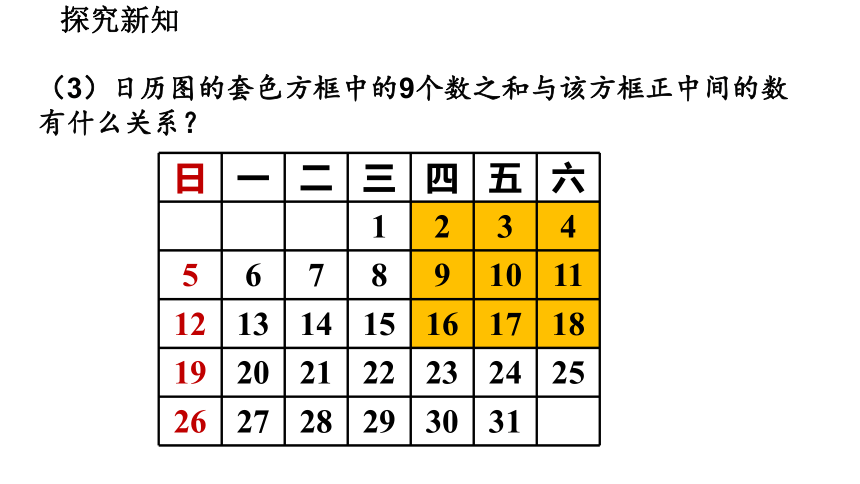
(3)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系?
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}2
3
4
9
10
11
16
17
18
答:因为 (2+18)+(3+17)+(4+16)+(9+11)+10=90,
10×9=90,
所以这9个数的和等于正中间的数的9倍.
探究新知
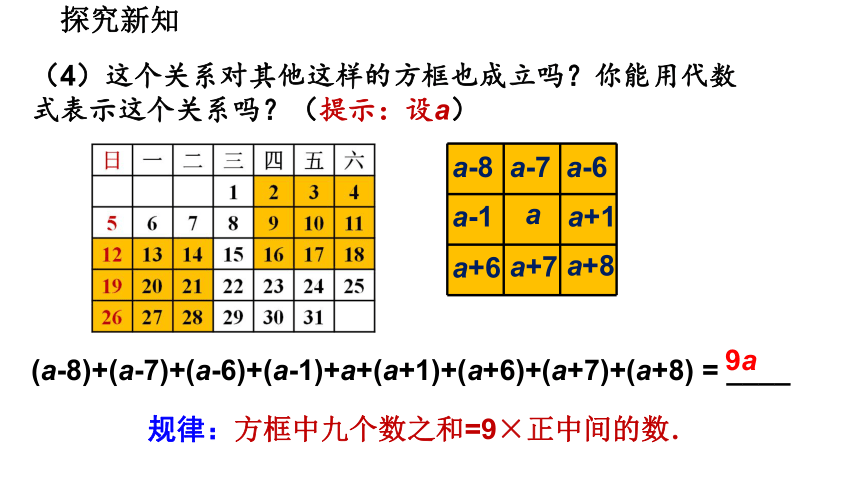
(4)这个关系对其他这样的方框也成立吗?你能用代数式表示这个关系吗?(提示:设a)
(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)+(a+7)+(a+8) = ____
规律:方框中九个数之和=9×正中间的数.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
a
a-1
a-8
a-7
a-6
a+1
a+6
a+7
a+8
9a
探究新知
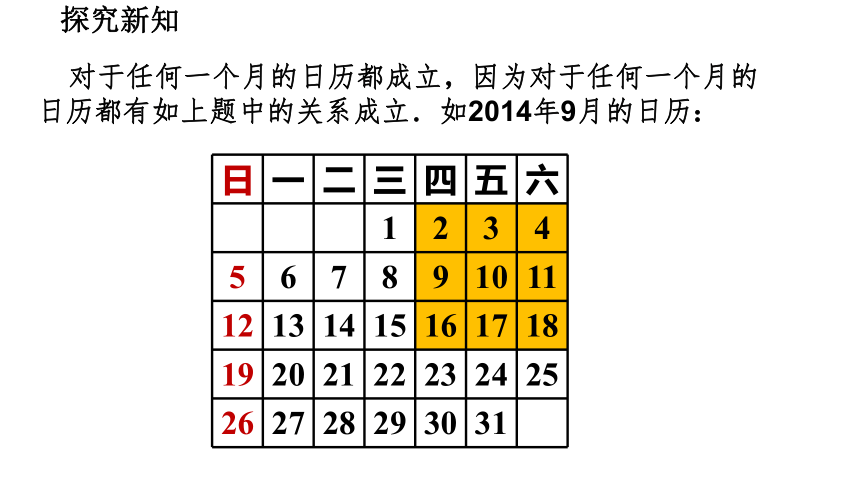
对于任何一个月的日历都成立,因为对于任何一个月的日历都有如上题中的关系成立.如2014年9月的日历:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
探究新知
如果将方框改为“H” 形框,你能发现哪些规律?如果改成十字形框呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
练一练
规律:“H”形中七数之和=7×中间数.
“H”形中七数之和=10+12+17+18+19+24+26
=126.
7×中间数=7×18=126.
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
规律: 十字形中五数之和=5×中间数.
十字形中五数之和
5×中间数
=70
=7+13+14+15+21
=70
=5 ×14
例 若按下图方式摆放桌子和椅子:
探究新知
素养考点
探索图形变化的规律
填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}桌子张数
1
2
3
4
5
…
n
可坐人数
…
6
10
8
14
12
2n+4
探究新知
餐桌的摆法二:
若按照上图的摆法摆放餐桌和凳子,完成下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}桌子张数
1
2
3
4
5
…
n
可坐人数
…
6
14
10
22
18
4n+2
探究新知
探索:若你是一家餐厅的大堂经理,由你负责在一个宽敞明亮的大厅里组织一次规模盛大的西式冷餐会,你会选择上面哪种餐桌的摆法?
提问:在桌数相同时,哪一种摆法容纳的人数更多?
答:第二种摆法容纳的人数更多.
答:选择第二种摆法.
方法点拨:规律探究问题的特点是问题的结论不是直接给出,而是通过对问题的观察、分析、归纳、概括、演算、判断等一系列的探究活动,方能得到问题的结论,这类问题,具有独特的规律性和探究性.
巩固练习
变式训练
如下列各图是用“ ”按一定规律排列而成的图案,第1个图案由4个“ ”组成,第2个图案由7个“ ”组成,第3个图案由10“ ”组成,……,则第n(n是正整数)个图案中由_____个“ ”组成.
3n+1
……
连接中考
(2019·黑龙江省中考真题)归纳“T ”字形,用棋子摆成的“T ”字形如图所示,按照图①,图②,图③的规律摆下去,摆成第n个“T ”字形需要的棋子个数为_______.
3n+2.
课堂检测
基础巩固题
A
1.用棋子摆出下列一组“口”字,按照这种方法摆下去,则摆第n个“口”字需用棋子( )
A.4n枚 B.(4n-4)枚
C.(4n+4)枚 D.n2 枚
课堂检测
基础巩固题
2.用正方形套住日历中的任意 9 个数,若中间的数是 14,则这 9 个数的和是______.
126
课堂检测
基础巩固题
3. 如图是在正方形网格中按规律填成的阴影,根据此规律,第n个图中的阴影部分小正方形的个数是_____________.
????(????+????)+?????
?
课堂检测
基础巩固题
n(n+1)
4.如图,图①有2个相同的小长方形,图②有6个相同的小长方形,图③有12个相同的小长方形,图④有20个相同的小长方形……按此规律,那么图n有__________个相同的小长方形.
课堂检测
基础巩固题
5.假设有足够多的黑白围棋子,它们按照一定的规律排成一行,
如图:
○○●●○●○○●●○●○○●●○●○○●●○●……
那么请问第2 017个棋子是黑的还是白的?
白的.
能力提升题
课堂检测
观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,……按此规律,图形⑧中星星的颗数是( )
A.43 B. 45 C.51 D.53
C
拓广探索题
课堂检测
先观察,再解答:图①是生活中常见的日历,你对它了解吗?
课堂检测
(1)图②是另一个月的日历,a表示该月中某一天,b,c,d是该月中其他3天,b,c,d与a分别有什么关系(用含a的代数式表示)?
解:b=a-7,c=a+1,d=a+5.
课堂检测
(2)用一个长方形框圈出日历中的三个数字(图②中的阴影部分),如果这三个数字之和为51,那么这三个数各是多少?
解:设长方形框圈出日历中的中间的数字为a,
则上边的数字为a-7,下边的数字为a+7.
因为3a=51,所以a=17.
所以它们的和为a+a-7+a+7=3a.
所以这三个数各是10,17,24.
课堂检测
(3)第(2)小题中圈出的三个数字的和可能是64吗?为什么?
解:由题意知,3a=64,解得a=????????????.
?
所以圈出的三个数字的和不可能是64.
因为????????????不是整数,
?
探索数字与图形规律
探索规律的一般方法
规律探索体现了从特殊到一般,再从一般到特殊的数学思想
课堂小结
观察
猜想
归纳
验证
导入新知
请同学们伸出左手,一起做下面的游戏:从大拇指开始,像图中显示的这只手那样依次数数字1,2,3,4,5,……,请问数字20落在哪个手指上?
你们能很快地说出数字200落在哪个手指上吗?2000呢?
无名指
食指
食指
素养目标
1.观察日历中3×3方框里九个数之间的关系,发现规律,并用代数式表示规律.
2.用合并同类项和去括号法则验证规律.
3.能运用所总结的规律解决问题.
探究新知
知识点 1
数字变化中的规律
观察下图日历,请你回答以下问题:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(2)竖列三个数也有这种关系吗?
(1)日历中横排三个数(如9、10、11)相加的和与中间的数字(10)有什么关系?
答:横排三个数相加的和是中间数字的3倍.
答:是的.
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(3)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系?
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}2
3
4
9
10
11
16
17
18
答:因为 (2+18)+(3+17)+(4+16)+(9+11)+10=90,
10×9=90,
所以这9个数的和等于正中间的数的9倍.
探究新知
(4)这个关系对其他这样的方框也成立吗?你能用代数式表示这个关系吗?(提示:设a)
(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)+(a+7)+(a+8) = ____
规律:方框中九个数之和=9×正中间的数.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
a
a-1
a-8
a-7
a-6
a+1
a+6
a+7
a+8
9a
探究新知
对于任何一个月的日历都成立,因为对于任何一个月的日历都有如上题中的关系成立.如2014年9月的日历:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
探究新知
如果将方框改为“H” 形框,你能发现哪些规律?如果改成十字形框呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
练一练
规律:“H”形中七数之和=7×中间数.
“H”形中七数之和=10+12+17+18+19+24+26
=126.
7×中间数=7×18=126.
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
规律: 十字形中五数之和=5×中间数.
十字形中五数之和
5×中间数
=70
=7+13+14+15+21
=70
=5 ×14
例 若按下图方式摆放桌子和椅子:
探究新知
素养考点
探索图形变化的规律
填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}桌子张数
1
2
3
4
5
…
n
可坐人数
…
6
10
8
14
12
2n+4
探究新知
餐桌的摆法二:
若按照上图的摆法摆放餐桌和凳子,完成下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}桌子张数
1
2
3
4
5
…
n
可坐人数
…
6
14
10
22
18
4n+2
探究新知
探索:若你是一家餐厅的大堂经理,由你负责在一个宽敞明亮的大厅里组织一次规模盛大的西式冷餐会,你会选择上面哪种餐桌的摆法?
提问:在桌数相同时,哪一种摆法容纳的人数更多?
答:第二种摆法容纳的人数更多.
答:选择第二种摆法.
方法点拨:规律探究问题的特点是问题的结论不是直接给出,而是通过对问题的观察、分析、归纳、概括、演算、判断等一系列的探究活动,方能得到问题的结论,这类问题,具有独特的规律性和探究性.
巩固练习
变式训练
如下列各图是用“ ”按一定规律排列而成的图案,第1个图案由4个“ ”组成,第2个图案由7个“ ”组成,第3个图案由10“ ”组成,……,则第n(n是正整数)个图案中由_____个“ ”组成.
3n+1
……
连接中考
(2019·黑龙江省中考真题)归纳“T ”字形,用棋子摆成的“T ”字形如图所示,按照图①,图②,图③的规律摆下去,摆成第n个“T ”字形需要的棋子个数为_______.
3n+2.
课堂检测
基础巩固题
A
1.用棋子摆出下列一组“口”字,按照这种方法摆下去,则摆第n个“口”字需用棋子( )
A.4n枚 B.(4n-4)枚
C.(4n+4)枚 D.n2 枚
课堂检测
基础巩固题
2.用正方形套住日历中的任意 9 个数,若中间的数是 14,则这 9 个数的和是______.
126
课堂检测
基础巩固题
3. 如图是在正方形网格中按规律填成的阴影,根据此规律,第n个图中的阴影部分小正方形的个数是_____________.
????(????+????)+?????
?
课堂检测
基础巩固题
n(n+1)
4.如图,图①有2个相同的小长方形,图②有6个相同的小长方形,图③有12个相同的小长方形,图④有20个相同的小长方形……按此规律,那么图n有__________个相同的小长方形.
课堂检测
基础巩固题
5.假设有足够多的黑白围棋子,它们按照一定的规律排成一行,
如图:
○○●●○●○○●●○●○○●●○●○○●●○●……
那么请问第2 017个棋子是黑的还是白的?
白的.
能力提升题
课堂检测
观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,……按此规律,图形⑧中星星的颗数是( )
A.43 B. 45 C.51 D.53
C
拓广探索题
课堂检测
先观察,再解答:图①是生活中常见的日历,你对它了解吗?
课堂检测
(1)图②是另一个月的日历,a表示该月中某一天,b,c,d是该月中其他3天,b,c,d与a分别有什么关系(用含a的代数式表示)?
解:b=a-7,c=a+1,d=a+5.
课堂检测
(2)用一个长方形框圈出日历中的三个数字(图②中的阴影部分),如果这三个数字之和为51,那么这三个数各是多少?
解:设长方形框圈出日历中的中间的数字为a,
则上边的数字为a-7,下边的数字为a+7.
因为3a=51,所以a=17.
所以它们的和为a+a-7+a+7=3a.
所以这三个数各是10,17,24.
课堂检测
(3)第(2)小题中圈出的三个数字的和可能是64吗?为什么?
解:由题意知,3a=64,解得a=????????????.
?
所以圈出的三个数字的和不可能是64.
因为????????????不是整数,
?
探索数字与图形规律
探索规律的一般方法
规律探索体现了从特殊到一般,再从一般到特殊的数学思想
课堂小结
观察
猜想
归纳
验证
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
