26.3解直角三角形-冀教版九年级数学上册课件(共27张PPT)
文档属性
| 名称 | 26.3解直角三角形-冀教版九年级数学上册课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 22:43:24 | ||
图片预览






文档简介
(共27张PPT)
26.3
解直角三角形
冀教版九上
第二十六
解直角三角形
新课引入
新课学习
典例精析
测试小结
学
习
目
标
冀教版九上
1.梳理、归纳直角三角形章三边、两锐角、边角之间的关系.
2.选择恰当的直角三角形中三边、两锐角、边角之间的关系,解直角三角形.
3.体会解直角三角形的过程,规范解题格式.
创设情境,引入新课
解下列方程或方程组:
x=2
(1)2x=4
{
(2)
x-y=4
x+y=0
(3)
a=3
a+b=0
a+b+c=-1
{
x=2.y=-2
a=3,b=-3,c=-1.
怎样理解解方程中的“解”?
就是将方程中所有未知的数求出.
创设情境,引入新课
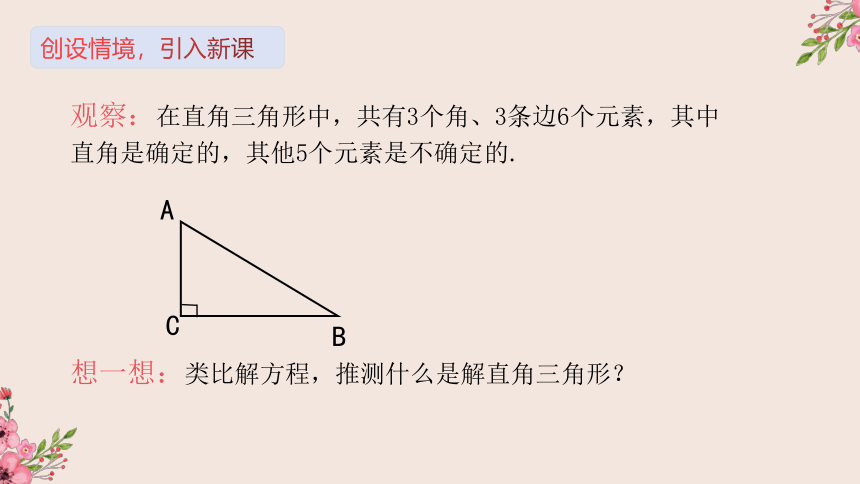
观察:在直角三角形中,共有3个角、3条边6个元素,其中直角是确定的,其他5个元素是不确定的.
想一想:类比解方程,推测什么是解直角三角形?
C
A
B
新课学习,探求未知
B
C
A
一、解直角三角形
在直角三角形中,除直角外,还有三条边和两个锐角共五个元素.由这五个元素中的已知元素求出其余未知元素的过程,叫做解直角三角形.
新课学习,探求未知
2.直角三角形中,未知的5个元素之间的关系
①三边之间的关系
B
C
A
c
b
a
已知任意两边可求出第三边
新课学习,探求未知
2.直角三角形中,未知的5个元素之间的关系
②两个锐角之间的关系
B
C
A
c
b
a
已知一个锐角可求出另一个锐角
新课学习,探求未知
2.直角三角形中,未知的5个元素之间的关系
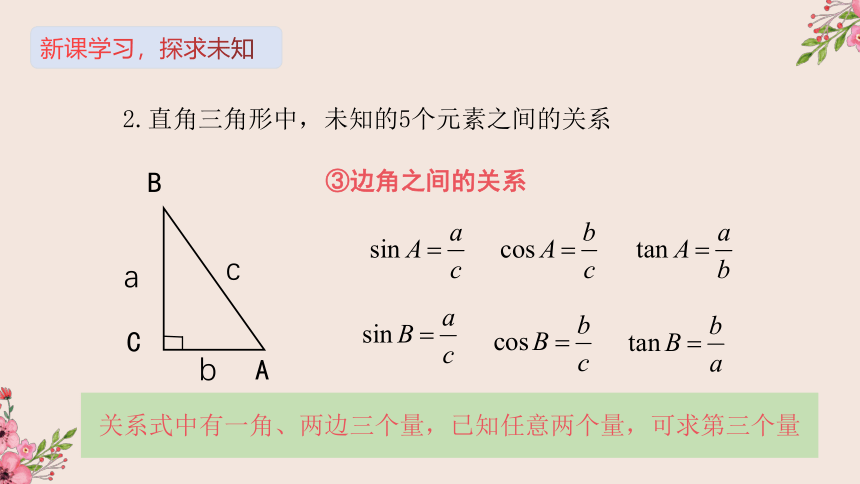
③边角之间的关系
B
C
A
c
b
a
关系式中有一角、两边三个量,已知任意两个量,可求第三个量
新课学习,探求未知
B
C
A
c
b
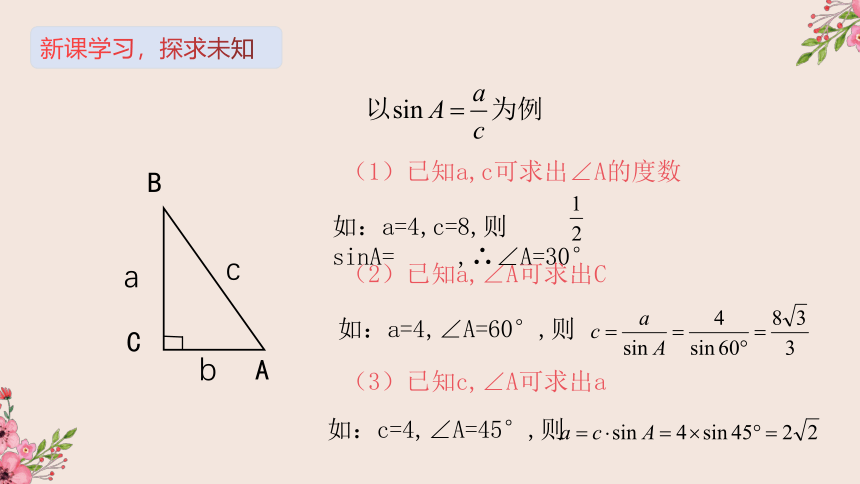
a
(1)已知a,c可求出∠A的度数
如:a=4,c=8,则sinA=
,∴∠A=30°
(2)已知a,∠A可求出C
如:a=4,∠A=60°,则
(3)已知c,∠A可求出a
如:c=4,∠A=45°,则
新课学习,探求未知
2.直角三角形中,未知的5个元素之间的关系
②两个锐角之间的关系
B
C
A
c
b
a
根据以上关系,若知道五个元素中的两个元素(至少有一个是边),就可以求出其他三个元素.
①三边之间的关系
③边角之间的关系:
巩固新知,提升能力
例1.(课本115页例1)如图,在Rt△ABC中,∠C=90°,∠A=34°,AC=6.解这个直角三角形.(结果精确到0.01)(sin34°≈0.60,cos34°≈0.56,tan34°≈0.67)
A
C
B
34°
6
尝试独立解决,再一起交流
(1)欲求的未知元素有哪些?
∠B、BC、AB
(2)如何求∠B?
利用∠A+∠B=90°
二、解直角三角形的方法与步骤
巩固新知,提升能力
A
C
B
34°
6
(3)如何求BC?
所求的BC与已知的AC的比构成tanA,用tanA=BC:AC来求.
(4)如何求AB?
所求的AB与已知的AC的比构成cosA,用cosA=AC:AB来求.
把所求的线段和已知的线段放到一个比例式中,确定是哪个角的哪个三角函数
巩固新知,提升能力
sin34°≈0.60,
cos34°≈0.83,
tan34°≈0.67
A
C
B
34°
6
解:∠B=90°-∠A=90°-34°=56°.
在Rt△ABC中
∴BC=AC·tanA=6×tan34°≈6×0.67=4.02
想一想:求AB时,用勾股定理好不好?
指明是哪个直角三角形
指明是哪个三角函数
导公式、计算
不好,会增大结果的误差,应尽可能用原题中的数据.
巩固新知,提升能力
例2.(课本115页例2)如图,在Rt△ABC中,∠C=90°,AC=15,BC=8.解这个直角三角形.(角度精确到度)
A
C
B
8
15
(1)欲求的未知元素有哪些?
∠A、∠B、AB
(2)如何求∠A?
已知的BC和AC的比构成tanA,用tanA=BC:AC来求.
sin28°≈0.47,
cos28°≈0.88,
tan28°≈0.53
巩固新知,提升能力
例2.(课本115页例2)如图,在Rt△ABC中,∠C=90°,AC=15,BC=8.解这个直角三角形.(角度精确到度)
A
C
B
8
15
(3)如何求∠B?
(4)如何求AB?
利用勾股定理.
利用∠A+∠B=90°.
巩固新知,提升能力
A
C
B
8
解:在Rt△ABC中
∴∠A=28°
想一想:求AB时,用sinA好不好?
由边长可导出角度,是不是很神奇?
不好,会增大结果的误差,应尽可能用原题中的数据.
sin28°≈0.47,
cos28°≈0.88,
tan28°≈0.53
15
∴∠B=90°-∠A=90°-28°=62°.
反思总结,夯实积累
想一想:(1)解直角三角形的作用
①求角的度数
②求边长
想一想:(2)求角度的方法
①直角三角形的两锐角互余
②三角函数值
想一想:(3)求边长的方法
①三角函数
②勾股定理
综合运用,锻炼思维
4
150°
例1:如图,在△ABC中,∠ABC=150°,AC=4,tanB=
.求BC的长.
分析:三角函数放到直角三角形中才能用,如何做辅助线,能让∠B到一个直角三角形中?
三、解直角三角形的综合运用
A
C
B
①过点C向AB做垂线
×
破坏了150°
②过点A向BC做垂线
√
D
没有破坏150°,同时将已知边AC放到了直角三角形中.
综合运用,锻炼思维
4
150°
例1:如图,在△ABC中,∠ABC=150°,AC=4,tanB=
.求BC的长.
A
C
B
D
在Rt△ABD中
解:过点A作AD⊥BC的延长线于点D
在Rt△ACD中,∠ACD=180°-150°=30°
∴AD=
AB=2
∴BC=BD-CD=16-2√3
综合运用,锻炼思维
做辅助线是要考虑:
①让直角三角形出现;
②不能破坏∠A;
③
使已知边AB、DC落在直角三角形中.
想一想:如何让图中出现直角三角形?
例2:在四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,sinA=
.求AD的长.
6
4
A
C
B
D
添加辅助线
综合运用,锻炼思维
解:延长AD、BC相交与点E
6
4
A
C
B
D
由勾股定理可得,AB=3k=6
∴k=2
∴AE=5k=10,BE=4k=8
E
∵∠A+∠E=90°,∠DCE+∠E=90°
∴∠DCE=∠A
反思总结,夯实积累
(1)做垂直,出现直角三角形.
运用三角函数需要出现直角三角形,常见的辅助线有
A
C
B
D
A
C
B
D
E
(2)做延长,出现直角三角形.
课堂小测
1.
在Rt△ABC中,∠C=90°,AC=1,AB=2,则下列结论中正确的是(
)
A、
∠B=30°
B、BC=1
C、
∠A=30°
C、∠A=45°
A
课堂小测
2.
如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直(A,C,B在同一条直线上),设∠CAB=α,那么拉线BC的长度为________.
D
C
B
A
课堂小测
3.
如图,在△ABC中,BC=2,△ABC的面积=3,∠ABC=135°。则AC的长度为________.
C
B
A
D
一、解直角三角形的定义.
回顾与小结
二、直角三角形中的三边关系、两锐角关系、边角关系.
三、解直角三角形的书写格式及注意事项.
四、常用的作辅助线的方法.
同学们再见
26.3
解直角三角形
冀教版九上
第二十六
解直角三角形
新课引入
新课学习
典例精析
测试小结
学
习
目
标
冀教版九上
1.梳理、归纳直角三角形章三边、两锐角、边角之间的关系.
2.选择恰当的直角三角形中三边、两锐角、边角之间的关系,解直角三角形.
3.体会解直角三角形的过程,规范解题格式.
创设情境,引入新课
解下列方程或方程组:
x=2
(1)2x=4
{
(2)
x-y=4
x+y=0
(3)
a=3
a+b=0
a+b+c=-1
{
x=2.y=-2
a=3,b=-3,c=-1.
怎样理解解方程中的“解”?
就是将方程中所有未知的数求出.
创设情境,引入新课
观察:在直角三角形中,共有3个角、3条边6个元素,其中直角是确定的,其他5个元素是不确定的.
想一想:类比解方程,推测什么是解直角三角形?
C
A
B
新课学习,探求未知
B
C
A
一、解直角三角形
在直角三角形中,除直角外,还有三条边和两个锐角共五个元素.由这五个元素中的已知元素求出其余未知元素的过程,叫做解直角三角形.
新课学习,探求未知
2.直角三角形中,未知的5个元素之间的关系
①三边之间的关系
B
C
A
c
b
a
已知任意两边可求出第三边
新课学习,探求未知
2.直角三角形中,未知的5个元素之间的关系
②两个锐角之间的关系
B
C
A
c
b
a
已知一个锐角可求出另一个锐角
新课学习,探求未知
2.直角三角形中,未知的5个元素之间的关系
③边角之间的关系
B
C
A
c
b
a
关系式中有一角、两边三个量,已知任意两个量,可求第三个量
新课学习,探求未知
B
C
A
c
b
a
(1)已知a,c可求出∠A的度数
如:a=4,c=8,则sinA=
,∴∠A=30°
(2)已知a,∠A可求出C
如:a=4,∠A=60°,则
(3)已知c,∠A可求出a
如:c=4,∠A=45°,则
新课学习,探求未知
2.直角三角形中,未知的5个元素之间的关系
②两个锐角之间的关系
B
C
A
c
b
a
根据以上关系,若知道五个元素中的两个元素(至少有一个是边),就可以求出其他三个元素.
①三边之间的关系
③边角之间的关系:
巩固新知,提升能力
例1.(课本115页例1)如图,在Rt△ABC中,∠C=90°,∠A=34°,AC=6.解这个直角三角形.(结果精确到0.01)(sin34°≈0.60,cos34°≈0.56,tan34°≈0.67)
A
C
B
34°
6
尝试独立解决,再一起交流
(1)欲求的未知元素有哪些?
∠B、BC、AB
(2)如何求∠B?
利用∠A+∠B=90°
二、解直角三角形的方法与步骤
巩固新知,提升能力
A
C
B
34°
6
(3)如何求BC?
所求的BC与已知的AC的比构成tanA,用tanA=BC:AC来求.
(4)如何求AB?
所求的AB与已知的AC的比构成cosA,用cosA=AC:AB来求.
把所求的线段和已知的线段放到一个比例式中,确定是哪个角的哪个三角函数
巩固新知,提升能力
sin34°≈0.60,
cos34°≈0.83,
tan34°≈0.67
A
C
B
34°
6
解:∠B=90°-∠A=90°-34°=56°.
在Rt△ABC中
∴BC=AC·tanA=6×tan34°≈6×0.67=4.02
想一想:求AB时,用勾股定理好不好?
指明是哪个直角三角形
指明是哪个三角函数
导公式、计算
不好,会增大结果的误差,应尽可能用原题中的数据.
巩固新知,提升能力
例2.(课本115页例2)如图,在Rt△ABC中,∠C=90°,AC=15,BC=8.解这个直角三角形.(角度精确到度)
A
C
B
8
15
(1)欲求的未知元素有哪些?
∠A、∠B、AB
(2)如何求∠A?
已知的BC和AC的比构成tanA,用tanA=BC:AC来求.
sin28°≈0.47,
cos28°≈0.88,
tan28°≈0.53
巩固新知,提升能力
例2.(课本115页例2)如图,在Rt△ABC中,∠C=90°,AC=15,BC=8.解这个直角三角形.(角度精确到度)
A
C
B
8
15
(3)如何求∠B?
(4)如何求AB?
利用勾股定理.
利用∠A+∠B=90°.
巩固新知,提升能力
A
C
B
8
解:在Rt△ABC中
∴∠A=28°
想一想:求AB时,用sinA好不好?
由边长可导出角度,是不是很神奇?
不好,会增大结果的误差,应尽可能用原题中的数据.
sin28°≈0.47,
cos28°≈0.88,
tan28°≈0.53
15
∴∠B=90°-∠A=90°-28°=62°.
反思总结,夯实积累
想一想:(1)解直角三角形的作用
①求角的度数
②求边长
想一想:(2)求角度的方法
①直角三角形的两锐角互余
②三角函数值
想一想:(3)求边长的方法
①三角函数
②勾股定理
综合运用,锻炼思维
4
150°
例1:如图,在△ABC中,∠ABC=150°,AC=4,tanB=
.求BC的长.
分析:三角函数放到直角三角形中才能用,如何做辅助线,能让∠B到一个直角三角形中?
三、解直角三角形的综合运用
A
C
B
①过点C向AB做垂线
×
破坏了150°
②过点A向BC做垂线
√
D
没有破坏150°,同时将已知边AC放到了直角三角形中.
综合运用,锻炼思维
4
150°
例1:如图,在△ABC中,∠ABC=150°,AC=4,tanB=
.求BC的长.
A
C
B
D
在Rt△ABD中
解:过点A作AD⊥BC的延长线于点D
在Rt△ACD中,∠ACD=180°-150°=30°
∴AD=
AB=2
∴BC=BD-CD=16-2√3
综合运用,锻炼思维
做辅助线是要考虑:
①让直角三角形出现;
②不能破坏∠A;
③
使已知边AB、DC落在直角三角形中.
想一想:如何让图中出现直角三角形?
例2:在四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,sinA=
.求AD的长.
6
4
A
C
B
D
添加辅助线
综合运用,锻炼思维
解:延长AD、BC相交与点E
6
4
A
C
B
D
由勾股定理可得,AB=3k=6
∴k=2
∴AE=5k=10,BE=4k=8
E
∵∠A+∠E=90°,∠DCE+∠E=90°
∴∠DCE=∠A
反思总结,夯实积累
(1)做垂直,出现直角三角形.
运用三角函数需要出现直角三角形,常见的辅助线有
A
C
B
D
A
C
B
D
E
(2)做延长,出现直角三角形.
课堂小测
1.
在Rt△ABC中,∠C=90°,AC=1,AB=2,则下列结论中正确的是(
)
A、
∠B=30°
B、BC=1
C、
∠A=30°
C、∠A=45°
A
课堂小测
2.
如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直(A,C,B在同一条直线上),设∠CAB=α,那么拉线BC的长度为________.
D
C
B
A
课堂小测
3.
如图,在△ABC中,BC=2,△ABC的面积=3,∠ABC=135°。则AC的长度为________.
C
B
A
D
一、解直角三角形的定义.
回顾与小结
二、直角三角形中的三边关系、两锐角关系、边角关系.
三、解直角三角形的书写格式及注意事项.
四、常用的作辅助线的方法.
同学们再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
