2020-2021学年沪科版八年级上册数学第14章全等三角形培优试卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年沪科版八年级上册数学第14章全等三角形培优试卷(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 120.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-03 00:00:00 | ||
图片预览



文档简介
沪科版2020-2021八年级第一学期数学培优试卷(含答案)
第
14
章
全等三角形(全章)
一、选择题:
1、下列命题中真命题的个数有(
)
(1)形状相同的两个三角形是全等形;(2)在两个三角形中,相等的角是对应角,相等的边是对应边;
(3)全等三角形对应边上的高、中线及对应角平分线分别相等。
A.
3个
B.
2个
C.
1个
D.
0个
2、在△ABC和△A?B?C?中,AB
=
A?B?,∠A
=
∠A?,若证△ABC≌△A?B?C?,还要从下面选择一个,错误的做法是(
)
A.
∠B
=
∠B?
B.
∠C
=
∠C?
C.
BC
=
B?C?
D.
AC
=
A?C?
3、如图,已知
AD=CB,补充条件,使△ABD≌△CDB,不正确的是(
)
A.
AB=CD
B.
∠ADB
=
∠CBD
C.
AD∥BC
D.
∠A
=
∠C
第
3
题
第
5
题
第
6
题
4、下列可使两个直角三角形全等的条件是(
)
A.
一条边对应相等
B.
两条直角边对应相等
C.
一个锐角对应相等
D.
两个锐角对应相等
5、如图,AD是△ABC的中线,E、F分别是AD和AD延长线上的点,且DE
=
DF,连接BF、CE,下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有(
)
A.
1个
B.
2个
C.
3个
D.
4个
6、如图,BE=CD,AD=AE,∠1
=∠2=110°,∠BAE
=60°,则
∠CAE等于(
)
A.
20°
B.
30°
C.
40°
D.
50°
7、如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点Cˊ的位置,则图中的一个等腰直角三角形是(
)
A.
△ADC
B.
△BDCˊ
C.
△ADCˊ
D.
不存在
第
7
题
第
8
题
8、如图,P是∠BAC的平分线AD上的一点,PE⊥AB于E,PF⊥AC于F,下列结论不正确的是(
)
A
PE=PF
B.
AE=AF
C.
△APE≌△APF
D.
AP=PE+PF
9、如图,点E在△ABC外部,点D在△ABC的BC边上,DE交AC于F,若∠1
=∠2=∠3,AE=AC,则(
)
A.
△ABD≌△AFE
B.
△AFE≌△ADC
C.
△AFE≌△DFC
D.
△ABC≌△ADE
第
9
题
第
10
题
10、如图所示,在Rt△ABC中,AD是斜边上的高,∠ABC的平分线分别交AD、AC于点F、E,EG⊥BC于G,下列结论正确的是(
)
A.
∠C=∠ABC
B.
BA=BG
C.
AE=CE
D.
AF=FD
二、填空题:
11、在△ABC中,AC>BC>AB,且△ABC≌△DEF,则在△DEF中,
<
<
(填边)。
12、如图,Rt△ABC≌Rt△EFC,并且CF=5cm,∠EFC=52°,则BC=
,∠A=
。
第
12
题
第
13
题
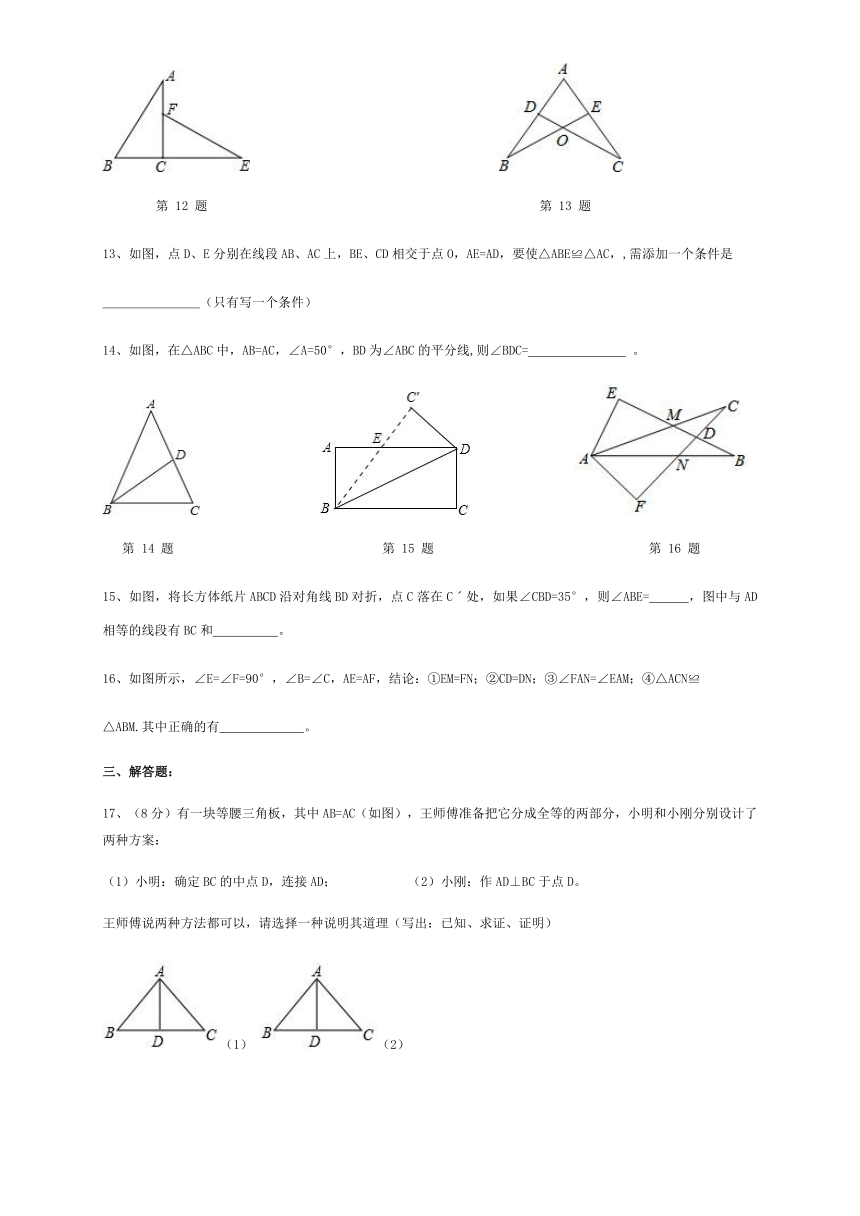
13、如图,点D、E分别在线段AB、AC上,BE、CD相交于点O,AE=AD,要使△ABE≌△AC,,需添加一个条件是
(只有写一个条件)
14、如图,在△ABC中,AB=AC,∠A=50°,BD为∠ABC的平分线,则∠BDC=
。
第
14
题
第
15
题
第
16
题
15、如图,将长方体纸片ABCD沿对角线BD对折,点C落在Cˊ处,如果∠CBD=35°,则∠ABE=
,图中与AD相等的线段有BC和
。
16、如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌
△ABM.其中正确的有
。
三、解答题:
17、(8分)有一块等腰三角板,其中AB=AC(如图),王师傅准备把它分成全等的两部分,小明和小刚分别设计了两种方案:
(1)小明:确定BC的中点D,连接AD;
(2)小刚:作AD⊥BC于点D。
王师傅说两种方法都可以,请选择一种说明其道理(写出:已知、求证、证明)
(1)
(2)
18、(8分)如图,AB=AE,∠1=∠2,∠C=∠D,求证:△ABC≌△AED
19、(9分)如图,在△ABC中,AD为BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28cm2,AB=20cm,AC=8cm,求DE的长。
20、(9分)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE。
(1)求证:CE=CF;
(2)若G在AD上,且∠GCE=45°,则:GE=BE+GD成立吗?为什么?
21、(12分)如图,在四边形ABCD中,AD//BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
附加题(10分)
如图所示,已知∠1=∠2,EF⊥AD于P,交BC延长线于M,求证:2∠M=∠ACB-∠B
沪科版2020-2021八年级第一学期数学培优试卷答案
一、选择题:
1
2
3
4
5
6
7
8
9
10
C
C
D
B
D
A
B
D
D
B
二、填空题:11、DE、EF、DF;
12、5cm,38°;13、AB=AC;14、82.5°;15、20°,BC?;
16、①③④
三、解答题:17、(选择1)已知AB=AC,D是BC的中点。求证:△ABD≌△ACD
证明:∵D是BC的中点,∴BD=CD,在△ABD和△ACD中,AB=AC,BD=CD,AD=AD,∴△ABD≌△ACD(SSS)
(选择2)已知AB=AC,AD⊥BC。求证:△ABD≌△ACD
证明:∵AD⊥BC,∴∠ADB=∠ADC=90°,在Rt△ABD和Rr△ACD中,AB=AC,AD=AD,∴△ABD≌△ACD(HL)
18、证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD,
∵在△ABC和△AED中,∠D=∠C,∠BAC=∠EAD,AB=AE,∴△ABC≌△AED(AAS).
19、解:∵AD为BAC的平分线,∴∠BAD=∠CAD,∵DE⊥AB,E,DF⊥AC,∴∠AED=∠AFD=90°
在△AED和△AFD中,∠BAD=∠CAD,AD=AD,∠AED=∠AFD=90°,∴△AED≌△AFD,
∴DE=DF,
在△ABC中,∵△ABC面积是28cm2,AB=20cm,AC=8cm,∴S△ABC=AB?DE+AC?DF=28,即×20×DE+×8×DF=28,解得DE=2cm.
20、(1)证明:∵
在正方形ABCD中,E是AB上一点,F是AD延长线上一点,∴BC=CD且∠B=∠CDF=90°,
在△CBE和△CDF中,BC=CD,∠B=∠CDF=90°,DF=BE,∴△CBE≌△CDF(SAS).∴CE=CF.
(2)解:GE=BE+GD成立.理由是:∵由(1)得:△CBE≌△CDF,∴CE=CF且∠BCE=∠DCF,∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∵∠GCE=45°,∴∠GCF=∠GCE=45°.在△ECG和△FCG中,CE=CF,∠GCE=∠GCF=45°,GC=GC,∴△ECG≌△FCG(SAS).∴GE=GF.∴GE=DF+GD=BE+GD.
21、(1)证明:∵AD∥BC,∴∠ADE=∠BFE,∵E为AB的中点,∴AE=BE,在△ADE和△BFE中,∠ADE=∠BFE,
∠AED=∠BEF,AE=BE,∴△ADE≌△BFE(AAS);
(2)解:EG⊥DF,理由为:连接EG,∵∠GDF=∠ADE,∠ADE=∠BFE,∴∠GDF=∠GFE,∴△GDF是等腰三角形,∴GF=GD由(1)△ADE≌△BFE得:DE=FE,在△GEF和△DED中,GE=GF,DE=FE,GE=GE,∴△GEF≌△DED,
∴∠GEF=∠GED=×180°=90°,∴EG⊥DF.
附加题:证明:∵EF⊥AD,∴∠APE=∠APF=90°,在△AEP和△AFP中,∠1=∠2,AP=AP,∠APE=∠APF=90°,
∴△AEP≌△AFP(ASA),∠AEP=∠AFP(全等三角形对应角相等),
又∵∠AEP=∠B+∠M(三角形外角性质),
即:∠B=∠AEP-∠M;又∵∠ACB=∠MFC+∠M(三角形外角性质),即∠ACB=∠AFP+∠M,∴∠ACB-∠B=(∠AFP+∠M)-(∠AEP-∠M)=2∠M;即:2∠M=∠ACB-∠B
第
14
章
全等三角形(全章)
一、选择题:
1、下列命题中真命题的个数有(
)
(1)形状相同的两个三角形是全等形;(2)在两个三角形中,相等的角是对应角,相等的边是对应边;
(3)全等三角形对应边上的高、中线及对应角平分线分别相等。
A.
3个
B.
2个
C.
1个
D.
0个
2、在△ABC和△A?B?C?中,AB
=
A?B?,∠A
=
∠A?,若证△ABC≌△A?B?C?,还要从下面选择一个,错误的做法是(
)
A.
∠B
=
∠B?
B.
∠C
=
∠C?
C.
BC
=
B?C?
D.
AC
=
A?C?
3、如图,已知
AD=CB,补充条件,使△ABD≌△CDB,不正确的是(
)
A.
AB=CD
B.
∠ADB
=
∠CBD
C.
AD∥BC
D.
∠A
=
∠C
第
3
题
第
5
题
第
6
题
4、下列可使两个直角三角形全等的条件是(
)
A.
一条边对应相等
B.
两条直角边对应相等
C.
一个锐角对应相等
D.
两个锐角对应相等
5、如图,AD是△ABC的中线,E、F分别是AD和AD延长线上的点,且DE
=
DF,连接BF、CE,下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有(
)
A.
1个
B.
2个
C.
3个
D.
4个
6、如图,BE=CD,AD=AE,∠1
=∠2=110°,∠BAE
=60°,则
∠CAE等于(
)
A.
20°
B.
30°
C.
40°
D.
50°
7、如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点Cˊ的位置,则图中的一个等腰直角三角形是(
)
A.
△ADC
B.
△BDCˊ
C.
△ADCˊ
D.
不存在
第
7
题
第
8
题
8、如图,P是∠BAC的平分线AD上的一点,PE⊥AB于E,PF⊥AC于F,下列结论不正确的是(
)
A
PE=PF
B.
AE=AF
C.
△APE≌△APF
D.
AP=PE+PF
9、如图,点E在△ABC外部,点D在△ABC的BC边上,DE交AC于F,若∠1
=∠2=∠3,AE=AC,则(
)
A.
△ABD≌△AFE
B.
△AFE≌△ADC
C.
△AFE≌△DFC
D.
△ABC≌△ADE
第
9
题
第
10
题
10、如图所示,在Rt△ABC中,AD是斜边上的高,∠ABC的平分线分别交AD、AC于点F、E,EG⊥BC于G,下列结论正确的是(
)
A.
∠C=∠ABC
B.
BA=BG
C.
AE=CE
D.
AF=FD
二、填空题:
11、在△ABC中,AC>BC>AB,且△ABC≌△DEF,则在△DEF中,
<
<
(填边)。
12、如图,Rt△ABC≌Rt△EFC,并且CF=5cm,∠EFC=52°,则BC=
,∠A=
。
第
12
题
第
13
题
13、如图,点D、E分别在线段AB、AC上,BE、CD相交于点O,AE=AD,要使△ABE≌△AC,,需添加一个条件是
(只有写一个条件)
14、如图,在△ABC中,AB=AC,∠A=50°,BD为∠ABC的平分线,则∠BDC=
。
第
14
题
第
15
题
第
16
题
15、如图,将长方体纸片ABCD沿对角线BD对折,点C落在Cˊ处,如果∠CBD=35°,则∠ABE=
,图中与AD相等的线段有BC和
。
16、如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌
△ABM.其中正确的有
。
三、解答题:
17、(8分)有一块等腰三角板,其中AB=AC(如图),王师傅准备把它分成全等的两部分,小明和小刚分别设计了两种方案:
(1)小明:确定BC的中点D,连接AD;
(2)小刚:作AD⊥BC于点D。
王师傅说两种方法都可以,请选择一种说明其道理(写出:已知、求证、证明)
(1)
(2)
18、(8分)如图,AB=AE,∠1=∠2,∠C=∠D,求证:△ABC≌△AED
19、(9分)如图,在△ABC中,AD为BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28cm2,AB=20cm,AC=8cm,求DE的长。
20、(9分)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE。
(1)求证:CE=CF;
(2)若G在AD上,且∠GCE=45°,则:GE=BE+GD成立吗?为什么?
21、(12分)如图,在四边形ABCD中,AD//BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
附加题(10分)
如图所示,已知∠1=∠2,EF⊥AD于P,交BC延长线于M,求证:2∠M=∠ACB-∠B
沪科版2020-2021八年级第一学期数学培优试卷答案
一、选择题:
1
2
3
4
5
6
7
8
9
10
C
C
D
B
D
A
B
D
D
B
二、填空题:11、DE、EF、DF;
12、5cm,38°;13、AB=AC;14、82.5°;15、20°,BC?;
16、①③④
三、解答题:17、(选择1)已知AB=AC,D是BC的中点。求证:△ABD≌△ACD
证明:∵D是BC的中点,∴BD=CD,在△ABD和△ACD中,AB=AC,BD=CD,AD=AD,∴△ABD≌△ACD(SSS)
(选择2)已知AB=AC,AD⊥BC。求证:△ABD≌△ACD
证明:∵AD⊥BC,∴∠ADB=∠ADC=90°,在Rt△ABD和Rr△ACD中,AB=AC,AD=AD,∴△ABD≌△ACD(HL)
18、证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD,
∵在△ABC和△AED中,∠D=∠C,∠BAC=∠EAD,AB=AE,∴△ABC≌△AED(AAS).
19、解:∵AD为BAC的平分线,∴∠BAD=∠CAD,∵DE⊥AB,E,DF⊥AC,∴∠AED=∠AFD=90°
在△AED和△AFD中,∠BAD=∠CAD,AD=AD,∠AED=∠AFD=90°,∴△AED≌△AFD,
∴DE=DF,
在△ABC中,∵△ABC面积是28cm2,AB=20cm,AC=8cm,∴S△ABC=AB?DE+AC?DF=28,即×20×DE+×8×DF=28,解得DE=2cm.
20、(1)证明:∵
在正方形ABCD中,E是AB上一点,F是AD延长线上一点,∴BC=CD且∠B=∠CDF=90°,
在△CBE和△CDF中,BC=CD,∠B=∠CDF=90°,DF=BE,∴△CBE≌△CDF(SAS).∴CE=CF.
(2)解:GE=BE+GD成立.理由是:∵由(1)得:△CBE≌△CDF,∴CE=CF且∠BCE=∠DCF,∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∵∠GCE=45°,∴∠GCF=∠GCE=45°.在△ECG和△FCG中,CE=CF,∠GCE=∠GCF=45°,GC=GC,∴△ECG≌△FCG(SAS).∴GE=GF.∴GE=DF+GD=BE+GD.
21、(1)证明:∵AD∥BC,∴∠ADE=∠BFE,∵E为AB的中点,∴AE=BE,在△ADE和△BFE中,∠ADE=∠BFE,
∠AED=∠BEF,AE=BE,∴△ADE≌△BFE(AAS);
(2)解:EG⊥DF,理由为:连接EG,∵∠GDF=∠ADE,∠ADE=∠BFE,∴∠GDF=∠GFE,∴△GDF是等腰三角形,∴GF=GD由(1)△ADE≌△BFE得:DE=FE,在△GEF和△DED中,GE=GF,DE=FE,GE=GE,∴△GEF≌△DED,
∴∠GEF=∠GED=×180°=90°,∴EG⊥DF.
附加题:证明:∵EF⊥AD,∴∠APE=∠APF=90°,在△AEP和△AFP中,∠1=∠2,AP=AP,∠APE=∠APF=90°,
∴△AEP≌△AFP(ASA),∠AEP=∠AFP(全等三角形对应角相等),
又∵∠AEP=∠B+∠M(三角形外角性质),
即:∠B=∠AEP-∠M;又∵∠ACB=∠MFC+∠M(三角形外角性质),即∠ACB=∠AFP+∠M,∴∠ACB-∠B=(∠AFP+∠M)-(∠AEP-∠M)=2∠M;即:2∠M=∠ACB-∠B
