3.1.2 等式的性质
图片预览







文档简介
(共21张PPT)
祁迎春
回顾: 什么是方程?
什么是方程的解?
含有未知数的等式——方程
使方程中等号左右两边相等的未知数的值——方程的解
估计下列方程的解:
学习目标:
1.掌握等式的两条性质。
2.会利用等式的性质解方程并检
验方程。
m+n = n+m
x+2x = 3x
3×3+1 = 5×2
3x+1 = 5y
观察
这4个式子的共同点是什么?
用等号“=”来表示相等关系的式子,叫做等式。a=b
有“=”
是等式
上述这组式子中,( )是等式, ( ) 不是等式,为什么?
①4+x=7, ② 2x, ③ 3x+1,
④ a+b=b+a, ⑤ a2+b2 ⑥ c=2πr
⑦ 1+2=3, ⑧ ab, ⑨ S= ah,
⑩ 2x-3y>0
2
3
1
2
①④⑥⑦⑨
②③⑤⑧⑩
判 断
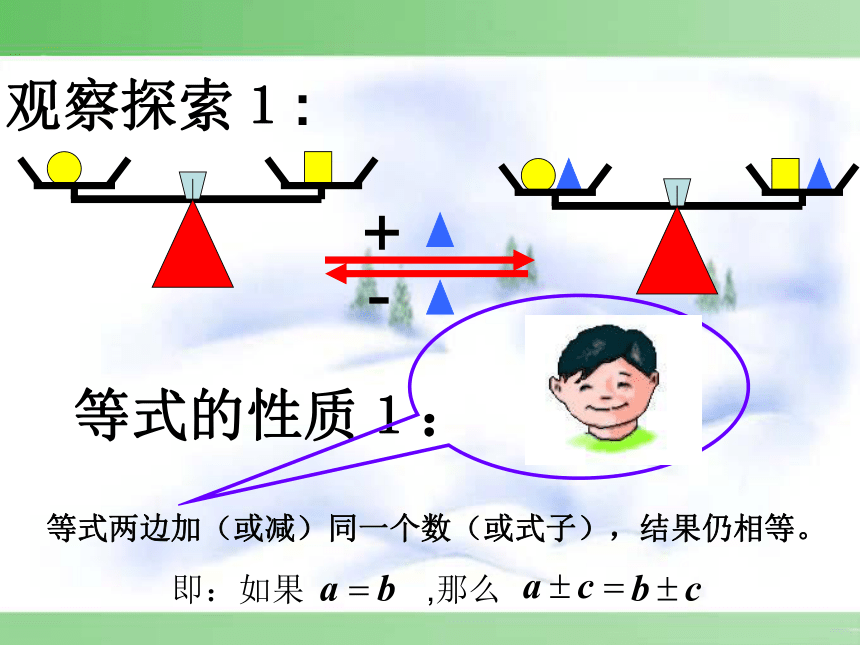
观察探索1:
+
-
等式两边加(或减)同一个数(或式子),结果仍相等。
等式的性质1:
即:如果 ,那么
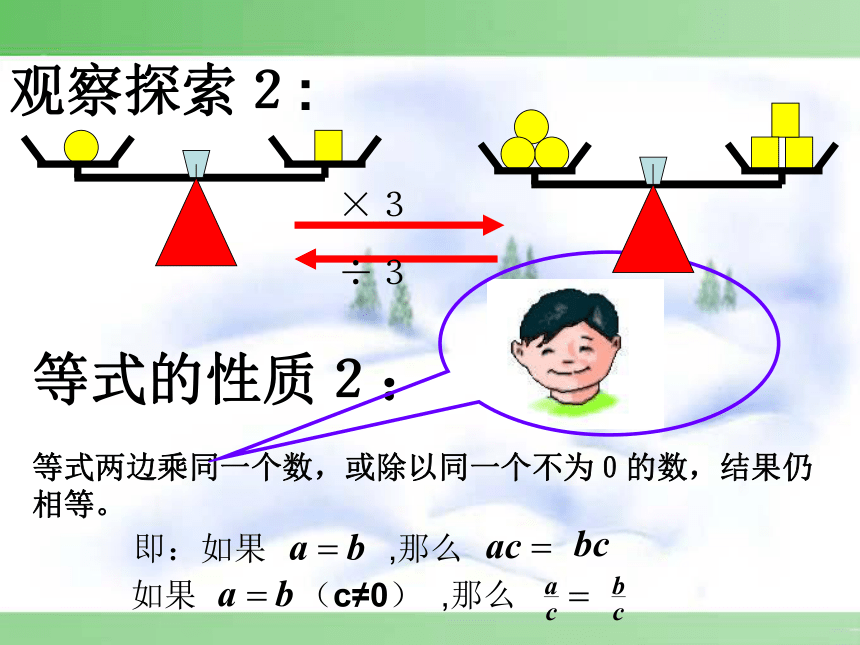
观察探索2:
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
等式的性质2:
即:如果 ,那么
如果 (c≠0) ,那么
×3
÷3
等式的性质1:
等式两边加(或减)
同一个数(或式子子),结果仍相等。
等式的性质2:
等式两边乘同一
个数,或除以同一
个不为0数,结果仍
相等。
等式的两个性质
用等式的性质变形时,
①两边必须同时进行计算;
②加(或减),乘(或除以)的数必须是同一个数;
③除数不能为0.
(1)如果x=y,那么 ( )
(2)如果x=y,那么 ( )
(3)如果x=y,那么 ( )
(4)如果x=y,那么 ( )
(5)如果x=y,那么 ( )
判断对错,对的说明根据等式的哪一条性质;错的说出为什么。
×
√
×
×
√
应用
例1:用适当的数或整式填空,使所得结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形(改变式子的形状)的。
①、如果2x = 5 - 3x,那么2x +( )= 5
②、如果0.2x = 10, 那么x =( )
解:①、2x +( 3x )= 5
根据等式性质 1,等式两边都加上 3x。
②、x = ( 50 )
根据等式性质 2,等式两边都除以 0.2 或乘以 5。
+2 +2
=
练习1:填空
① 若 x-2 = 3,根据__________,得到 x-2 = 3 ,即 x = 5 。
② 若 -4 x = 3,根据___________,
得到 ,即x =____ 。
等式的性质1
等式的性质2
所以解一元一次 方程就是利用等式的性质
质把方程转化为x=a(常数)的形式
利用等式的性质解下列方程:
解:
(1)两边减7,得
(3)两边加5,得
(2)两边同除以-5,得
于是
于是
化简,得
两边同乘-3,得
如何检验?
将 代入方程 的左边,得
方程的左右两边相等,所以 是方程的解。
注意:要带入原方程。
下面的解法对不对?如果不对,错在哪里?应怎样改正?
(1)解方程:x+12=34
解:x+12=34=x+12 -12=34 -12=x=22
(2)解方程:-9x+3=6
解:-9x+3-3=6-3
=
x=-3
解: x+12=34
x+12 -12=34 -12
x=22
练习2:下列各式的变形正确的是( )
A.由 ,得到 x = 2
B.由 ,得到 x = 1
C.由-2 a = -3,得到 a =
D.由 x-1 = 4,得到 x = 5
D
x = 0
x = 9
a =
练习3:利用等式性质解下列方程并检验:
(1)x-5 = 6 (2) 0.3x = 45
(3)2 - x = 3 (4)5x+4=0
1
4
小结:
1、等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
2、等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
如果 a = b,那么 a ± c = b ± c
如果 a = b,那么 a c = b c
如果 a = b,那么 (c≠ 0)
3、解一元一次方程的实质就是利用等式的
性质求出未知数的值x=a(常数)
下课了!
祁迎春
回顾: 什么是方程?
什么是方程的解?
含有未知数的等式——方程
使方程中等号左右两边相等的未知数的值——方程的解
估计下列方程的解:
学习目标:
1.掌握等式的两条性质。
2.会利用等式的性质解方程并检
验方程。
m+n = n+m
x+2x = 3x
3×3+1 = 5×2
3x+1 = 5y
观察
这4个式子的共同点是什么?
用等号“=”来表示相等关系的式子,叫做等式。a=b
有“=”
是等式
上述这组式子中,( )是等式, ( ) 不是等式,为什么?
①4+x=7, ② 2x, ③ 3x+1,
④ a+b=b+a, ⑤ a2+b2 ⑥ c=2πr
⑦ 1+2=3, ⑧ ab, ⑨ S= ah,
⑩ 2x-3y>0
2
3
1
2
①④⑥⑦⑨
②③⑤⑧⑩
判 断
观察探索1:
+
-
等式两边加(或减)同一个数(或式子),结果仍相等。
等式的性质1:
即:如果 ,那么
观察探索2:
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
等式的性质2:
即:如果 ,那么
如果 (c≠0) ,那么
×3
÷3
等式的性质1:
等式两边加(或减)
同一个数(或式子子),结果仍相等。
等式的性质2:
等式两边乘同一
个数,或除以同一
个不为0数,结果仍
相等。
等式的两个性质
用等式的性质变形时,
①两边必须同时进行计算;
②加(或减),乘(或除以)的数必须是同一个数;
③除数不能为0.
(1)如果x=y,那么 ( )
(2)如果x=y,那么 ( )
(3)如果x=y,那么 ( )
(4)如果x=y,那么 ( )
(5)如果x=y,那么 ( )
判断对错,对的说明根据等式的哪一条性质;错的说出为什么。
×
√
×
×
√
应用
例1:用适当的数或整式填空,使所得结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形(改变式子的形状)的。
①、如果2x = 5 - 3x,那么2x +( )= 5
②、如果0.2x = 10, 那么x =( )
解:①、2x +( 3x )= 5
根据等式性质 1,等式两边都加上 3x。
②、x = ( 50 )
根据等式性质 2,等式两边都除以 0.2 或乘以 5。
+2 +2
=
练习1:填空
① 若 x-2 = 3,根据__________,得到 x-2 = 3 ,即 x = 5 。
② 若 -4 x = 3,根据___________,
得到 ,即x =____ 。
等式的性质1
等式的性质2
所以解一元一次 方程就是利用等式的性质
质把方程转化为x=a(常数)的形式
利用等式的性质解下列方程:
解:
(1)两边减7,得
(3)两边加5,得
(2)两边同除以-5,得
于是
于是
化简,得
两边同乘-3,得
如何检验?
将 代入方程 的左边,得
方程的左右两边相等,所以 是方程的解。
注意:要带入原方程。
下面的解法对不对?如果不对,错在哪里?应怎样改正?
(1)解方程:x+12=34
解:x+12=34=x+12 -12=34 -12=x=22
(2)解方程:-9x+3=6
解:-9x+3-3=6-3
=
x=-3
解: x+12=34
x+12 -12=34 -12
x=22
练习2:下列各式的变形正确的是( )
A.由 ,得到 x = 2
B.由 ,得到 x = 1
C.由-2 a = -3,得到 a =
D.由 x-1 = 4,得到 x = 5
D
x = 0
x = 9
a =
练习3:利用等式性质解下列方程并检验:
(1)x-5 = 6 (2) 0.3x = 45
(3)2 - x = 3 (4)5x+4=0
1
4
小结:
1、等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
2、等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
如果 a = b,那么 a ± c = b ± c
如果 a = b,那么 a c = b c
如果 a = b,那么 (c≠ 0)
3、解一元一次方程的实质就是利用等式的
性质求出未知数的值x=a(常数)
下课了!
