解一元一次方程(二)
图片预览




文档简介
(共11张PPT)
3.3 解一元一次方程(二)
—— 去括号(第一课时)
授课人:李老师
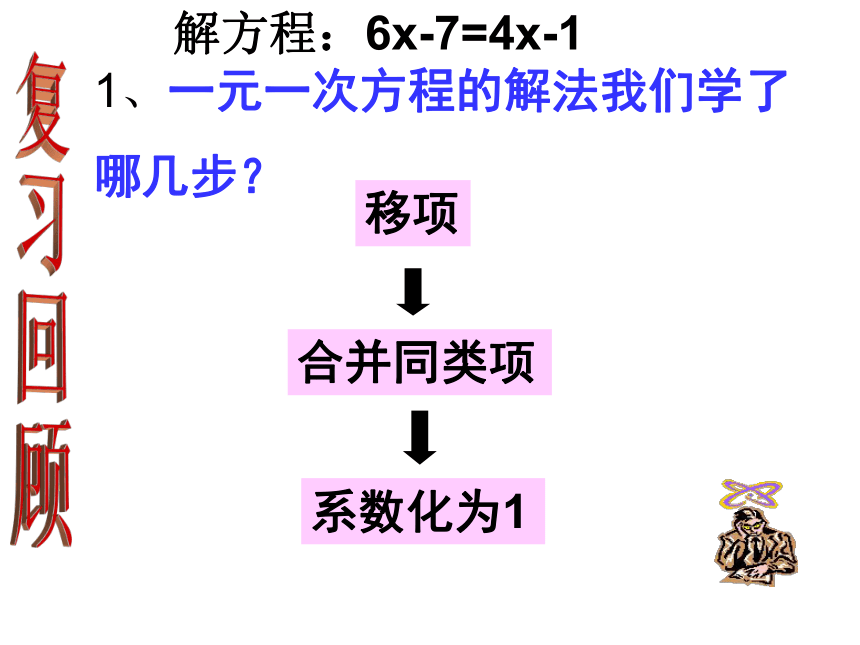
解方程:6x-7=4x-1 1、一元一次方程的解法我们学了
哪几步?
移项
合并同类项
系数化为1
2、移项,合并同类项,系数化为1, 要注意什么?
②合并同类项时,只是把同类项的系数相加作为所得项的系数,字母部分不变。
③系数化为1,也就是说方程两边同时除以未知数前面的系数。
①移项时要变号。(变成相反数)
我们在方程6x-7=4x-1后加上一个括号得6x-7=4(x-1)会解吗?
在前面再加上一个负号得6x-7=-4(x-1)会吗?
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
分析:若设上半年每月平均用电x度,
则下半年每月平均用电 度
上半年共用电 度,
下半年共用电 度
因为全年共用了15万度电,
所以,可列方程 。
(x-2000)
6(x-2000)
6x
6x+ 6(x-2000)=150000
6x+ 6(x-2000)=150000
问题:这个方程有什么特点,和以前我们学过的方程有什么不同?怎样使这个方程向x=a转化?
去括号
移项
合并同类项
系数化为1
6x+ 6(x-2000)=150000
去括号,得
6x + 6x - 12000 = 150000
移项,得
6x + 6x = 150000 + 12000
合并同类项,得
12x = 162000
x = 13500
系数化为1,得
注:方程中有带括号的式子时,去括号是常用的化简步骤。
例1.
解方程:3x - 7(x-1) = 3 - 2(x+3)
例2.
解方程:3(5x-1)- 2(3x+2)=6(x-1)+2
试一试:解下列方程 (练习97页)
1、 4x + 3(2X-3) = 12- (x+4)
2、6( x - 4) + 2x = 7-( x - 1)
思考题:
3x-2[3(x-1)-2(x+2)]=3(18-x)
本节课学习了什么?
本节课学习了用去括号的方法解一元一次方程。
需要注意的是:
(1)如果括号外的因数是负数时,去括号后,原括号内各项的符号要改变符号;
(2)乘数与括号内多项式相乘时,乘数应乘括号内的每一项,不要漏乘。
3.3 解一元一次方程(二)
—— 去括号(第一课时)
授课人:李老师
解方程:6x-7=4x-1 1、一元一次方程的解法我们学了
哪几步?
移项
合并同类项
系数化为1
2、移项,合并同类项,系数化为1, 要注意什么?
②合并同类项时,只是把同类项的系数相加作为所得项的系数,字母部分不变。
③系数化为1,也就是说方程两边同时除以未知数前面的系数。
①移项时要变号。(变成相反数)
我们在方程6x-7=4x-1后加上一个括号得6x-7=4(x-1)会解吗?
在前面再加上一个负号得6x-7=-4(x-1)会吗?
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
分析:若设上半年每月平均用电x度,
则下半年每月平均用电 度
上半年共用电 度,
下半年共用电 度
因为全年共用了15万度电,
所以,可列方程 。
(x-2000)
6(x-2000)
6x
6x+ 6(x-2000)=150000
6x+ 6(x-2000)=150000
问题:这个方程有什么特点,和以前我们学过的方程有什么不同?怎样使这个方程向x=a转化?
去括号
移项
合并同类项
系数化为1
6x+ 6(x-2000)=150000
去括号,得
6x + 6x - 12000 = 150000
移项,得
6x + 6x = 150000 + 12000
合并同类项,得
12x = 162000
x = 13500
系数化为1,得
注:方程中有带括号的式子时,去括号是常用的化简步骤。
例1.
解方程:3x - 7(x-1) = 3 - 2(x+3)
例2.
解方程:3(5x-1)- 2(3x+2)=6(x-1)+2
试一试:解下列方程 (练习97页)
1、 4x + 3(2X-3) = 12- (x+4)
2、6( x - 4) + 2x = 7-( x - 1)
思考题:
3x-2[3(x-1)-2(x+2)]=3(18-x)
本节课学习了什么?
本节课学习了用去括号的方法解一元一次方程。
需要注意的是:
(1)如果括号外的因数是负数时,去括号后,原括号内各项的符号要改变符号;
(2)乘数与括号内多项式相乘时,乘数应乘括号内的每一项,不要漏乘。
