人教版八年级上册数学导学案:第十二章《全等三角形全章复习》(无答案)
文档属性
| 名称 | 人教版八年级上册数学导学案:第十二章《全等三角形全章复习》(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 192.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-06 00:00:00 | ||
图片预览


文档简介
《全等三角形全章复习》导学案
学习目标:
系统理解本章知识点:全等三角形的判定、性质。角平分线的性质定理和判定定理;
能较熟练地运用本章知识解决问题。
学习重点:
对本章四个知识点及其关系的准确理解及熟练运用。
学习难点:
对本章四个知识点及其关系的准确理解。
导学过程:
【全等三角形的性质知识点1】
全等三角形的对应___相等,对应___相等,_____相等,______相等,对应边上的_____相等,对应角的______相等,对应边上的_____相等。
例、如图所示,图中是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到,如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分面积为______
练习:如图,A、D、E三点在同一直线上,且,
(1)试说明BD=DE+CE;
(2)满足什么条件时,BD∥CE?
【全等三角形的判定知识点】
1.三角形全等的判定方法:_________________________________
2.直角三角形全等的判定方法:_______________________________________
3.有两种不能用来判定全的的方法是:___________________________________
4.判定三角形全等的思路:______________________________________________
5.三角形全等证明过程的书写格式________________________________________
例1:已知在中,AD为的中线,且AB=8cm,AC=5cm,如图所示,求中线AD的取值范围。
例2:如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有____________________(把你认为正确的序号都填上)。
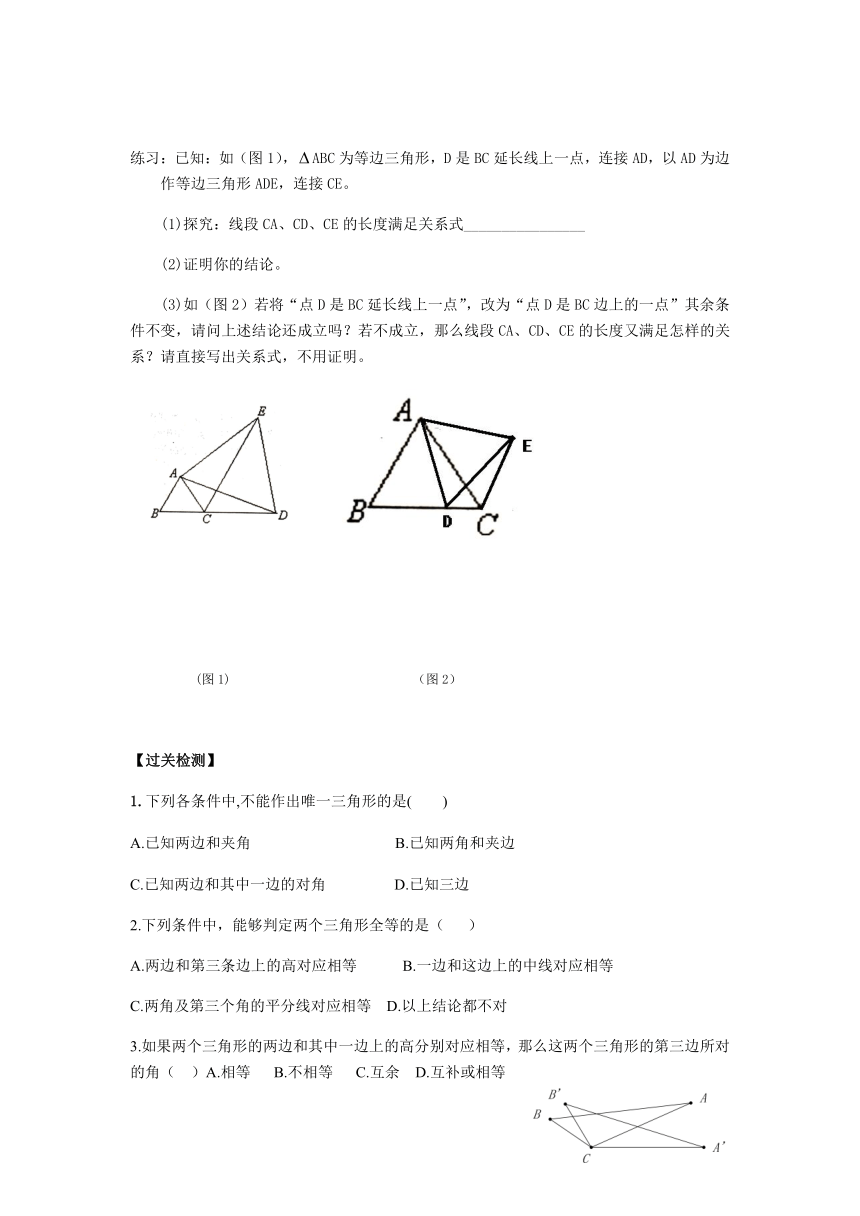
练习:已知:如(图1),ABC为等边三角形,D是BC延长线上一点,连接AD,以AD为边作等边三角形ADE,连接CE。
(1)探究:线段CA、CD、CE的长度满足关系式________________
(2)证明你的结论。
(3)如(图2)若将“点D是BC延长线上一点”,改为“点D是BC边上的一点”其余条件不变,请问上述结论还成立吗?若不成立,那么线段CA、CD、CE的长度又满足怎样的关系?请直接写出关系式,不用证明。
(图1)
(图2)
【过关检测】
1.下列各条件中,不能作出唯一三角形的是(
)
A.已知两边和夹角
B.已知两角和夹边
C.已知两边和其中一边的对角
D.已知三边
2.下列条件中,能够判定两个三角形全等的是(
)
A.两边和第三条边上的高对应相等
B.一边和这边上的中线对应相等
C.两角及第三个角的平分线对应相等
D.以上结论都不对
3.如果两个三角形的两边和其中一边上的高分别对应相等,那么这两个三角形的第三边所对的角(
)A.相等
B.不相等
C.互余
D.互补或相等
4.如图,从下列四个条件:①②
③④,任取三个为条件,余下一个为结论,则最多可以构成正确的结论的个数是(
)
A.1个
B.2个
C.3个
D.4个
5.
如图,,请你添加一个条件:
,使(只添一个即可).
6.
等边△ABC中,BD=CE,AD与BE相交于点F,则∠AFE的度数为_______.
【角平分线知识点】
1.角平分线的画法____________________________________
2.角平分线的性质_________________________________________________
3.角平分线的判定__________________________________________________
4.到三角形三边距离相等的点是________________________________的交点。
例1、
如图已知AB=AC,BD=CD,DE⊥AB交AB于E,DF⊥AC交AC于F。求证:DE=DF。
例2、如图,已知在ABC中,BD=DC,∠1=∠2,求证:AD平分∠BAC。
练习:如图,P为内一点,已知PA=PB,,求证:。
【过关检测】
1、如图,已知在中,,AB=AC,CD平分,DE⊥BC于E,若BC=15cm,则的周长为_____________
2、△ABC中,AD是它的角平分线。且BD=CD,DE、DF分别垂直AB、AC。垂足分别为E、F。求证:EB=FC
3、如图,已知相交直线AB和CD及另一直线MN.如果要在MN上找出与AB、CD距离相等的点,方法是
,这样的点至少有
个,最多有
个.为什么呢?
学习目标:
系统理解本章知识点:全等三角形的判定、性质。角平分线的性质定理和判定定理;
能较熟练地运用本章知识解决问题。
学习重点:
对本章四个知识点及其关系的准确理解及熟练运用。
学习难点:
对本章四个知识点及其关系的准确理解。
导学过程:
【全等三角形的性质知识点1】
全等三角形的对应___相等,对应___相等,_____相等,______相等,对应边上的_____相等,对应角的______相等,对应边上的_____相等。
例、如图所示,图中是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到,如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分面积为______
练习:如图,A、D、E三点在同一直线上,且,
(1)试说明BD=DE+CE;
(2)满足什么条件时,BD∥CE?
【全等三角形的判定知识点】
1.三角形全等的判定方法:_________________________________
2.直角三角形全等的判定方法:_______________________________________
3.有两种不能用来判定全的的方法是:___________________________________
4.判定三角形全等的思路:______________________________________________
5.三角形全等证明过程的书写格式________________________________________
例1:已知在中,AD为的中线,且AB=8cm,AC=5cm,如图所示,求中线AD的取值范围。
例2:如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有____________________(把你认为正确的序号都填上)。
练习:已知:如(图1),ABC为等边三角形,D是BC延长线上一点,连接AD,以AD为边作等边三角形ADE,连接CE。
(1)探究:线段CA、CD、CE的长度满足关系式________________
(2)证明你的结论。
(3)如(图2)若将“点D是BC延长线上一点”,改为“点D是BC边上的一点”其余条件不变,请问上述结论还成立吗?若不成立,那么线段CA、CD、CE的长度又满足怎样的关系?请直接写出关系式,不用证明。
(图1)
(图2)
【过关检测】
1.下列各条件中,不能作出唯一三角形的是(
)
A.已知两边和夹角
B.已知两角和夹边
C.已知两边和其中一边的对角
D.已知三边
2.下列条件中,能够判定两个三角形全等的是(
)
A.两边和第三条边上的高对应相等
B.一边和这边上的中线对应相等
C.两角及第三个角的平分线对应相等
D.以上结论都不对
3.如果两个三角形的两边和其中一边上的高分别对应相等,那么这两个三角形的第三边所对的角(
)A.相等
B.不相等
C.互余
D.互补或相等
4.如图,从下列四个条件:①②
③④,任取三个为条件,余下一个为结论,则最多可以构成正确的结论的个数是(
)
A.1个
B.2个
C.3个
D.4个
5.
如图,,请你添加一个条件:
,使(只添一个即可).
6.
等边△ABC中,BD=CE,AD与BE相交于点F,则∠AFE的度数为_______.
【角平分线知识点】
1.角平分线的画法____________________________________
2.角平分线的性质_________________________________________________
3.角平分线的判定__________________________________________________
4.到三角形三边距离相等的点是________________________________的交点。
例1、
如图已知AB=AC,BD=CD,DE⊥AB交AB于E,DF⊥AC交AC于F。求证:DE=DF。
例2、如图,已知在ABC中,BD=DC,∠1=∠2,求证:AD平分∠BAC。
练习:如图,P为内一点,已知PA=PB,,求证:。
【过关检测】
1、如图,已知在中,,AB=AC,CD平分,DE⊥BC于E,若BC=15cm,则的周长为_____________
2、△ABC中,AD是它的角平分线。且BD=CD,DE、DF分别垂直AB、AC。垂足分别为E、F。求证:EB=FC
3、如图,已知相交直线AB和CD及另一直线MN.如果要在MN上找出与AB、CD距离相等的点,方法是
,这样的点至少有
个,最多有
个.为什么呢?
