人教A版高中数学必修二3.3.3点到直线的距离(17张ppt)
文档属性
| 名称 | 人教A版高中数学必修二3.3.3点到直线的距离(17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 189.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 11:30:38 | ||
图片预览


文档简介
点到直线的距离
新课导入
点到直线的距离
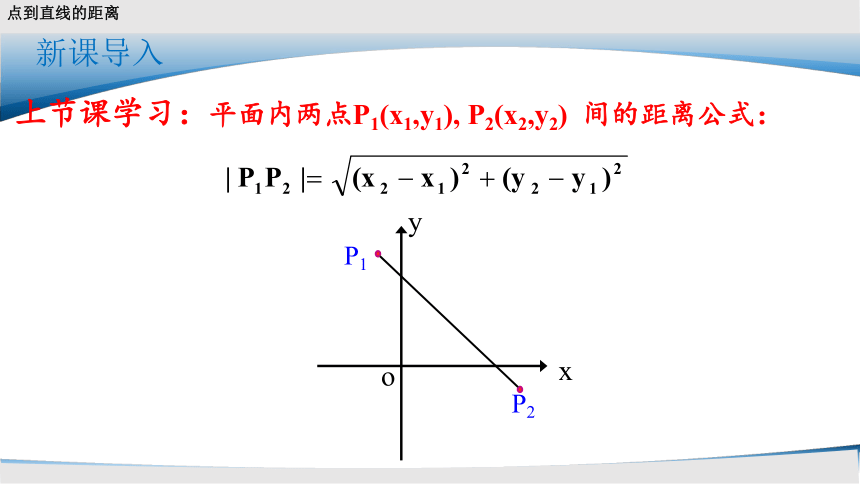
上节课学面内两点P1(x1,y1),
P2(x2,y2)
间的距离公式:
y
x
o
P2
P1
兵团第十二师高级中学
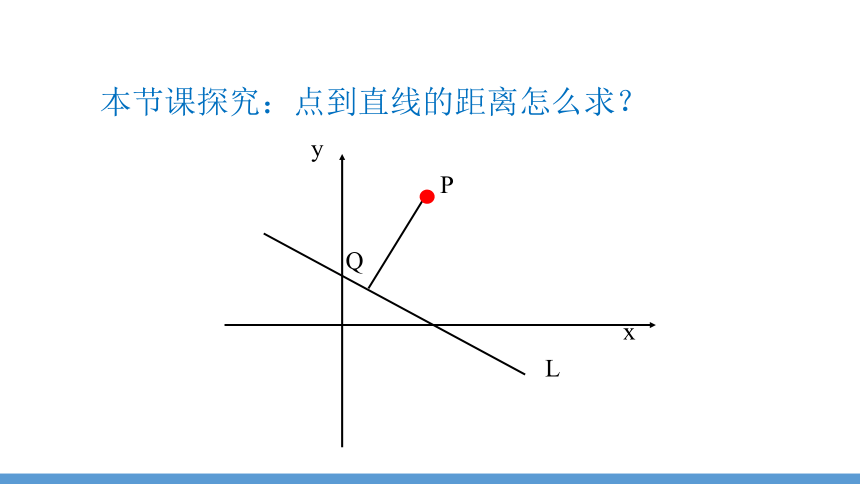
本节课探究:点到直线的距离怎么求?
L
x
P
Q
y
兵团第十二师高级中学
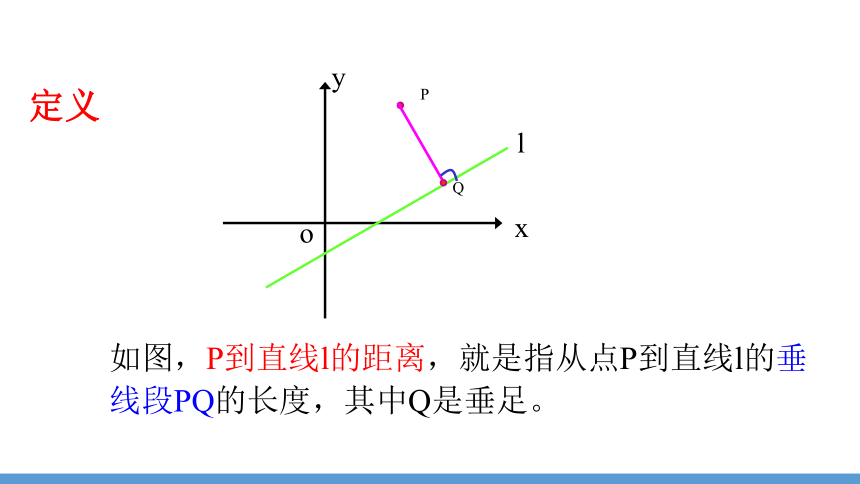
如图,P到直线l的距离,就是指从点P到直线l的垂线段PQ的长度,其中Q是垂足。
Q
P
y
x
o
l
定义
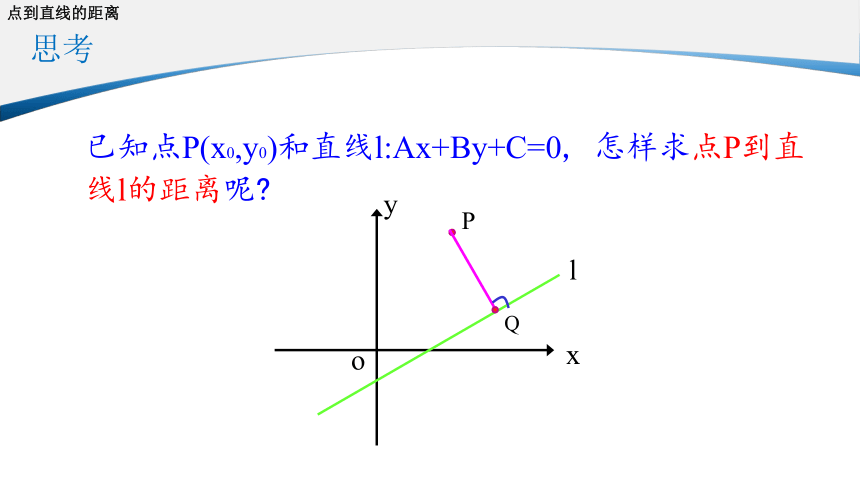
思考
已知点P(x0,y0)和直线l:Ax+By+C=0,
怎样求点P到直线l的距离呢?
点到直线的距离
Q
P
y
x
o
l
兵团第十二师高级中学
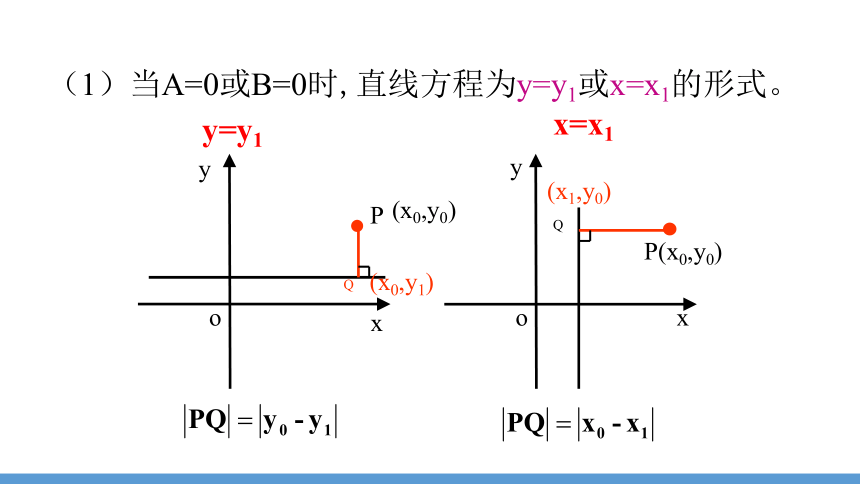
(1)当A=0或B=0时,直线方程为y=y1或x=x1的形式。
x=x1
y=y1
Q
Q
x
y
o
P(x0,y0)
y
o
(x0,y0)
x
P
(x0,y1)
(x1,y0)
兵团第十二师高级中学
(2)A≠0,B
≠0时
[思路一]
利用两点间距离公式
过点P作l1⊥l
,垂足为Q,则
|PQ|
就是点P
到
直线l
的距离,
依题意
l1:
Bx-Ay-Bx0+Ay0=0
Ax+By+C=0
B
x-Ay-Bx0+Ay0=0
Q(x,
y)满足:
P
y
x
o
l
Q
l1
兵团第十二师高级中学
P
y
x
o
l
Q
l1
兵团第十二师高级中学
(2)A≠0,B
≠0时
[思路二]
构造直角三角形求其高
S
R
Q
x
y
P(x0,y0)
O
L:Ax+By+C=0
得:
由P
(x0
,
y0)及l:
Ax+By+C=0
设S(x1,
y0),R(x0,
y2),则
Ax1+By0+C=0
Ax0+By2+C=0
兵团第十二师高级中学
S
R
Q
x
y
P(x0,y0)
O
L:Ax+By+C=0
设|PQ|=d,由三角形面积公式可得:
d×|RS|=|PR|×|PS|
兵团第十二师高级中学
点P
(x0
,
y0)到直线
l:
Ax+By+C=0的距离为:
Q
P
y
x
o
l
思考
点到直线的距离
P
Q
x
y
0
L
当A=0时,上述公式是否成立?
与公式
比较,符合公式。
思考
点到直线的距离
当B=0时,上述公式是否成立?
P
Q
x
y
0
L
与公式
比较,符合公式。
例5
求点P(
-1,2
)到下列直线的距离:
⑴
2x+y-10
=0
⑵
3x=2
⑵
因为直线3x=2平行于y轴,
所以
⑴
解:
点到直线的距离
课堂小结
点到直线的距离
点到直线的距离公式
Q
P
y
x
0
l
课堂小结
点到直线的距离
点到直线的距离公式
Q
P
y
x
0
l
课后作业
点到直线的距离
1.求原点到下列直线的距离:
(1)
3x+2y-26=0
(2)
y=x
2.(1)P(-2,3)到直线y=
-2的距离是________
(2)P(-1,1)到直线3x=
2的距离是_________
(3)P(2,-3)到直线x+2y+4=
0的距离是_______
3.习题3.3A组9;B组2,4.
新课导入
点到直线的距离
上节课学面内两点P1(x1,y1),
P2(x2,y2)
间的距离公式:
y
x
o
P2
P1
兵团第十二师高级中学
本节课探究:点到直线的距离怎么求?
L
x
P
Q
y
兵团第十二师高级中学
如图,P到直线l的距离,就是指从点P到直线l的垂线段PQ的长度,其中Q是垂足。
Q
P
y
x
o
l
定义
思考
已知点P(x0,y0)和直线l:Ax+By+C=0,
怎样求点P到直线l的距离呢?
点到直线的距离
Q
P
y
x
o
l
兵团第十二师高级中学
(1)当A=0或B=0时,直线方程为y=y1或x=x1的形式。
x=x1
y=y1
Q
Q
x
y
o
P(x0,y0)
y
o
(x0,y0)
x
P
(x0,y1)
(x1,y0)
兵团第十二师高级中学
(2)A≠0,B
≠0时
[思路一]
利用两点间距离公式
过点P作l1⊥l
,垂足为Q,则
|PQ|
就是点P
到
直线l
的距离,
依题意
l1:
Bx-Ay-Bx0+Ay0=0
Ax+By+C=0
B
x-Ay-Bx0+Ay0=0
Q(x,
y)满足:
P
y
x
o
l
Q
l1
兵团第十二师高级中学
P
y
x
o
l
Q
l1
兵团第十二师高级中学
(2)A≠0,B
≠0时
[思路二]
构造直角三角形求其高
S
R
Q
x
y
P(x0,y0)
O
L:Ax+By+C=0
得:
由P
(x0
,
y0)及l:
Ax+By+C=0
设S(x1,
y0),R(x0,
y2),则
Ax1+By0+C=0
Ax0+By2+C=0
兵团第十二师高级中学
S
R
Q
x
y
P(x0,y0)
O
L:Ax+By+C=0
设|PQ|=d,由三角形面积公式可得:
d×|RS|=|PR|×|PS|
兵团第十二师高级中学
点P
(x0
,
y0)到直线
l:
Ax+By+C=0的距离为:
Q
P
y
x
o
l
思考
点到直线的距离
P
Q
x
y
0
L
当A=0时,上述公式是否成立?
与公式
比较,符合公式。
思考
点到直线的距离
当B=0时,上述公式是否成立?
P
Q
x
y
0
L
与公式
比较,符合公式。
例5
求点P(
-1,2
)到下列直线的距离:
⑴
2x+y-10
=0
⑵
3x=2
⑵
因为直线3x=2平行于y轴,
所以
⑴
解:
点到直线的距离
课堂小结
点到直线的距离
点到直线的距离公式
Q
P
y
x
0
l
课堂小结
点到直线的距离
点到直线的距离公式
Q
P
y
x
0
l
课后作业
点到直线的距离
1.求原点到下列直线的距离:
(1)
3x+2y-26=0
(2)
y=x
2.(1)P(-2,3)到直线y=
-2的距离是________
(2)P(-1,1)到直线3x=
2的距离是_________
(3)P(2,-3)到直线x+2y+4=
0的距离是_______
3.习题3.3A组9;B组2,4.
