第二章 实数 回顾与思考 课件(共27张PPT)
文档属性
| 名称 | 第二章 实数 回顾与思考 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 16:10:03 | ||
图片预览





文档简介
第二章
实数
总复习
2020年秋北师大版八年级上册
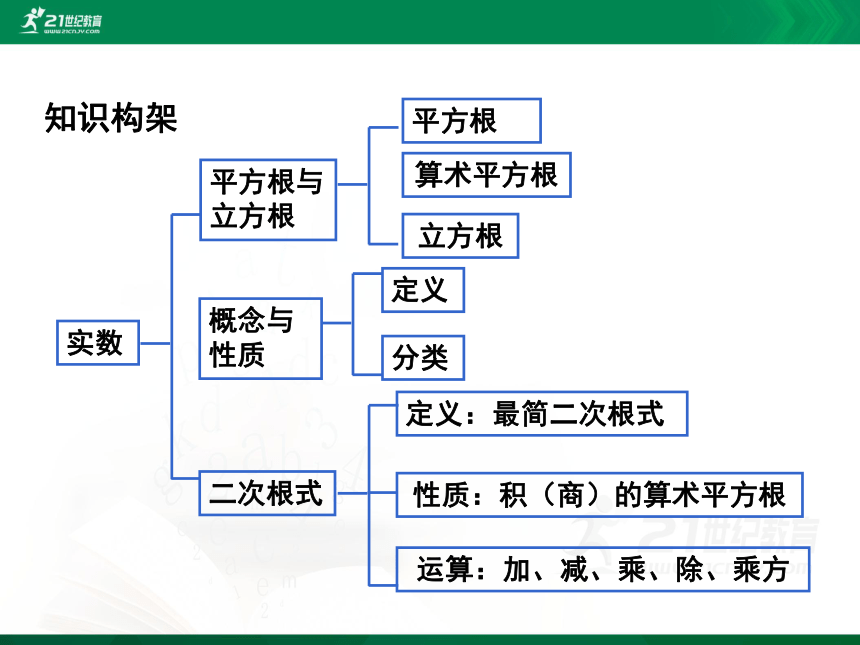
平方根与立方根
二次根式
实数
平方根
算术平方根
定义:最简二次根式
性质:积(商)的算术平方根
运算:加、减、乘、除、乘方
立方根
概念与性质
定义
分类
知识构架
(一)无理数
无限不循环小数叫无理数.
无理数常见的三种类型:
(1)含π的数,如2π;
(2)有根号,但开不尽方的数;
(3)特殊的数,0.585885888588885…(两个5之间的8的个数逐渐增加1)
一、知识点回顾
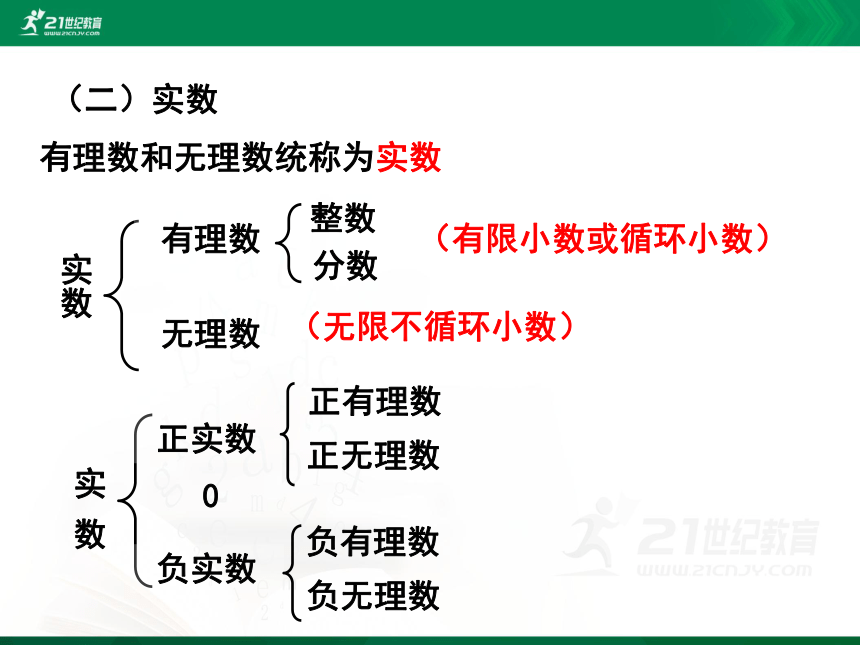
(二)实数
有理数
实数
分数
无理数
整数
(有限小数或循环小数)
(无限不循环小数)
有理数和无理数统称为实数
正实数
实 数
0
负实数
正有理数
正无理数
负有理数
负无理数
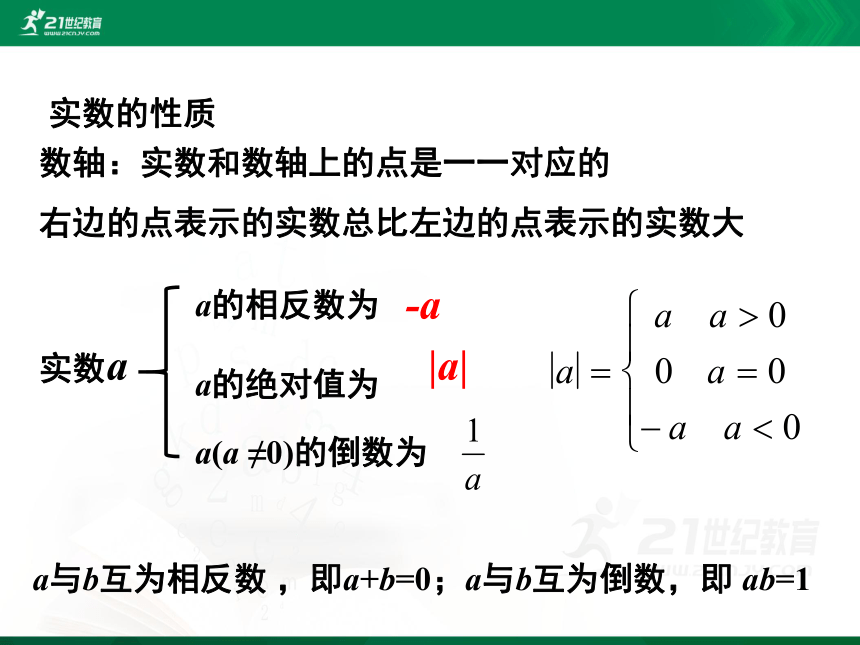
实数的性质
实数a
a的相反数为
a的绝对值为
a(a ≠0)的倒数为
-a
|a|
数轴:实数和数轴上的点是一一对应的
右边的点表示的实数总比左边的点表示的实数大
a与b互为相反数 ,即a+b=0;a与b互为倒数,即 ab=1
算术平方根的意义:
(a≥0)
算术平方根具有双重非负性
非负数
≥0
正数a的正的平方根,叫做这个正数的算术平方根
0的算术平方根是0 ,即
(三)算术平方根
一般地,如果一个数x的平方等于a,即x2= a,那么这个数叫做a 的平方根(二次方根).
(四)平方根
记作:
( 2可以省略)
一个正数有两个平方根;0只有一个平方根,它是0本身;负数没有平方根。
(只有非负数才有平方根)
(算术平方根)
一个正数a的两个平方根互为相反数
正平方根:
负平方根:
如果一个数x的立方等于a ,即 x3= a, 那么这个数x就叫做a的立方根(也叫做三次方根)
记作:
(3是根指数,不能省略)
(五)立方根
立方根的性质
(同号性、唯一性)
(1)正数的立方根有一个,是正数;
(2)0的立方根有一个,是0;
(3)负数的立方根有一个,是负数。
每个数a都有一个立方根
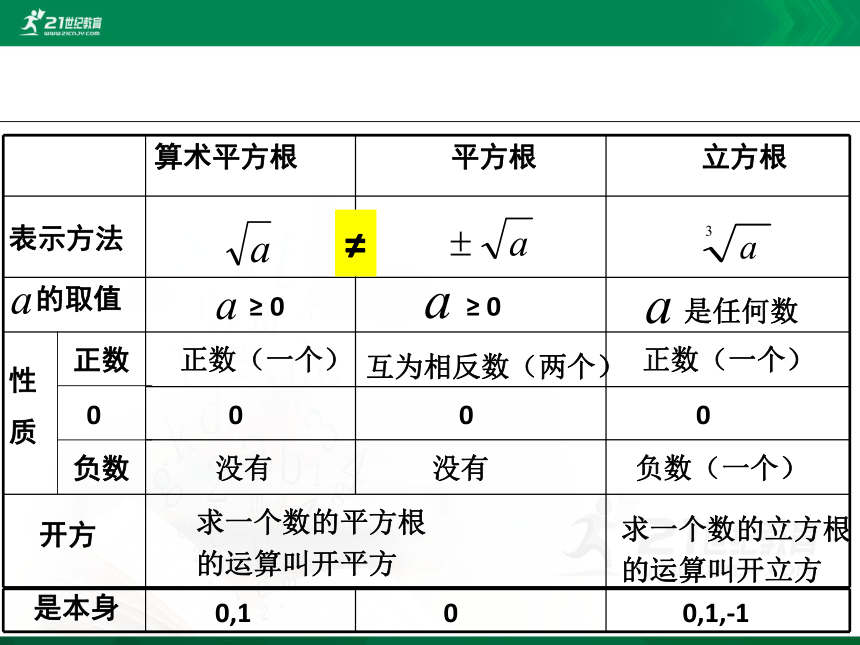
算术平方根
平方根
立方根
表示方法
的取值
性
质
≥ 0
开方
≥ 0
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
≠
是本身
0,1
0
0,1,-1
是任何数
平方根与立方根的性质
(六)估算
(1)估算无理数的大小
(2)确定整数部分与小数部分
(3)比较大小:平方比较法,夹逼估算法
1.定义:
形如 的式子叫做二次根式,
2.性质:
⑴积的算术平方根:
等于算术平方根的积;
⑵商的算术平方根:
等于算术平方根的商;
其中a叫做被开方数.
(七)二次根式
3.最简二次根式 :
满足以下三个条件的二次根式叫最简二次根式 :
⑴被开方数不能含有开得尽方的因数或因式;
⑵被开方数不能含有分母;
⑶分母不能含有根号.
注意:
二次根式的化简与运算,最后结果应化成最简二次根式.
4.二次根式的运算 :
⑴同类二次根式的加减
(类似合并同类项)
⑵二次根式的乘法 :
⑶二次根式的除法 :
(4)二次根式的乘方 :
注意:平方差公式与完全平方公式的运用!
在下列各数中,无理数的个数为( )
3.14,0,-π ,0.181818… ,
0.101 001 000 1…(相邻两个1之间0的个数逐次加1)
A. 4个 B. 3个
C. 2个 D. 1个
C
二、典例精讲
2.一个正数的平方根分别是x+2和2x-5,则x=______.
二、典例精讲
X=1
3. 的平方根为_________.
±2
4.下列计算正确的是( )
A
5. 的值是( )
A. 1 B. -1 C. 3 D. -3
B
二、典例精讲
6.若x使(x-1)2=4成立,则x的值是( )
A.3 B.-1 C.3或-1 D. ±2
C
7. 若实数x,y满足(2x+3)2+|9-4y|=0,则xy的立方根为______.
8. 如图,数轴上的点A,B,O,C,D分别表示数
-2,-1,0,1,2,则表示数 的点P应落在( )
A. 线段AB上 B. 线段BO上
C. 线段OC上 D. 线段CD上
B
二、典例精讲
A
二、典例精讲
10.若式子 有意义,则x的取值范围是________.
x≤2
11. 若 ,则实数a在数轴上的对应点一定在( )
A. 原点左侧 B. 原点右侧
C. 原点或原点左侧 D. 原点或原点右侧
C
二、典例精讲
12. 若x,y都是实数,且y = ,
求x+3y的立方根.
解:因为y=
所以x-3≥0,且3-x≥0.
解得x=3.
将x=3代入y= 得y=8.
所以x+3y=3+3×8=27.
所以x+3y的立方根即27的立方根为3.
二、典例精讲
13. 已知2a-1的平方根是±3,4是3a+b-1的算术平方根,求 的值.
解:因为2a-1的平方根是±3,所以2a-1=9.
所以a=5.
又因为4是3a+b-1的算术平方根,所以3a+b-1=16.
将a=5代入3a+b-1=16,得b=2.
所以a+2b=5+2×2=9.
所以 = =3.
二、典例精讲
14. 化简:
二、典例精讲
解:原式
15.实数a,b在数轴上的位置如图,化简
解:因为a<0<b,
所以原式=|a|-|b|-|a-b|
=-a-b+a-b
=-2b.
二、典例精讲
16.先化简,再求值
二、典例精讲
谢谢
实数
总复习
2020年秋北师大版八年级上册
平方根与立方根
二次根式
实数
平方根
算术平方根
定义:最简二次根式
性质:积(商)的算术平方根
运算:加、减、乘、除、乘方
立方根
概念与性质
定义
分类
知识构架
(一)无理数
无限不循环小数叫无理数.
无理数常见的三种类型:
(1)含π的数,如2π;
(2)有根号,但开不尽方的数;
(3)特殊的数,0.585885888588885…(两个5之间的8的个数逐渐增加1)
一、知识点回顾
(二)实数
有理数
实数
分数
无理数
整数
(有限小数或循环小数)
(无限不循环小数)
有理数和无理数统称为实数
正实数
实 数
0
负实数
正有理数
正无理数
负有理数
负无理数
实数的性质
实数a
a的相反数为
a的绝对值为
a(a ≠0)的倒数为
-a
|a|
数轴:实数和数轴上的点是一一对应的
右边的点表示的实数总比左边的点表示的实数大
a与b互为相反数 ,即a+b=0;a与b互为倒数,即 ab=1
算术平方根的意义:
(a≥0)
算术平方根具有双重非负性
非负数
≥0
正数a的正的平方根,叫做这个正数的算术平方根
0的算术平方根是0 ,即
(三)算术平方根
一般地,如果一个数x的平方等于a,即x2= a,那么这个数叫做a 的平方根(二次方根).
(四)平方根
记作:
( 2可以省略)
一个正数有两个平方根;0只有一个平方根,它是0本身;负数没有平方根。
(只有非负数才有平方根)
(算术平方根)
一个正数a的两个平方根互为相反数
正平方根:
负平方根:
如果一个数x的立方等于a ,即 x3= a, 那么这个数x就叫做a的立方根(也叫做三次方根)
记作:
(3是根指数,不能省略)
(五)立方根
立方根的性质
(同号性、唯一性)
(1)正数的立方根有一个,是正数;
(2)0的立方根有一个,是0;
(3)负数的立方根有一个,是负数。
每个数a都有一个立方根
算术平方根
平方根
立方根
表示方法
的取值
性
质
≥ 0
开方
≥ 0
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
≠
是本身
0,1
0
0,1,-1
是任何数
平方根与立方根的性质
(六)估算
(1)估算无理数的大小
(2)确定整数部分与小数部分
(3)比较大小:平方比较法,夹逼估算法
1.定义:
形如 的式子叫做二次根式,
2.性质:
⑴积的算术平方根:
等于算术平方根的积;
⑵商的算术平方根:
等于算术平方根的商;
其中a叫做被开方数.
(七)二次根式
3.最简二次根式 :
满足以下三个条件的二次根式叫最简二次根式 :
⑴被开方数不能含有开得尽方的因数或因式;
⑵被开方数不能含有分母;
⑶分母不能含有根号.
注意:
二次根式的化简与运算,最后结果应化成最简二次根式.
4.二次根式的运算 :
⑴同类二次根式的加减
(类似合并同类项)
⑵二次根式的乘法 :
⑶二次根式的除法 :
(4)二次根式的乘方 :
注意:平方差公式与完全平方公式的运用!
在下列各数中,无理数的个数为( )
3.14,0,-π ,0.181818… ,
0.101 001 000 1…(相邻两个1之间0的个数逐次加1)
A. 4个 B. 3个
C. 2个 D. 1个
C
二、典例精讲
2.一个正数的平方根分别是x+2和2x-5,则x=______.
二、典例精讲
X=1
3. 的平方根为_________.
±2
4.下列计算正确的是( )
A
5. 的值是( )
A. 1 B. -1 C. 3 D. -3
B
二、典例精讲
6.若x使(x-1)2=4成立,则x的值是( )
A.3 B.-1 C.3或-1 D. ±2
C
7. 若实数x,y满足(2x+3)2+|9-4y|=0,则xy的立方根为______.
8. 如图,数轴上的点A,B,O,C,D分别表示数
-2,-1,0,1,2,则表示数 的点P应落在( )
A. 线段AB上 B. 线段BO上
C. 线段OC上 D. 线段CD上
B
二、典例精讲
A
二、典例精讲
10.若式子 有意义,则x的取值范围是________.
x≤2
11. 若 ,则实数a在数轴上的对应点一定在( )
A. 原点左侧 B. 原点右侧
C. 原点或原点左侧 D. 原点或原点右侧
C
二、典例精讲
12. 若x,y都是实数,且y = ,
求x+3y的立方根.
解:因为y=
所以x-3≥0,且3-x≥0.
解得x=3.
将x=3代入y= 得y=8.
所以x+3y=3+3×8=27.
所以x+3y的立方根即27的立方根为3.
二、典例精讲
13. 已知2a-1的平方根是±3,4是3a+b-1的算术平方根,求 的值.
解:因为2a-1的平方根是±3,所以2a-1=9.
所以a=5.
又因为4是3a+b-1的算术平方根,所以3a+b-1=16.
将a=5代入3a+b-1=16,得b=2.
所以a+2b=5+2×2=9.
所以 = =3.
二、典例精讲
14. 化简:
二、典例精讲
解:原式
15.实数a,b在数轴上的位置如图,化简
解:因为a<0<b,
所以原式=|a|-|b|-|a-b|
=-a-b+a-b
=-2b.
二、典例精讲
16.先化简,再求值
二、典例精讲
谢谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
