华东师大版数学八年级上册 12. 2.1单项式乘以单项式 课件 (17张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 12. 2.1单项式乘以单项式 课件 (17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 09:57:16 | ||
图片预览






文档简介
(共17张PPT)
华师版八年级上学期精编课件
第十二章
整式的乘除
2.1单项式乘以单项式
dadaozhijian,zhixingheyi.
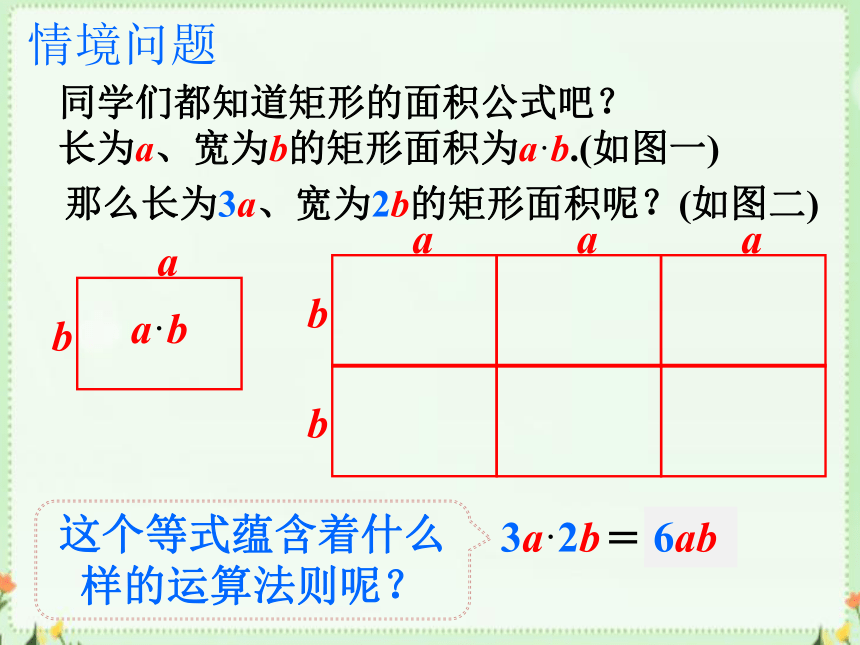
同学们都知道矩形的面积公式吧?
长为a、宽为b的矩形面积为a·b.(如图一)
a
b
3a·2b
=
?
a·b
那么长为3a、宽为2b的矩形面积呢?(如图二)
a
b
a
a
b
6ab
这个等式蕴含着什么样的运算法则呢?
情境问题
1、下列整式中哪些是单项式?哪些是多项式?
单项式:
多项式:
温故知新
2、下列单项式的系数和次数分别是什么?
单项式:
系数:
次数:
1
1
3
1
2
温故知新
3、利用乘法的交换律,结合律计算:
解:原式=
=
=
温故知新
1、同底数幂相乘,底数不变,指数相加。
一般形式:
2、幂的乘方,底数不变,指数相乘。
一般形式:
3、积的乘方等于各因数乘方的积。
一般形式:
am?an=am+n(m、n为正整数)
(am)n=amn(m、n为正整数)
(a?b)n=an?bn(n为正整数)
温故知新
大家试试用乘法交换律、结合律及幂的乘法运算法则计算:
(1)(3×105)×(5×102);(2)2x3·5x2
解:(1)(3×105)×(5×102)
(2)2x3·5x2
=(3×5)×(105×102)
=15×107
=1.5×108
=(2×5)·(x3·x2)
=10x5
探索发现
同理,计算:
(1)3x2y·(-2xy3);(2)(-5a2b3)·(-4b2c)
解:(1)
3x2y·(-2xy3)
(2)(-5a2b3)·(-4b2c)
=[3×(-2)]·(x2·x)·(y·y3)
=-6x3y4
=[(-5)·(-4)]·a2·(b3·b2)·c
=20a2b5c
根据这几道题,尝试总结一下单项式与单项式相乘
的运算法则吧!
探索发现
各单项式的系数相乘;
(axmyp)?(bxn)=ab?xm+nyp
(m、n、p为正整数)
单项式与单项式相乘法则
相同字母的幂按同底数的幂相乘;
只在一个单项式里含有的字母,
连同它的指数作为积的一个因式.
一般形式:
归纳:
1.计算:
(1)(-4a2b5c)?3ab6?(-7b2c3)
(2)(-2×105)(-7×103)(-3×102)
(3)
解:(1)原式=(4×3×7)·a2+1·b5+6+2·c1+3
(2)原式=(-2×7×3)×105+3+2
(3)原式=
=98a3b13c4
=(-42)×1010
=-4.2×1011
剩下的步骤大家一起来完成吧!
例题示范
2.选择题:
(1)下列计算正确的是(
)
A.4a2?2a3=8a6
B.-3a2(-4a)=-12a3
C.(-x)2?(-x)3=x5
D.(-2x2)2?(-0.25x)=-x5
D
(2)若(mx4)?(4xk)=12x12,则m、k的值是(
)
A.m=3,k=3
B.m=3,k=8
C.m=8,k=3
D.m=8,k=8
B
例题示范
3、应用:
卫星绕地球运动的速度约7.9×103米/秒,则卫星绕地球运行3×102秒走过的路程约是多少?(结果用科学记数法表示)
解:
7.9×103
×
3×102
=23.7
×105
=2.37
×106
答:卫星绕地球运行3×102秒走过
的路程约是2.37
×106米。
(1)3m?5m2=
.
(2)(-2.5x)·(-4x)=
.
(3)x2yz?xyz3=
.
(4)(-2y)·(3xy5)=
.
(5)(-2x)3(-4x2)=
.
(6)xm+1y·6xym-1=
.
(7)(2×105)(2×105)=
.
(8)(-5an+1b)·(-2a)=
.
(9)(-xy2z3)4
·(-x2y)3=
.
(10)(4×105)·(5×106)·(3×104)=
.
(11)(
)?(-3x2y)=15x4y2.
快速抢答
单项式与单项式相乘的几何意义
3a·2b可以看作是长为3a,宽为2b的长
方形的面积,那么x·xy
又怎么理解呢?
3ab·2a呢?还有形如a2·a,2a·b·3c,...
画出示意图.
讨论:
单项式与单项式相乘的几何意义
a
b
a
a
b
a
a
式子a·a表示边长为a的正方形的面积.
式子3a·2b表示长为3a,宽为2b的矩形面积.
2a
b
3c
式子2a·b·3c表示长为2a,宽为b,高为3c的长方体的体积.
1、同底数幂的乘法法则:
先把各因数的系数相乘作为积的系数;
再对相同字母的幂按同底数的幂相乘;
只出现了一次的字母连同指数作为积的一个因式.
2、注意问题:
①首先确定积的符号;
②不要漏掉单独出现的字母及其指数.
知识小结
一、基础巩固:
P26练习1—3题;P29习题12.2第1、2题.
二、综合提高:
1、一个长方体的长、宽都是3×102cm,高为宽的4倍,求这个长方体的体积。(结果用科学记数法表示)
2、已知-2x3m+1y2n与4xn-6y-3-m的积是-x4y的同类项,
求m、n的值.
课后作业
华师版八年级上学期精编课件
第十二章
整式的乘除
2.1单项式乘以单项式
dadaozhijian,zhixingheyi.
同学们都知道矩形的面积公式吧?
长为a、宽为b的矩形面积为a·b.(如图一)
a
b
3a·2b
=
?
a·b
那么长为3a、宽为2b的矩形面积呢?(如图二)
a
b
a
a
b
6ab
这个等式蕴含着什么样的运算法则呢?
情境问题
1、下列整式中哪些是单项式?哪些是多项式?
单项式:
多项式:
温故知新
2、下列单项式的系数和次数分别是什么?
单项式:
系数:
次数:
1
1
3
1
2
温故知新
3、利用乘法的交换律,结合律计算:
解:原式=
=
=
温故知新
1、同底数幂相乘,底数不变,指数相加。
一般形式:
2、幂的乘方,底数不变,指数相乘。
一般形式:
3、积的乘方等于各因数乘方的积。
一般形式:
am?an=am+n(m、n为正整数)
(am)n=amn(m、n为正整数)
(a?b)n=an?bn(n为正整数)
温故知新
大家试试用乘法交换律、结合律及幂的乘法运算法则计算:
(1)(3×105)×(5×102);(2)2x3·5x2
解:(1)(3×105)×(5×102)
(2)2x3·5x2
=(3×5)×(105×102)
=15×107
=1.5×108
=(2×5)·(x3·x2)
=10x5
探索发现
同理,计算:
(1)3x2y·(-2xy3);(2)(-5a2b3)·(-4b2c)
解:(1)
3x2y·(-2xy3)
(2)(-5a2b3)·(-4b2c)
=[3×(-2)]·(x2·x)·(y·y3)
=-6x3y4
=[(-5)·(-4)]·a2·(b3·b2)·c
=20a2b5c
根据这几道题,尝试总结一下单项式与单项式相乘
的运算法则吧!
探索发现
各单项式的系数相乘;
(axmyp)?(bxn)=ab?xm+nyp
(m、n、p为正整数)
单项式与单项式相乘法则
相同字母的幂按同底数的幂相乘;
只在一个单项式里含有的字母,
连同它的指数作为积的一个因式.
一般形式:
归纳:
1.计算:
(1)(-4a2b5c)?3ab6?(-7b2c3)
(2)(-2×105)(-7×103)(-3×102)
(3)
解:(1)原式=(4×3×7)·a2+1·b5+6+2·c1+3
(2)原式=(-2×7×3)×105+3+2
(3)原式=
=98a3b13c4
=(-42)×1010
=-4.2×1011
剩下的步骤大家一起来完成吧!
例题示范
2.选择题:
(1)下列计算正确的是(
)
A.4a2?2a3=8a6
B.-3a2(-4a)=-12a3
C.(-x)2?(-x)3=x5
D.(-2x2)2?(-0.25x)=-x5
D
(2)若(mx4)?(4xk)=12x12,则m、k的值是(
)
A.m=3,k=3
B.m=3,k=8
C.m=8,k=3
D.m=8,k=8
B
例题示范
3、应用:
卫星绕地球运动的速度约7.9×103米/秒,则卫星绕地球运行3×102秒走过的路程约是多少?(结果用科学记数法表示)
解:
7.9×103
×
3×102
=23.7
×105
=2.37
×106
答:卫星绕地球运行3×102秒走过
的路程约是2.37
×106米。
(1)3m?5m2=
.
(2)(-2.5x)·(-4x)=
.
(3)x2yz?xyz3=
.
(4)(-2y)·(3xy5)=
.
(5)(-2x)3(-4x2)=
.
(6)xm+1y·6xym-1=
.
(7)(2×105)(2×105)=
.
(8)(-5an+1b)·(-2a)=
.
(9)(-xy2z3)4
·(-x2y)3=
.
(10)(4×105)·(5×106)·(3×104)=
.
(11)(
)?(-3x2y)=15x4y2.
快速抢答
单项式与单项式相乘的几何意义
3a·2b可以看作是长为3a,宽为2b的长
方形的面积,那么x·xy
又怎么理解呢?
3ab·2a呢?还有形如a2·a,2a·b·3c,...
画出示意图.
讨论:
单项式与单项式相乘的几何意义
a
b
a
a
b
a
a
式子a·a表示边长为a的正方形的面积.
式子3a·2b表示长为3a,宽为2b的矩形面积.
2a
b
3c
式子2a·b·3c表示长为2a,宽为b,高为3c的长方体的体积.
1、同底数幂的乘法法则:
先把各因数的系数相乘作为积的系数;
再对相同字母的幂按同底数的幂相乘;
只出现了一次的字母连同指数作为积的一个因式.
2、注意问题:
①首先确定积的符号;
②不要漏掉单独出现的字母及其指数.
知识小结
一、基础巩固:
P26练习1—3题;P29习题12.2第1、2题.
二、综合提高:
1、一个长方体的长、宽都是3×102cm,高为宽的4倍,求这个长方体的体积。(结果用科学记数法表示)
2、已知-2x3m+1y2n与4xn-6y-3-m的积是-x4y的同类项,
求m、n的值.
课后作业
