华东师大版数学八年级上册 12. 3.2两数和(差)的平方 课件(30张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 12. 3.2两数和(差)的平方 课件(30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 10:09:35 | ||
图片预览









文档简介
(共30张PPT)
3.2两数和(差)的平方1
公式的结构特征:
左边是
a2
?
b2
两个二项式的乘积,
(a+b)(a?b)=
即两数和与这两数差的积.
右边是
相同项平方与相反项平方之差,
即这两数的平方差.
温故知新
平方差公式
(a+b)2与(a+2b)2等于多少,而且要用拼图来说明。我到现在还没有结果呢,唉!今天上课又要挨批评了,
怎么办呢?同学们,你们能帮帮我吗?
昨天,数学老师布置了这样一道题目:
情境问题
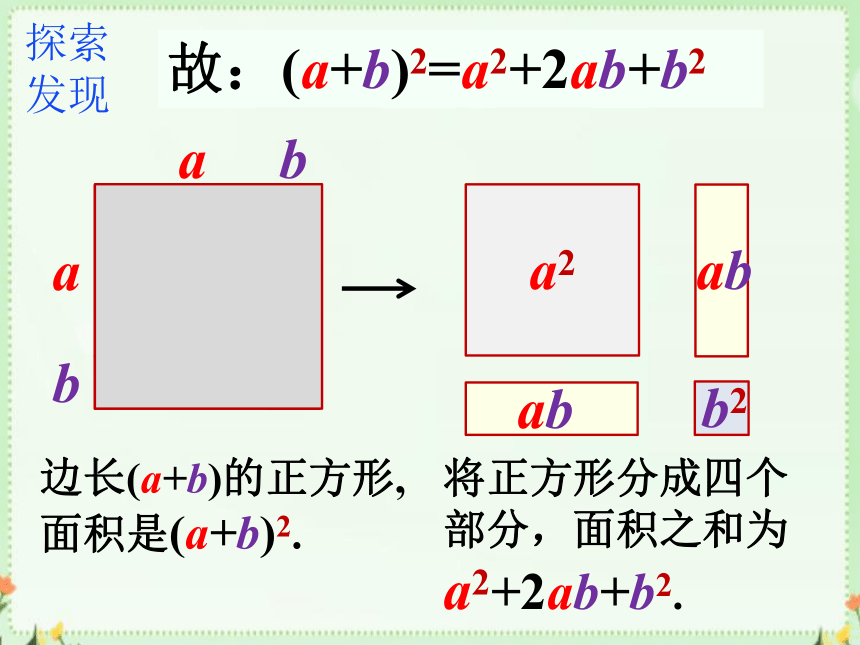
(a+b)2=?
a
a
b
b
a2
ab
ab
b2
边长(a+b)的正方形,面积是(a+b)2.
将正方形分成四个部分,面积之和为a2+2ab+b2.
故:(a+b)2=a2+2ab+b2
探索发现
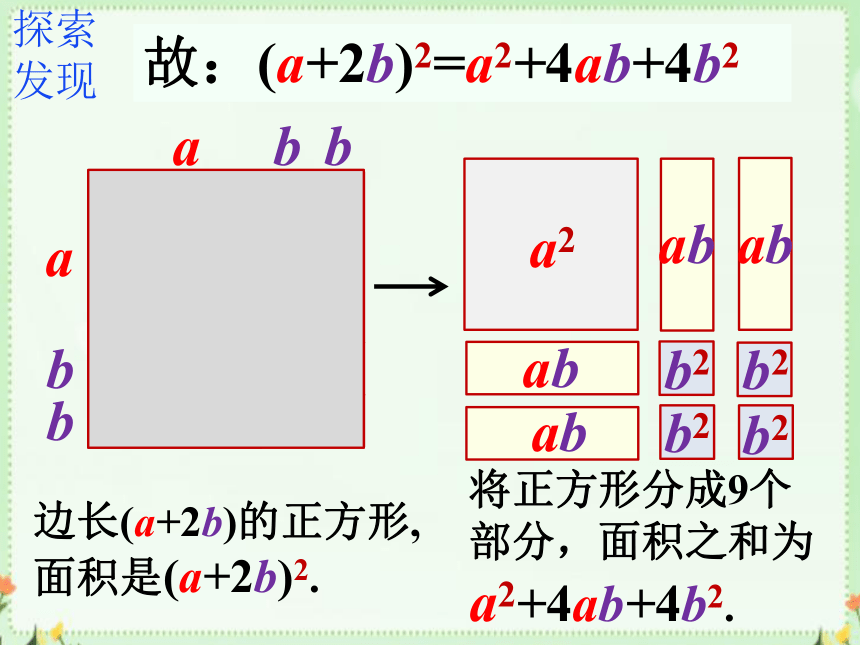
(a+2b)2=?
a2
ab
ab
b2
边长(a+2b)的正方形,面积是(a+2b)2.
将正方形分成9个部分,面积之和为a2+4ab+4b2.
故:(a+2b)2=a2+4ab+4b2
b
a
a
b
b
b
ab
ab
b2
b2
b2
探索发现
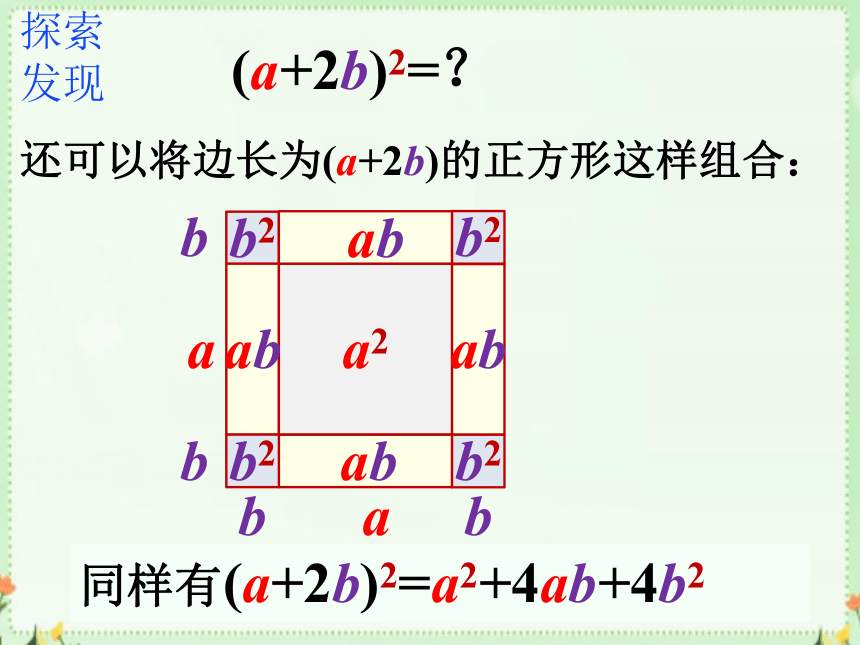
(a+2b)2=?
a2
还可以将边长为(a+2b)的正方形这样组合:
同样有(a+2b)2=a2+4ab+4b2
ab
a
a
b
b
b
b
ab
ab
ab
b2
b2
b2
b2
探索发现
认真观察这两个等式,你能发现什么规律吗?相互交流一下!
(a+b)2
=
a2+2ab+b2
(a+2b)2
=
a2+4ab+4b2
(a+3b)2
=
(3a+b)2
=
(2a+3b)2
=
牛
刀
小
试
a2+6ab+9b2
9a2+6ab+b2
4a2+12ab+9b2
用字母表示为:
这个公式叫两数和的平方公式.
两数和的平方,等于这两数的平方和加上它们积的2倍.
(a+b)2
=
a2+2ab+b2
等式左边是两个数(字母)和的平方.
等式右边可记为:
你平方、我平方、
你我2倍在中央.
(△+□)2
=
△2+2△□+□2
可形象地记为:
认真
观察
理解
抓住
关键
归纳
计算:
(1)(2a+3b)2;
(2)
(2a)2+2×2a?3b+(3b)2
(2)原式=
解:(1)原式=
=
4a2+12ab+9b2
对照公式:(△+□)2
=
△2+2△□+□2
准确找到公式中的△、□.
例题示范
根据两数和的平方公式,你能推导两数差的平方公式吗?
(a-b)2=?
解:
(a-b)2=[a+(-b)]2
将(a-b)理解成省略加号的代数和的形式.
=a2+2?a?(-b)+(-b)2
根据两数和的平方公式
=a2-2ab+b2
探索发现
这个公式叫两数差的平方公式.
两数差的平方,等于这两数的平方和减去它们积的2倍.
(a-b)2
=
a2-2ab+b2
(△-□)2
=
△2-2△□+□2
可形象地记为:
(a+b)2
=
a2+2ab+b2
(a-b)2
=
a2-2ab+b2
我俩有啥不同呢?
归纳
计算:
(1)(2a-3b)2;
(2)
(2a)2-2×2a?3b+(3b)2
(2)原式=
解:(1)原式=
=
4a2-12ab+9b2
对照公式:(△-□)2
=
△2-2△□+□2
准确找到公式中的△、□.
例题示范
(1)根据两数和(差)的平方公式填空:
(-a+b)2=
;
(-a-b)2=
;
(b-a)2
=
;
(b+a)2
=
.
a2-2ab+b2
a2+2ab+b2
b2-2ab+a2
b2+2ab+a2
认真观察,看看你能找到什么规律?相互交流一下
探索发现
(2)根据上述结果可归纳:
当二项式各项的符号相同时,
就用“和”的完全平方式;
当二项式各项的符号不同时,
就用“差”的完全平方式。
(a+b)2
=(-a-b)2=
a2+2ab+b2;
(a-b)2
=(-a+b)2=
a2-2ab+b2
1、两数和(差)的完全平方公式:
2、注意问题:
①必须符合完全平方公式特征的代数式才能用完全平方和(差)公式;
②完全平方和(差)公式可以逆用.
可理解为:两数和(差)的平方,等于这两数的平方和加上(减去)它们积的2倍.
(a+b)2
=(-a-b)2=
a2+2ab+b2;
(a-b)2
=(-a+b)2=
a2-2ab+b2
知识小结
P35练习1—3题;
P37习题12.3第2、3、4题.
课后阅读
P35“读一读”;P37“阅读材料”
课后作业
3.2两数和(差)的平方2
平方差公式:(a+b)(a-b)=
a2-b2
完全平方和(差)公式:
(a+b)2
=(-a-b)2=
a2+2ab+b2;
(a-b)2
=(-a+b)2=
a2-2ab+b2
注意:
必须符合公式特征的代数式才能用公式;
公式可以逆用.
回顾公式
1、下列等式中,不成立的是(
)
A.(3a-b)2=9a2-6ab+b2
B.(a+b-c)2=(c-a-b)2
C.(0.5x-y)2=0.25x2-xy+y2
D.(x+y)(x-y)(x2-y2)=x4-y4
2、判断下列计算是否正确:
(1).(-a2-b)2=a4-2a2b+b4
(
)
(2).(a-c)2=-(c-a)2
(
)
(3).(x3+2y)(x3-2y)=x9-4y2
(
)
(4).(5x-2y)(2y-5x)=-(5x-2y)2
(
)
×
×
×
√
D
练习巩固
4、若(x-y)2=0,则下列等式成立的是(
)
A.
x2+y2=2xy
B.
x2+y2=-2xy
C.
x2+y2=0
D.
x2-y2=0
C
3、下列多项式不能写成一个二项式
的平方的是(
)
A.9a2-6ab+b2
B.4t2+12t+9
C.
x2-4xy-4y2
D.
+m+m2
1
4
A
5、要得到(a-b)2,则a2+3ab+b2应加上(
)
A.
-ab
B.
-3ab
C.
-5ab
D.
-7ab
C
练习巩固
1、完全平方展开式:
例1:(1)如果x2
+ax+121是两个数的
和的平方形式,那么a的值是(
)
A.22
B.11
C.
±22
D.
±11
(x±11)2
=
x2±22x+121
C
(2)如果x2
+6x+k2
恰好是另一个整式的
平方,那么常数k的值是(
)
A.9
B.3
C.
-3
D.
±3
D
(3)如果x2+ax=(x+0.5)2+b,则(
)
A.a=1,b=0.25
B.a=1,b=-0.25
C.a=2,b=0.5
D.a=0,b=-0.5
x2+ax=x2+x+0.25+b
B
例题示范
1、完全平方展开式:
例2:无论x、y取何值时,代数式
x2
+y2
-2x+12y+38的值都是(
)
A.正数
B.负数
C.
零
D.
非负数
x2
+y2
-2x+12y+38
A
=(x2-2x+1)+(y2+12y+36)+1
=(x-1)2+(y+6)2+1
解:
∵(x-1)2≥0,(y+6)2≥0
∴无论x、y取何值,...的值都是正数.
例题示范
2.如何利用完全平方公式简便计算?
例:计算(1)1022
(2)99.82
(3)
解:
(1)原式=
(100+2)2
=
1002+2×100×2+22
=
10000+400+4
=
10404
如果是(-102)2呢?
(2)原式=
(100-0.2)2
=
1002-2×100×0.2+0.22
=
10000-40+0.04
=
9960.04
例题示范
(3)
解:
(3)原式=
如果是
呢?
关键是对底数进行变形:
例题示范
3、完全平方和与完全平方差的转换:
解析:
∵(a+b)2
=
a2+2ab+b2,
(a-b)2
=
a2-2ab+b2
例:填空(1)(a+b)2
=(a-b)2
+
;
(2)(a-b)2=(a+b)2
+
.
∴(a+b)2
+(a-b)2=
2a2+2b2,
(a+b)2
-(a-b)2=
4ab.
4ab
(-4ab)
根据上面的变形,我们能否这样做:
如果已知代数式a+b、a-b、ab、a2+b2中任意两个的值,就可以求出其余的值?
例题示范
1、已知(a+b)2=9,(a-b)2=5,则ab
=
;
练一练:
1
2、已知a+b=-2,ab
=1,则a2+b2=
;
(a+b)2
-(a-b)2=
4ab
(a+b)2=a2+b2+2ab
2
3、已知a+b=1,ab
=-1,则3a2+3b2=
;
a2+b2=(a+b)2-2ab
9
4、已知x+
=6,则x2+
=
;
34
5、已知a-
=2,则a2+
=
.
6
如图,从一块直径为a+b的圆形钢板中,挖去直径分别为a与b的两个圆,求出剩下钢板的面积.
解:由题意得
应用:
答:剩下钢板的面积为0.5πab.
4、完全平方与平方差的综合:
解:
(1)(a-b)2(a+b)2
=
[(a-b)(a+b)]2
例:计算(1)(a-b)2(a+b)2
;
(2)(x+y)(x-y)-(x+y)2.
=
(a2-b2)2
=
a4-2a2b2+b4
还有一种解法就是不用平方差公式,而是先分别用完全平方公式,再用多项式的乘法法则,但明显麻烦得多!
(2)(x+y)(x-y)-(x+y)2
=(x2-y2)-(x2+2xy+y2)
=
x2-y2-x2-2xy-y2
=
-2xy-2y2
(x+y)(x-y)-(x+y)2
(2)解法二:
=(x+y)[(x-y)-(x+y)]
=(x+y)(-2y)
例题示范
把一个正方形每边减少1cm所得的
新正方形的面积,恰好与原正方形相邻两边分别增加3cm和减少3cm后所得的长方形的面积相等,求原正方形的边长.
解:设原正方形的边长为xcm,
由题意得
答:原正方形的边长为5cm.
(x-1)2=(x+3)(x-3)
即
x2-2x+1=x2-9
解得
x=5
例题示范
1、计算:
(1)(a-2b)2(a+2b)2
(2)2(a+1)2-4(a+2)(a-2)+3(a-1)2
(3)20172-2016×2018
2、一个正方形的边长为acm,若边长增加6cm,则新正方形的面积增加多少?
3、已知x+y=2,xy=a+4,x2+y2=6,求a的值.
4、若a2+b2-6a-8b+25=0,求3a+4b的值.
5、已知x2+xy=14,y2+xy=2(x>y>0),
求值:(1)(x+y)2-x2+y2;(2)x+y;(3)x-y.
课后作业
3.2两数和(差)的平方1
公式的结构特征:
左边是
a2
?
b2
两个二项式的乘积,
(a+b)(a?b)=
即两数和与这两数差的积.
右边是
相同项平方与相反项平方之差,
即这两数的平方差.
温故知新
平方差公式
(a+b)2与(a+2b)2等于多少,而且要用拼图来说明。我到现在还没有结果呢,唉!今天上课又要挨批评了,
怎么办呢?同学们,你们能帮帮我吗?
昨天,数学老师布置了这样一道题目:
情境问题
(a+b)2=?
a
a
b
b
a2
ab
ab
b2
边长(a+b)的正方形,面积是(a+b)2.
将正方形分成四个部分,面积之和为a2+2ab+b2.
故:(a+b)2=a2+2ab+b2
探索发现
(a+2b)2=?
a2
ab
ab
b2
边长(a+2b)的正方形,面积是(a+2b)2.
将正方形分成9个部分,面积之和为a2+4ab+4b2.
故:(a+2b)2=a2+4ab+4b2
b
a
a
b
b
b
ab
ab
b2
b2
b2
探索发现
(a+2b)2=?
a2
还可以将边长为(a+2b)的正方形这样组合:
同样有(a+2b)2=a2+4ab+4b2
ab
a
a
b
b
b
b
ab
ab
ab
b2
b2
b2
b2
探索发现
认真观察这两个等式,你能发现什么规律吗?相互交流一下!
(a+b)2
=
a2+2ab+b2
(a+2b)2
=
a2+4ab+4b2
(a+3b)2
=
(3a+b)2
=
(2a+3b)2
=
牛
刀
小
试
a2+6ab+9b2
9a2+6ab+b2
4a2+12ab+9b2
用字母表示为:
这个公式叫两数和的平方公式.
两数和的平方,等于这两数的平方和加上它们积的2倍.
(a+b)2
=
a2+2ab+b2
等式左边是两个数(字母)和的平方.
等式右边可记为:
你平方、我平方、
你我2倍在中央.
(△+□)2
=
△2+2△□+□2
可形象地记为:
认真
观察
理解
抓住
关键
归纳
计算:
(1)(2a+3b)2;
(2)
(2a)2+2×2a?3b+(3b)2
(2)原式=
解:(1)原式=
=
4a2+12ab+9b2
对照公式:(△+□)2
=
△2+2△□+□2
准确找到公式中的△、□.
例题示范
根据两数和的平方公式,你能推导两数差的平方公式吗?
(a-b)2=?
解:
(a-b)2=[a+(-b)]2
将(a-b)理解成省略加号的代数和的形式.
=a2+2?a?(-b)+(-b)2
根据两数和的平方公式
=a2-2ab+b2
探索发现
这个公式叫两数差的平方公式.
两数差的平方,等于这两数的平方和减去它们积的2倍.
(a-b)2
=
a2-2ab+b2
(△-□)2
=
△2-2△□+□2
可形象地记为:
(a+b)2
=
a2+2ab+b2
(a-b)2
=
a2-2ab+b2
我俩有啥不同呢?
归纳
计算:
(1)(2a-3b)2;
(2)
(2a)2-2×2a?3b+(3b)2
(2)原式=
解:(1)原式=
=
4a2-12ab+9b2
对照公式:(△-□)2
=
△2-2△□+□2
准确找到公式中的△、□.
例题示范
(1)根据两数和(差)的平方公式填空:
(-a+b)2=
;
(-a-b)2=
;
(b-a)2
=
;
(b+a)2
=
.
a2-2ab+b2
a2+2ab+b2
b2-2ab+a2
b2+2ab+a2
认真观察,看看你能找到什么规律?相互交流一下
探索发现
(2)根据上述结果可归纳:
当二项式各项的符号相同时,
就用“和”的完全平方式;
当二项式各项的符号不同时,
就用“差”的完全平方式。
(a+b)2
=(-a-b)2=
a2+2ab+b2;
(a-b)2
=(-a+b)2=
a2-2ab+b2
1、两数和(差)的完全平方公式:
2、注意问题:
①必须符合完全平方公式特征的代数式才能用完全平方和(差)公式;
②完全平方和(差)公式可以逆用.
可理解为:两数和(差)的平方,等于这两数的平方和加上(减去)它们积的2倍.
(a+b)2
=(-a-b)2=
a2+2ab+b2;
(a-b)2
=(-a+b)2=
a2-2ab+b2
知识小结
P35练习1—3题;
P37习题12.3第2、3、4题.
课后阅读
P35“读一读”;P37“阅读材料”
课后作业
3.2两数和(差)的平方2
平方差公式:(a+b)(a-b)=
a2-b2
完全平方和(差)公式:
(a+b)2
=(-a-b)2=
a2+2ab+b2;
(a-b)2
=(-a+b)2=
a2-2ab+b2
注意:
必须符合公式特征的代数式才能用公式;
公式可以逆用.
回顾公式
1、下列等式中,不成立的是(
)
A.(3a-b)2=9a2-6ab+b2
B.(a+b-c)2=(c-a-b)2
C.(0.5x-y)2=0.25x2-xy+y2
D.(x+y)(x-y)(x2-y2)=x4-y4
2、判断下列计算是否正确:
(1).(-a2-b)2=a4-2a2b+b4
(
)
(2).(a-c)2=-(c-a)2
(
)
(3).(x3+2y)(x3-2y)=x9-4y2
(
)
(4).(5x-2y)(2y-5x)=-(5x-2y)2
(
)
×
×
×
√
D
练习巩固
4、若(x-y)2=0,则下列等式成立的是(
)
A.
x2+y2=2xy
B.
x2+y2=-2xy
C.
x2+y2=0
D.
x2-y2=0
C
3、下列多项式不能写成一个二项式
的平方的是(
)
A.9a2-6ab+b2
B.4t2+12t+9
C.
x2-4xy-4y2
D.
+m+m2
1
4
A
5、要得到(a-b)2,则a2+3ab+b2应加上(
)
A.
-ab
B.
-3ab
C.
-5ab
D.
-7ab
C
练习巩固
1、完全平方展开式:
例1:(1)如果x2
+ax+121是两个数的
和的平方形式,那么a的值是(
)
A.22
B.11
C.
±22
D.
±11
(x±11)2
=
x2±22x+121
C
(2)如果x2
+6x+k2
恰好是另一个整式的
平方,那么常数k的值是(
)
A.9
B.3
C.
-3
D.
±3
D
(3)如果x2+ax=(x+0.5)2+b,则(
)
A.a=1,b=0.25
B.a=1,b=-0.25
C.a=2,b=0.5
D.a=0,b=-0.5
x2+ax=x2+x+0.25+b
B
例题示范
1、完全平方展开式:
例2:无论x、y取何值时,代数式
x2
+y2
-2x+12y+38的值都是(
)
A.正数
B.负数
C.
零
D.
非负数
x2
+y2
-2x+12y+38
A
=(x2-2x+1)+(y2+12y+36)+1
=(x-1)2+(y+6)2+1
解:
∵(x-1)2≥0,(y+6)2≥0
∴无论x、y取何值,...的值都是正数.
例题示范
2.如何利用完全平方公式简便计算?
例:计算(1)1022
(2)99.82
(3)
解:
(1)原式=
(100+2)2
=
1002+2×100×2+22
=
10000+400+4
=
10404
如果是(-102)2呢?
(2)原式=
(100-0.2)2
=
1002-2×100×0.2+0.22
=
10000-40+0.04
=
9960.04
例题示范
(3)
解:
(3)原式=
如果是
呢?
关键是对底数进行变形:
例题示范
3、完全平方和与完全平方差的转换:
解析:
∵(a+b)2
=
a2+2ab+b2,
(a-b)2
=
a2-2ab+b2
例:填空(1)(a+b)2
=(a-b)2
+
;
(2)(a-b)2=(a+b)2
+
.
∴(a+b)2
+(a-b)2=
2a2+2b2,
(a+b)2
-(a-b)2=
4ab.
4ab
(-4ab)
根据上面的变形,我们能否这样做:
如果已知代数式a+b、a-b、ab、a2+b2中任意两个的值,就可以求出其余的值?
例题示范
1、已知(a+b)2=9,(a-b)2=5,则ab
=
;
练一练:
1
2、已知a+b=-2,ab
=1,则a2+b2=
;
(a+b)2
-(a-b)2=
4ab
(a+b)2=a2+b2+2ab
2
3、已知a+b=1,ab
=-1,则3a2+3b2=
;
a2+b2=(a+b)2-2ab
9
4、已知x+
=6,则x2+
=
;
34
5、已知a-
=2,则a2+
=
.
6
如图,从一块直径为a+b的圆形钢板中,挖去直径分别为a与b的两个圆,求出剩下钢板的面积.
解:由题意得
应用:
答:剩下钢板的面积为0.5πab.
4、完全平方与平方差的综合:
解:
(1)(a-b)2(a+b)2
=
[(a-b)(a+b)]2
例:计算(1)(a-b)2(a+b)2
;
(2)(x+y)(x-y)-(x+y)2.
=
(a2-b2)2
=
a4-2a2b2+b4
还有一种解法就是不用平方差公式,而是先分别用完全平方公式,再用多项式的乘法法则,但明显麻烦得多!
(2)(x+y)(x-y)-(x+y)2
=(x2-y2)-(x2+2xy+y2)
=
x2-y2-x2-2xy-y2
=
-2xy-2y2
(x+y)(x-y)-(x+y)2
(2)解法二:
=(x+y)[(x-y)-(x+y)]
=(x+y)(-2y)
例题示范
把一个正方形每边减少1cm所得的
新正方形的面积,恰好与原正方形相邻两边分别增加3cm和减少3cm后所得的长方形的面积相等,求原正方形的边长.
解:设原正方形的边长为xcm,
由题意得
答:原正方形的边长为5cm.
(x-1)2=(x+3)(x-3)
即
x2-2x+1=x2-9
解得
x=5
例题示范
1、计算:
(1)(a-2b)2(a+2b)2
(2)2(a+1)2-4(a+2)(a-2)+3(a-1)2
(3)20172-2016×2018
2、一个正方形的边长为acm,若边长增加6cm,则新正方形的面积增加多少?
3、已知x+y=2,xy=a+4,x2+y2=6,求a的值.
4、若a2+b2-6a-8b+25=0,求3a+4b的值.
5、已知x2+xy=14,y2+xy=2(x>y>0),
求值:(1)(x+y)2-x2+y2;(2)x+y;(3)x-y.
课后作业
