人教版八年级数学上册 13.1.1轴对称 课后练习(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册 13.1.1轴对称 课后练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 163.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 11:54:57 | ||
图片预览

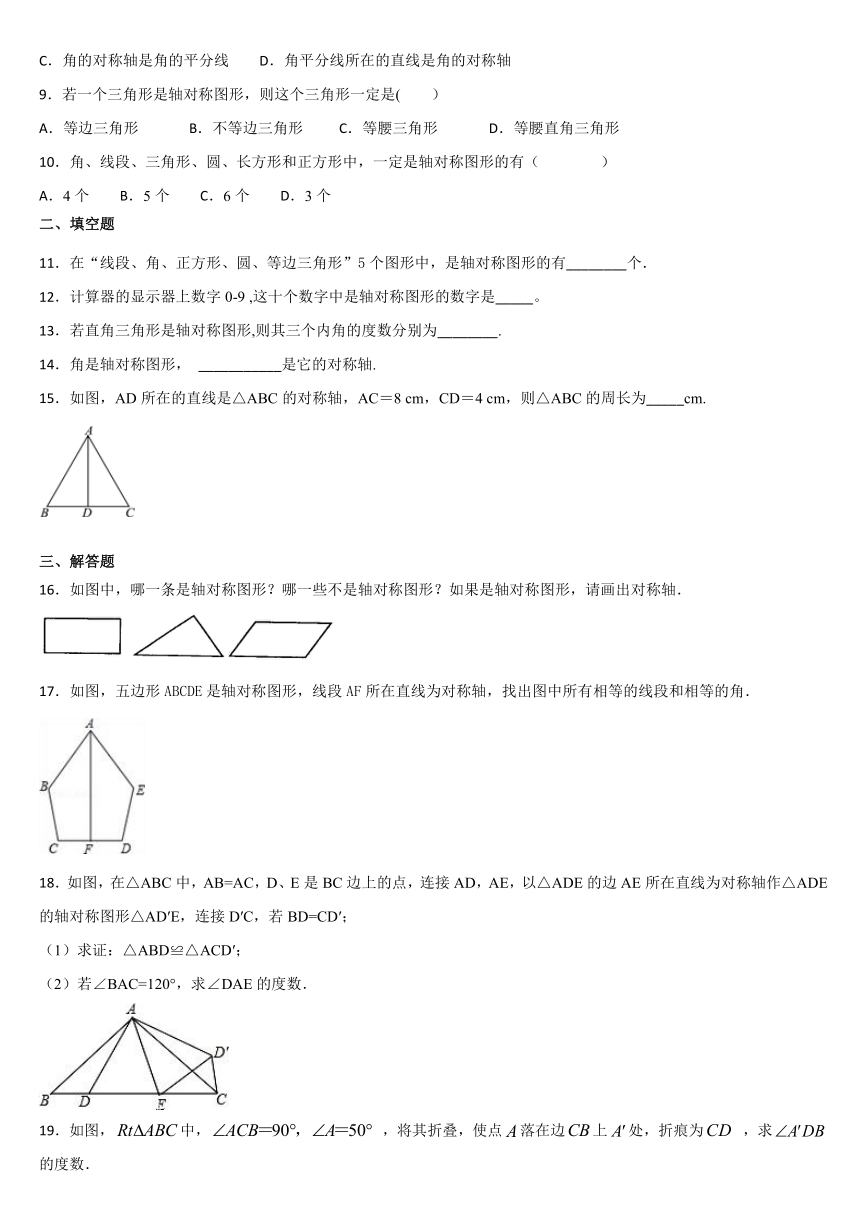
文档简介
人教版八年级数学上册
第十三章轴对称
13.1.1轴对称
课后练习
一、单选题
1.下列图形中,不是轴对称图形的是(
)
A.线段MN
B.两相交直线
C.射线
D.等边三角形
2.下列图形中轴对称图形的个数是(
).
?
A.1个
B.2个
C.3个
D.4个
3.下列图形中,不是轴对称图形的是(
)
A.有两个角相等的三角形;
B.有一个角为45°的直角三角形;
C.有一个内角为30°,一个内角为120°的三角形;
D.有一个内角为30°的直角三角形;
4.一个平面图形,如果沿着一条直线对折能做到自身重合,便称为轴对称图形,例如正方形是轴对称图形(因为沿它的一条对角线对折,可做到自身重合).在下图中的4个图形中有多少个是轴对称图形(
).
A.4
B.3
C.2
D.l
5.下列图形中,不是轴对称图形的是(
)
A.线段
B.等腰直角三角形
C.等边三角形
D.直角三角形
6.如图,正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′,下列判断错误的是(
)
A.AB=A′B′
B.BC∥B′C′
C.直线l⊥BB′
D.∠A′=120°
7.下列选项中的图形均为正多边形,其中恰有4条对称轴的是(
)
A.
B.
C.
D.
8.下列说法正确的是(
)
A.长方形有且只有一条对称轴
B.垂直于线段的直线就是线段的对称轴
C.角的对称轴是角的平分线
D.角平分线所在的直线是角的对称轴
9.若一个三角形是轴对称图形,则这个三角形一定是(
)
A.等边三角形
B.不等边三角形
C.等腰三角形
D.等腰直角三角形
10.角、线段、三角形、圆、长方形和正方形中,一定是轴对称图形的有(
)
A.4个
B.5个
C.6个
D.3个
二、填空题
11.在“线段、角、正方形、圆、等边三角形”5个图形中,是轴对称图形的有________个.
12.计算器的显示器上数字0-9
,这十个数字中是轴对称图形的数字是_____。
13.若直角三角形是轴对称图形,则其三个内角的度数分别为________.
14.角是轴对称图形,
___________是它的对称轴.
15.如图,AD所在的直线是△ABC的对称轴,AC=8
cm,CD=4
cm,则△ABC的周长为_____cm.
三、解答题
16.如图中,哪一条是轴对称图形?哪一些不是轴对称图形?如果是轴对称图形,请画出对称轴.
17.如图,五边形ABCDE是轴对称图形,线段AF所在直线为对称轴,找出图中所有相等的线段和相等的角.
18.如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.
19.如图,中,
,将其折叠,使点落在边上处,折痕为
,求
的度数.
20.有一些整数你无论从左往右看,还是从右往左看,数字都是完全一样,例如:22,131,1991,123321,…,像这样的数,我们称为“回文数”.回文数实际上是由左右排列对称的自然数构成的,有趣的是,当你遇到一个普通的数(两位以上),经过一定的计算,可以变成“回文数”.办法很简单:只要将这个数加上它的逆序数就可以了,若一次不成功,反复进行下去,一定能得到一个回文数,比如:①132+231=363;②7299+9927=17226,17226+62271=79497.
(1)你能用上述方法,将下列各数“变”成回文数吗?
①237;
②362.
(2)请写出一个四位数,并用上述方法将它变成回文数.
21.找出图中哪些是轴对称图形?并画出其对称轴.
22.国旗是一个国家的象征,你知道哪些国家的国旗?其中哪些国旗是轴对称图形?请你查阅相关的资料,尽可能多地找出是轴对称图形的国旗.
23.试画出下列正多边形的所有对称轴,并完成表格:
正多边形的边数
3
4
5
6
7
…
对称轴的条数
…
根据上表,猜想正n边形有________条对称轴.
【参考答案】
C
2.D
3.D
4.B
5.D
6.B
7.B
8.D
9.C
10.B
11.5
12.0,3,8
13.90°,45°,45°
14.角平分线所在的直线.
15.24
16.长方形是轴对称图形,其余不是
17.相等的线段:AB=AE,CB=DE,CF=DF;
相等的角:∠B=∠E,∠C=∠D,∠BAF=∠EAF,∠AFD=∠AFC.
18.()证明:∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
在△ABD和△ACD′中,
∵
,
∴
△ABD≌△ACD′(SSS).
()解:∵≌,
∴,
∴,
∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
即.
19.
20.(1)①969;②625;(2)2662
21.四幅图均为轴对称图形,其对称轴如下图:
22.略
23.解:如图.
故表格中依次填3,4,5,6,7;
猜想正n边形有n条对称轴.
第十三章轴对称
13.1.1轴对称
课后练习
一、单选题
1.下列图形中,不是轴对称图形的是(
)
A.线段MN
B.两相交直线
C.射线
D.等边三角形
2.下列图形中轴对称图形的个数是(
).
?
A.1个
B.2个
C.3个
D.4个
3.下列图形中,不是轴对称图形的是(
)
A.有两个角相等的三角形;
B.有一个角为45°的直角三角形;
C.有一个内角为30°,一个内角为120°的三角形;
D.有一个内角为30°的直角三角形;
4.一个平面图形,如果沿着一条直线对折能做到自身重合,便称为轴对称图形,例如正方形是轴对称图形(因为沿它的一条对角线对折,可做到自身重合).在下图中的4个图形中有多少个是轴对称图形(
).
A.4
B.3
C.2
D.l
5.下列图形中,不是轴对称图形的是(
)
A.线段
B.等腰直角三角形
C.等边三角形
D.直角三角形
6.如图,正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′,下列判断错误的是(
)
A.AB=A′B′
B.BC∥B′C′
C.直线l⊥BB′
D.∠A′=120°
7.下列选项中的图形均为正多边形,其中恰有4条对称轴的是(
)
A.
B.
C.
D.
8.下列说法正确的是(
)
A.长方形有且只有一条对称轴
B.垂直于线段的直线就是线段的对称轴
C.角的对称轴是角的平分线
D.角平分线所在的直线是角的对称轴
9.若一个三角形是轴对称图形,则这个三角形一定是(
)
A.等边三角形
B.不等边三角形
C.等腰三角形
D.等腰直角三角形
10.角、线段、三角形、圆、长方形和正方形中,一定是轴对称图形的有(
)
A.4个
B.5个
C.6个
D.3个
二、填空题
11.在“线段、角、正方形、圆、等边三角形”5个图形中,是轴对称图形的有________个.
12.计算器的显示器上数字0-9
,这十个数字中是轴对称图形的数字是_____。
13.若直角三角形是轴对称图形,则其三个内角的度数分别为________.
14.角是轴对称图形,
___________是它的对称轴.
15.如图,AD所在的直线是△ABC的对称轴,AC=8
cm,CD=4
cm,则△ABC的周长为_____cm.
三、解答题
16.如图中,哪一条是轴对称图形?哪一些不是轴对称图形?如果是轴对称图形,请画出对称轴.
17.如图,五边形ABCDE是轴对称图形,线段AF所在直线为对称轴,找出图中所有相等的线段和相等的角.
18.如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.
19.如图,中,
,将其折叠,使点落在边上处,折痕为
,求
的度数.
20.有一些整数你无论从左往右看,还是从右往左看,数字都是完全一样,例如:22,131,1991,123321,…,像这样的数,我们称为“回文数”.回文数实际上是由左右排列对称的自然数构成的,有趣的是,当你遇到一个普通的数(两位以上),经过一定的计算,可以变成“回文数”.办法很简单:只要将这个数加上它的逆序数就可以了,若一次不成功,反复进行下去,一定能得到一个回文数,比如:①132+231=363;②7299+9927=17226,17226+62271=79497.
(1)你能用上述方法,将下列各数“变”成回文数吗?
①237;
②362.
(2)请写出一个四位数,并用上述方法将它变成回文数.
21.找出图中哪些是轴对称图形?并画出其对称轴.
22.国旗是一个国家的象征,你知道哪些国家的国旗?其中哪些国旗是轴对称图形?请你查阅相关的资料,尽可能多地找出是轴对称图形的国旗.
23.试画出下列正多边形的所有对称轴,并完成表格:
正多边形的边数
3
4
5
6
7
…
对称轴的条数
…
根据上表,猜想正n边形有________条对称轴.
【参考答案】
C
2.D
3.D
4.B
5.D
6.B
7.B
8.D
9.C
10.B
11.5
12.0,3,8
13.90°,45°,45°
14.角平分线所在的直线.
15.24
16.长方形是轴对称图形,其余不是
17.相等的线段:AB=AE,CB=DE,CF=DF;
相等的角:∠B=∠E,∠C=∠D,∠BAF=∠EAF,∠AFD=∠AFC.
18.()证明:∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
在△ABD和△ACD′中,
∵
,
∴
△ABD≌△ACD′(SSS).
()解:∵≌,
∴,
∴,
∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
即.
19.
20.(1)①969;②625;(2)2662
21.四幅图均为轴对称图形,其对称轴如下图:
22.略
23.解:如图.
故表格中依次填3,4,5,6,7;
猜想正n边形有n条对称轴.
