人教版数学七年级上册 1.2.4 绝对值课件(共22张PPT)
文档属性
| 名称 | 人教版数学七年级上册 1.2.4 绝对值课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 757.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
预习:书本15、16、17页,完成下列问题
1.什么叫绝对值?.
2绝对值的性质是什么?.
3.绝对值与相反数的关系是什么?
4.绝对值的结果可能是负数吗?
6.完成作业本(2)中2、3两页
5.完成书中17页作业题1、2、3、4、5、6
7.完成步步高
第4、5两页
_____.
8.默写有理数分类表、数轴定义、相反数定义,
明天上课前要默写
规定了原点、单位长度、正方向的直线叫做数轴。
只有符号不同的两个数称为互为相反数。
a
a
相反数
规定:0的相反数是0。
在数轴上,表示互为相反数的两个点,位于原点
的两侧,并且与原点的距离相等。
相反数的几何意义:
什么叫数轴?
什么叫相反数?
怎样表示a的相反数?
(1)甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正。两辆出租车都从O地出发,甲车向东行驶6km到达A处,记做_____km,乙车向西行驶6km到达B处,记做_____km.
以O为原点,取适当的单位长度画数轴,并在数轴上标出点A,B的位置,则A,B两点到原点的距离分别是多少?它们的实际意义是什么?
+6
-6
A、B两点到原点的距离都是6个单位长,它们的实际意义是不考虑方向时,两车行驶的里程都是6km.
2、数轴上表示-5与5的点到原点的距离分别是多少?
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
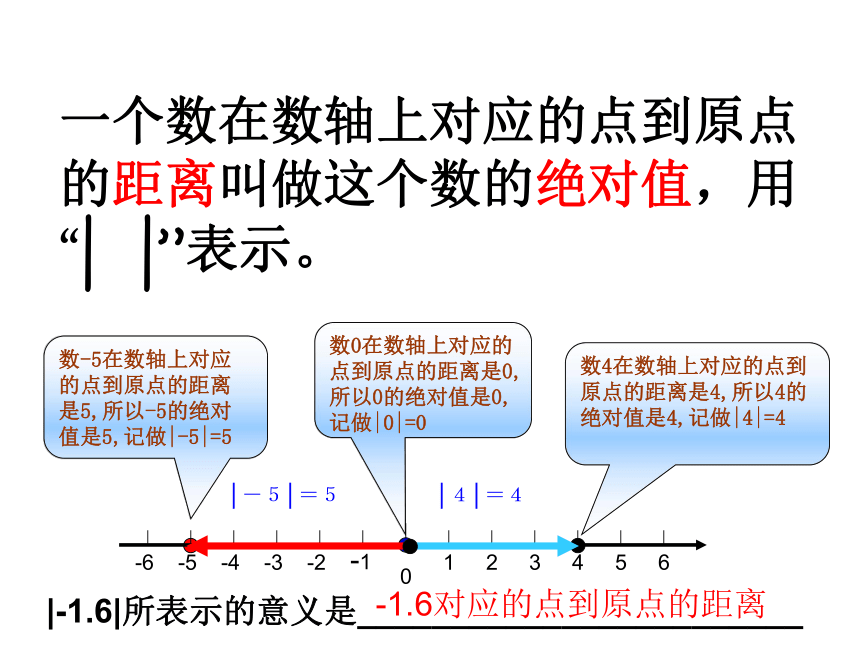
数4在数轴上对应的点到原点的距离是4,所以4的绝对值是4,记做|4|=4
数-5在数轴上对应的点到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“|
|”表示。
数0在数轴上对应的点到原点的距离是0,所以0的绝对值是0,记做|0|=0
|-1.6|所表示的意义是________________________
-1.6对应的点到原点的距离
解:
|-1.6|
1.6
|0|
0
|-10|
10
=
=
=
=
例1
求下列各数的绝对值:
-1.6,+
,0,-10,
10
8
5
|+
|
8
5
8
5
|10|
10
=
一个正数的绝对值是它本身
一个负数的绝对值是它的相反数
零的绝对值是零
议一议:一个数的绝对值与这个数有什么关系?
任何有理数的绝对值都是非负数。
求下列各组数的绝对值:
(1)5,-5;
(2)
0.8,-0.8;(3)
想一想
互为相反数的两个数的绝对值有什么关系?
解:
(1)|5|=5
|-5|=5
(2)|0.8|=0.8
|-0.8|=0.8
相等
|
|=
|-
|=
(3)
口答:说出下列各数的绝对值。
-7,0,-2.05,1000,
7/9
绝对值的性质:
一个正数的绝对值是它本身
一个负数的绝对值是它的相反数
零的绝对值是零
互为相反数的两个数的绝对值相等
注意:任何有理数的绝对值都是非负数。
变变:计算:
(1)
|-9|+|+1|
(2)
|-10|-|-8|
(3)
|-3|×|6.2|
例2
求绝对值等于4的数。
解:
∵数轴上到原点的距离等于4个单位长度的点有两个,即表示+4的点P和-4的点M,
∴绝对值等于4的数是+4和-4.
0
1
2
3
4
5
-1
-2
-3
-4
-5
4
4
P
M
(1)一个数的绝对值一定是正数。
(
)
(2)一个数的绝对值不可能是负数。
(
)
(3)绝对值是同一个正数的数有两个,且
它们是互为相反数。
(
)
×,是正数或零
√
√
3.下面的说法对吗?如果不对,应如何改正?
(1)一个数的绝对值是它本身,这个数是(
).
正数或零
(2)一个数的绝对值是它的相反数,这个数是(
).
负数或零
如果
|
a
|
=
a
,
a
?
0
.
如果
|
a
|
=
-a
,
a
?
0
.
(3)一个数的相反数是它本身,这个数是(
).
零
正数的绝对值是它本身
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3)当a=0时,|a|=___。
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
|a|≧0
试一试:
若字母a表示一个有理数,你知道a的绝对值等于什么吗?
-1或-5
它的实际意义是出租车行驶的总里程是24km.
±4
2
-6
7.2
2
1
、|2|=______,|-2|=______
2、若|x|=4,则x=______,
3、若|a|=0,则a=______
4、|-6|的相反数是______
5、+7.2的相反数的绝对值是______
一、填空:
0
│x│=│-3│,x=______,
±3
6、绝对值小于
4
的整数有(
)个。
7、绝对值不大于
5的负整数是
(
)
7
-1,-2,-3,-4,-5
8、绝对值大于
而小于
的整数是
(
)。
2
3
8
3
+1,-1,+2,-2
答:第五个排球的质量好一些,因为它的绝对值最小,
也就是离标准质量的克数最近。
正式排球比赛对所用的排球重量是有严格规定的,现检查5个排球的重量,超过规定重量的克数记作正数,不足规定重量的克数记作负数,检查结果如下:
问题:
指出哪个排球的质量好一些,并用绝对值的知识加以说明。
应用:
2.电子跳蚤落在数轴上的某点k0,第一步从k0向左跳1个单位到k1,第二步由k1向右跳2个单位到k2,第三步由k2向左跳3个单位到k3,第四步由k3向右跳4个单位到k4,…,按以上规律跳了100步时,电子跳蚤落在数轴上的点k100所表示的数恰是30.则电子跳蚤的初始位置k0点所表示的数是_____.
探究:
1、若|a|+|b-1|=0,则a=_____,
b=_____.
0
1
-20
1.有理数的绝对值的意义.
该有理数到原点的距离
2.绝对值的性质:一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
零的绝对值是零;
互为相反数的两个数的绝对值相等
理一理
3.绝对值的非负性:
4.绝对值与相反数的关系:
|a|≥0(非负性)
互为相反数的两个数的绝对值相等;
绝对值相等,符号相反的两个数互为相反数;
若|a|=|b|,则a=b或者a=-b
5.绝对值等于本身的数:
6.绝对值为非零数,则
0和正数(非负数)
原数有2个,且互为相反数
1、│a-2│+│b-3│+│c-4│=0,则a+2b+3c=
__________
。
4、已知│x+3│=0,
则x=
;
若│x+3│=2,
则x=
。
2、如果a,b互为相反数,c,d互为倒数,x的绝对值是1,
求代数式
的值
3、已知│a│=3,│b│=5,a与b异号,求│a-b│的值。
(1)
若一个数的绝对值是
2,则这个数是2。
(2)若a=b,则|a|=|b|。
(3)若|a|=|b|,则a=b。
(4)若|a|=-a,则a必为负数。
(5)绝对值相等,符号相反的两个数是互为相
反数。
×
√
×
×
√
二、判断题
预习:书本15、16、17页,完成下列问题
1.什么叫绝对值?.
2绝对值的性质是什么?.
3.绝对值与相反数的关系是什么?
4.绝对值的结果可能是负数吗?
6.完成作业本(2)中2、3两页
5.完成书中17页作业题1、2、3、4、5、6
7.完成步步高
第4、5两页
_____.
8.默写有理数分类表、数轴定义、相反数定义,
明天上课前要默写
规定了原点、单位长度、正方向的直线叫做数轴。
只有符号不同的两个数称为互为相反数。
a
a
相反数
规定:0的相反数是0。
在数轴上,表示互为相反数的两个点,位于原点
的两侧,并且与原点的距离相等。
相反数的几何意义:
什么叫数轴?
什么叫相反数?
怎样表示a的相反数?
(1)甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正。两辆出租车都从O地出发,甲车向东行驶6km到达A处,记做_____km,乙车向西行驶6km到达B处,记做_____km.
以O为原点,取适当的单位长度画数轴,并在数轴上标出点A,B的位置,则A,B两点到原点的距离分别是多少?它们的实际意义是什么?
+6
-6
A、B两点到原点的距离都是6个单位长,它们的实际意义是不考虑方向时,两车行驶的里程都是6km.
2、数轴上表示-5与5的点到原点的距离分别是多少?
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
数4在数轴上对应的点到原点的距离是4,所以4的绝对值是4,记做|4|=4
数-5在数轴上对应的点到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“|
|”表示。
数0在数轴上对应的点到原点的距离是0,所以0的绝对值是0,记做|0|=0
|-1.6|所表示的意义是________________________
-1.6对应的点到原点的距离
解:
|-1.6|
1.6
|0|
0
|-10|
10
=
=
=
=
例1
求下列各数的绝对值:
-1.6,+
,0,-10,
10
8
5
|+
|
8
5
8
5
|10|
10
=
一个正数的绝对值是它本身
一个负数的绝对值是它的相反数
零的绝对值是零
议一议:一个数的绝对值与这个数有什么关系?
任何有理数的绝对值都是非负数。
求下列各组数的绝对值:
(1)5,-5;
(2)
0.8,-0.8;(3)
想一想
互为相反数的两个数的绝对值有什么关系?
解:
(1)|5|=5
|-5|=5
(2)|0.8|=0.8
|-0.8|=0.8
相等
|
|=
|-
|=
(3)
口答:说出下列各数的绝对值。
-7,0,-2.05,1000,
7/9
绝对值的性质:
一个正数的绝对值是它本身
一个负数的绝对值是它的相反数
零的绝对值是零
互为相反数的两个数的绝对值相等
注意:任何有理数的绝对值都是非负数。
变变:计算:
(1)
|-9|+|+1|
(2)
|-10|-|-8|
(3)
|-3|×|6.2|
例2
求绝对值等于4的数。
解:
∵数轴上到原点的距离等于4个单位长度的点有两个,即表示+4的点P和-4的点M,
∴绝对值等于4的数是+4和-4.
0
1
2
3
4
5
-1
-2
-3
-4
-5
4
4
P
M
(1)一个数的绝对值一定是正数。
(
)
(2)一个数的绝对值不可能是负数。
(
)
(3)绝对值是同一个正数的数有两个,且
它们是互为相反数。
(
)
×,是正数或零
√
√
3.下面的说法对吗?如果不对,应如何改正?
(1)一个数的绝对值是它本身,这个数是(
).
正数或零
(2)一个数的绝对值是它的相反数,这个数是(
).
负数或零
如果
|
a
|
=
a
,
a
?
0
.
如果
|
a
|
=
-a
,
a
?
0
.
(3)一个数的相反数是它本身,这个数是(
).
零
正数的绝对值是它本身
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3)当a=0时,|a|=___。
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
|a|≧0
试一试:
若字母a表示一个有理数,你知道a的绝对值等于什么吗?
-1或-5
它的实际意义是出租车行驶的总里程是24km.
±4
2
-6
7.2
2
1
、|2|=______,|-2|=______
2、若|x|=4,则x=______,
3、若|a|=0,则a=______
4、|-6|的相反数是______
5、+7.2的相反数的绝对值是______
一、填空:
0
│x│=│-3│,x=______,
±3
6、绝对值小于
4
的整数有(
)个。
7、绝对值不大于
5的负整数是
(
)
7
-1,-2,-3,-4,-5
8、绝对值大于
而小于
的整数是
(
)。
2
3
8
3
+1,-1,+2,-2
答:第五个排球的质量好一些,因为它的绝对值最小,
也就是离标准质量的克数最近。
正式排球比赛对所用的排球重量是有严格规定的,现检查5个排球的重量,超过规定重量的克数记作正数,不足规定重量的克数记作负数,检查结果如下:
问题:
指出哪个排球的质量好一些,并用绝对值的知识加以说明。
应用:
2.电子跳蚤落在数轴上的某点k0,第一步从k0向左跳1个单位到k1,第二步由k1向右跳2个单位到k2,第三步由k2向左跳3个单位到k3,第四步由k3向右跳4个单位到k4,…,按以上规律跳了100步时,电子跳蚤落在数轴上的点k100所表示的数恰是30.则电子跳蚤的初始位置k0点所表示的数是_____.
探究:
1、若|a|+|b-1|=0,则a=_____,
b=_____.
0
1
-20
1.有理数的绝对值的意义.
该有理数到原点的距离
2.绝对值的性质:一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
零的绝对值是零;
互为相反数的两个数的绝对值相等
理一理
3.绝对值的非负性:
4.绝对值与相反数的关系:
|a|≥0(非负性)
互为相反数的两个数的绝对值相等;
绝对值相等,符号相反的两个数互为相反数;
若|a|=|b|,则a=b或者a=-b
5.绝对值等于本身的数:
6.绝对值为非零数,则
0和正数(非负数)
原数有2个,且互为相反数
1、│a-2│+│b-3│+│c-4│=0,则a+2b+3c=
__________
。
4、已知│x+3│=0,
则x=
;
若│x+3│=2,
则x=
。
2、如果a,b互为相反数,c,d互为倒数,x的绝对值是1,
求代数式
的值
3、已知│a│=3,│b│=5,a与b异号,求│a-b│的值。
(1)
若一个数的绝对值是
2,则这个数是2。
(2)若a=b,则|a|=|b|。
(3)若|a|=|b|,则a=b。
(4)若|a|=-a,则a必为负数。
(5)绝对值相等,符号相反的两个数是互为相
反数。
×
√
×
×
√
二、判断题
