人教版九年级数学上册 24.1.2垂直于弦的直径练习 (word 版 含解析)
文档属性
| 名称 | 人教版九年级数学上册 24.1.2垂直于弦的直径练习 (word 版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 352.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 00:00:00 | ||
图片预览


文档简介
人教版九年级数学上册24.1.2垂直于弦的直径
一.选择题(共6小题)
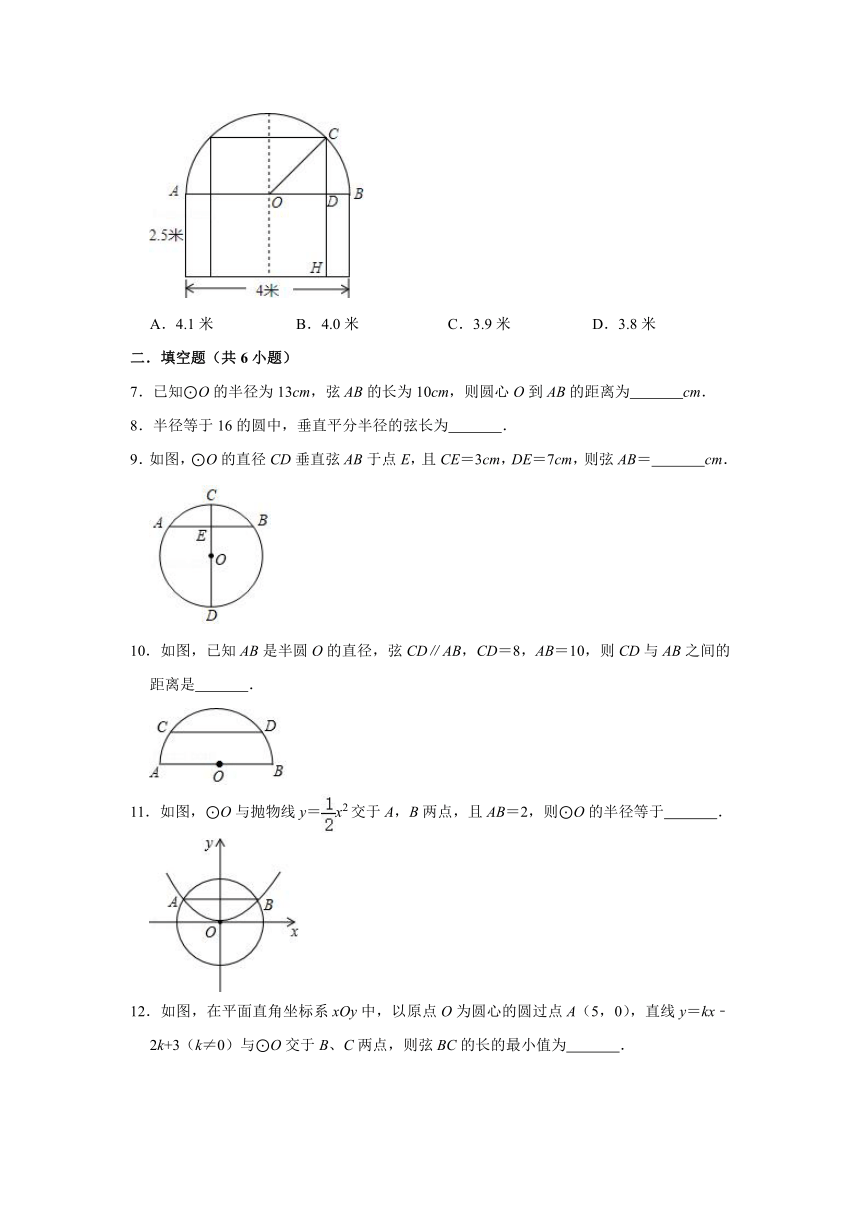
1.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于90°,那么圆心O到弦AB的距离为( )
A.
B.2
C.2
D.3
2.如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(0,3),则该圆弧所在圆的圆心坐标是( )
A.(0,0)
B.(1,1)
C.(0,1)
D.(1、0)
3.如图,⊙O中,OD⊥AB于点C,OB=13,AB=24,则OC的长为( )
A.3
B.4
C.5
D.6
4.在半径为50mm的⊙O中,弦AB的长为50mm,则点O到AB的距离为( )
A.50mm
B.25mm
C.25mm
D.25mm
5.AB和CD是⊙O的两条平行弦,AB=6,CD=8,⊙O的半径为5,则AB与CD间的距离为( )
A.1
B.7
C.1或7
D.3或4
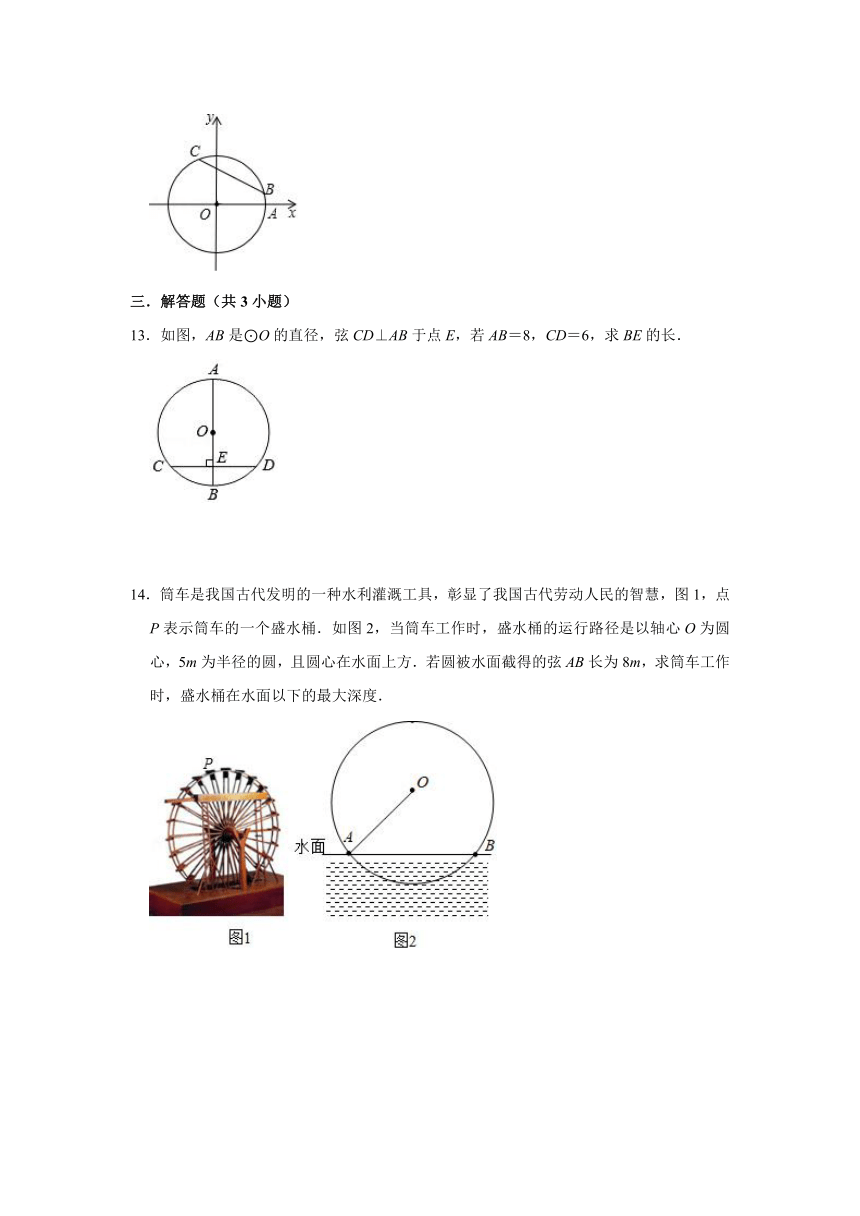
6.一辆装满货物,宽为2.4米的卡车,欲通过如图的隧道,则卡车的外形高必须低于( )
A.4.1米
B.4.0米
C.3.9米
D.3.8米
二.填空题(共6小题)
7.已知⊙O的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为
cm.
8.半径等于16的圆中,垂直平分半径的弦长为
.
9.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB=
cm.
10.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是
.
11.如图,⊙O与抛物线y=x2交于A,B两点,且AB=2,则⊙O的半径等于
.
12.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(5,0),直线y=kx﹣2k+3(k≠0)与⊙O交于B、C两点,则弦BC的长的最小值为
.
三.解答题(共3小题)
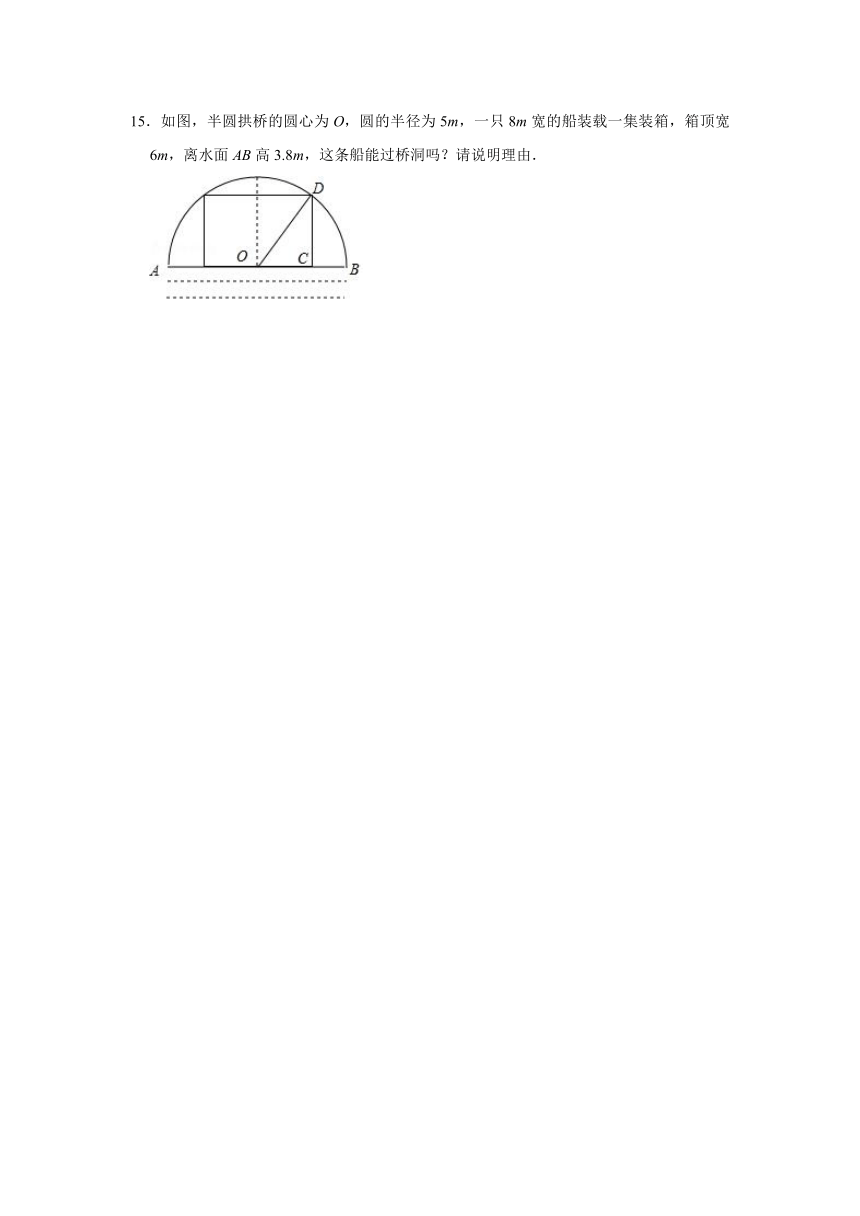
13.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,求BE的长.
14.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.
15.如图,半圆拱桥的圆心为O,圆的半径为5m,一只8m宽的船装载一集装箱,箱顶宽6m,离水面AB高3.8m,这条船能过桥洞吗?请说明理由.
人教版九年级数学上册24.1.2垂直于弦的直径参考答案
一.选择题(共6小题)
1.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于90°,那么圆心O到弦AB的距离为( )
A.
B.2
C.2
D.3
【解答】解:过O作OC⊥AB于C,
∵OA=OB=4,∠AOB=90°,
∴AB=OA=4,
∴OC=AB=2,
故选:C.
2.如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(0,3),则该圆弧所在圆的圆心坐标是( )
A.(0,0)
B.(1,1)
C.(0,1)
D.(1、0)
【解答】解:该圆弧所在圆的圆心坐标是:(1,0).
故选:D.
3.如图,⊙O中,OD⊥AB于点C,OB=13,AB=24,则OC的长为( )
A.3
B.4
C.5
D.6
【解答】解:∵OD⊥AB,
∴AC=BC=AB=×24=12,
在Rt△OBC中,OC==5.
故选:C.
4.在半径为50mm的⊙O中,弦AB的长为50mm,则点O到AB的距离为( )
A.50mm
B.25mm
C.25mm
D.25mm
【解答】解:作OC⊥AB于C,
根据题意:OA=OB=AB=50mm,
∴△AOB是等边三角形,
∴∠AOC=30°,
∴OC=OA?cos30°=25cm.
故选:B.
5.AB和CD是⊙O的两条平行弦,AB=6,CD=8,⊙O的半径为5,则AB与CD间的距离为( )
A.1
B.7
C.1或7
D.3或4
【解答】解:①当AB、CD在圆心两侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图所示:
∵半径r=5,弦AB∥CD,且AB=6,CD=8,
∴OA=OC=5,CE=DE=4,AF=FB=3,E、F、O在一条直线上,
∴EF为AB、CD之间的距离
在Rt△OEC中,由勾股定理可得:
OE2=OC2﹣CE2
∴OE==3,
在Rt△OFA中,由勾股定理可得:
OF2=OA2﹣AF2
∴OF==4,
∴EF=OE+OF=3+4=7,
AB与CD的距离为7;
②当AB、CD在圆心同侧时;
同①可得:OE=3,OF=4;
则AB与CD的距离为:OF﹣OE=1;
综上所述:AB与CD间的距离为1或7.
故选:C.
6.一辆装满货物,宽为2.4米的卡车,欲通过如图的隧道,则卡车的外形高必须低于( )
A.4.1米
B.4.0米
C.3.9米
D.3.8米
【解答】解:∵车宽2.4米,
∴欲通过如图的隧道,只要比较距隧道中线1.2米处的高度与车高.
在Rt△OCD中,由勾股定理可得:
CD===1.6(m),
CH=CD+DH=1.6+2.5=4.1米,
∴卡车的外形高必须低于4.1米.
故选:A.
二.填空题(共6小题)
7.已知⊙O的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为 12 cm.
【解答】解:如图,作OC⊥AB于C,连接OA,
则AC=BC=AB=5,
在Rt△OAC中,OC==12,
所以圆心O到AB的距离为12cm.
故答案为12.
8.半径等于16的圆中,垂直平分半径的弦长为 16 .
【解答】解:如图,OA=16,则OC=8,
根据勾股定理得,AC==8,
∴弦AB=16.
故答案为:16.
9.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB= 2 cm.
【解答】解:连接OA,如图,
∵CE=3,DE=7,
∴CD=10,
∴OC=OA=5,OE=2,
∵AB⊥CD,
∴AE=BE,
在Rt△AOE中,AE==,
∴AB=2AE=2(cm).
故答案为2.
10.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 3 .
【解答】解:过点O作OH⊥CD于H,连接OC,如图,则CH=DH=CD=4,
在Rt△OCH中,OH==3,
所以CD与AB之间的距离是3.
故答案为3.
11.如图,⊙O与抛物线y=x2交于A,B两点,且AB=2,则⊙O的半径等于 .
【解答】解:连接OA,设AB与y轴交于点C,
∵AB=2,
∴点A,B的横坐标分别为﹣1,1.
∵⊙O与抛物线y=x2交于A,B两点,
点A,B的坐标分别为(﹣1,),(1,),
在Rt△OAC中,由勾股定理得OA===,
∴⊙O的半径为.
12.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(5,0),直线y=kx﹣2k+3(k≠0)与⊙O交于B、C两点,则弦BC的长的最小值为 4 .
【解答】解:对于直线y=kx﹣2k+3=k(x﹣2)+3,当x=2时,y=3,
故直线y=kx﹣2k+3恒经过点(2,3),记为点D.
过点D作DH⊥x轴于点H,
则有OH=2,DH=3,OD==.
∵点A(5,0),
∴OA=5,
∴OB=OA=5.
由于过圆内定点D的所有弦中,与OD垂直的弦最短,如图所示,
因此运用垂径定理及勾股定理可得:
BC的最小值为2BD=2=2×=4.
故答案为4.
三.解答题(共3小题)
13.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,求BE的长.
【解答】解:如图,连接OC.
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=CD=3.
∵在Rt△OEC中,∠OEC=90°,CE=3,OC=4,
∴OE==,
∴BE=OB﹣OE=4﹣.
14.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.
【解答】解:过O点作半径OD⊥AB于E,如图,
∴AE=BE=AB=×8=4,
在Rt△AEO中,OE===3,
∴ED=OD﹣OE=5﹣3=2,
答:筒车工作时,盛水桶在水面以下的最大深度为2m.
15.如图,半圆拱桥的圆心为O,圆的半径为5m,一只8m宽的船装载一集装箱,箱顶宽6m,离水面AB高3.8m,这条船能过桥洞吗?请说明理由.
【解答】解:如图,过点O作OF⊥DE于点F,则EF=DF=DE,
假设DE=6m,则DF=3m,
∵圆的半径为5m,
∴OD=5m,
∴OF===4>3.8,
∴这条船能过桥洞.
一.选择题(共6小题)
1.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于90°,那么圆心O到弦AB的距离为( )
A.
B.2
C.2
D.3
2.如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(0,3),则该圆弧所在圆的圆心坐标是( )
A.(0,0)
B.(1,1)
C.(0,1)
D.(1、0)
3.如图,⊙O中,OD⊥AB于点C,OB=13,AB=24,则OC的长为( )
A.3
B.4
C.5
D.6
4.在半径为50mm的⊙O中,弦AB的长为50mm,则点O到AB的距离为( )
A.50mm
B.25mm
C.25mm
D.25mm
5.AB和CD是⊙O的两条平行弦,AB=6,CD=8,⊙O的半径为5,则AB与CD间的距离为( )
A.1
B.7
C.1或7
D.3或4
6.一辆装满货物,宽为2.4米的卡车,欲通过如图的隧道,则卡车的外形高必须低于( )
A.4.1米
B.4.0米
C.3.9米
D.3.8米
二.填空题(共6小题)
7.已知⊙O的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为
cm.
8.半径等于16的圆中,垂直平分半径的弦长为
.
9.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB=
cm.
10.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是
.
11.如图,⊙O与抛物线y=x2交于A,B两点,且AB=2,则⊙O的半径等于
.
12.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(5,0),直线y=kx﹣2k+3(k≠0)与⊙O交于B、C两点,则弦BC的长的最小值为
.
三.解答题(共3小题)
13.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,求BE的长.
14.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.
15.如图,半圆拱桥的圆心为O,圆的半径为5m,一只8m宽的船装载一集装箱,箱顶宽6m,离水面AB高3.8m,这条船能过桥洞吗?请说明理由.
人教版九年级数学上册24.1.2垂直于弦的直径参考答案
一.选择题(共6小题)
1.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于90°,那么圆心O到弦AB的距离为( )
A.
B.2
C.2
D.3
【解答】解:过O作OC⊥AB于C,
∵OA=OB=4,∠AOB=90°,
∴AB=OA=4,
∴OC=AB=2,
故选:C.
2.如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(0,3),则该圆弧所在圆的圆心坐标是( )
A.(0,0)
B.(1,1)
C.(0,1)
D.(1、0)
【解答】解:该圆弧所在圆的圆心坐标是:(1,0).
故选:D.
3.如图,⊙O中,OD⊥AB于点C,OB=13,AB=24,则OC的长为( )
A.3
B.4
C.5
D.6
【解答】解:∵OD⊥AB,
∴AC=BC=AB=×24=12,
在Rt△OBC中,OC==5.
故选:C.
4.在半径为50mm的⊙O中,弦AB的长为50mm,则点O到AB的距离为( )
A.50mm
B.25mm
C.25mm
D.25mm
【解答】解:作OC⊥AB于C,
根据题意:OA=OB=AB=50mm,
∴△AOB是等边三角形,
∴∠AOC=30°,
∴OC=OA?cos30°=25cm.
故选:B.
5.AB和CD是⊙O的两条平行弦,AB=6,CD=8,⊙O的半径为5,则AB与CD间的距离为( )
A.1
B.7
C.1或7
D.3或4
【解答】解:①当AB、CD在圆心两侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图所示:
∵半径r=5,弦AB∥CD,且AB=6,CD=8,
∴OA=OC=5,CE=DE=4,AF=FB=3,E、F、O在一条直线上,
∴EF为AB、CD之间的距离
在Rt△OEC中,由勾股定理可得:
OE2=OC2﹣CE2
∴OE==3,
在Rt△OFA中,由勾股定理可得:
OF2=OA2﹣AF2
∴OF==4,
∴EF=OE+OF=3+4=7,
AB与CD的距离为7;
②当AB、CD在圆心同侧时;
同①可得:OE=3,OF=4;
则AB与CD的距离为:OF﹣OE=1;
综上所述:AB与CD间的距离为1或7.
故选:C.
6.一辆装满货物,宽为2.4米的卡车,欲通过如图的隧道,则卡车的外形高必须低于( )
A.4.1米
B.4.0米
C.3.9米
D.3.8米
【解答】解:∵车宽2.4米,
∴欲通过如图的隧道,只要比较距隧道中线1.2米处的高度与车高.
在Rt△OCD中,由勾股定理可得:
CD===1.6(m),
CH=CD+DH=1.6+2.5=4.1米,
∴卡车的外形高必须低于4.1米.
故选:A.
二.填空题(共6小题)
7.已知⊙O的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为 12 cm.
【解答】解:如图,作OC⊥AB于C,连接OA,
则AC=BC=AB=5,
在Rt△OAC中,OC==12,
所以圆心O到AB的距离为12cm.
故答案为12.
8.半径等于16的圆中,垂直平分半径的弦长为 16 .
【解答】解:如图,OA=16,则OC=8,
根据勾股定理得,AC==8,
∴弦AB=16.
故答案为:16.
9.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB= 2 cm.
【解答】解:连接OA,如图,
∵CE=3,DE=7,
∴CD=10,
∴OC=OA=5,OE=2,
∵AB⊥CD,
∴AE=BE,
在Rt△AOE中,AE==,
∴AB=2AE=2(cm).
故答案为2.
10.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 3 .
【解答】解:过点O作OH⊥CD于H,连接OC,如图,则CH=DH=CD=4,
在Rt△OCH中,OH==3,
所以CD与AB之间的距离是3.
故答案为3.
11.如图,⊙O与抛物线y=x2交于A,B两点,且AB=2,则⊙O的半径等于 .
【解答】解:连接OA,设AB与y轴交于点C,
∵AB=2,
∴点A,B的横坐标分别为﹣1,1.
∵⊙O与抛物线y=x2交于A,B两点,
点A,B的坐标分别为(﹣1,),(1,),
在Rt△OAC中,由勾股定理得OA===,
∴⊙O的半径为.
12.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(5,0),直线y=kx﹣2k+3(k≠0)与⊙O交于B、C两点,则弦BC的长的最小值为 4 .
【解答】解:对于直线y=kx﹣2k+3=k(x﹣2)+3,当x=2时,y=3,
故直线y=kx﹣2k+3恒经过点(2,3),记为点D.
过点D作DH⊥x轴于点H,
则有OH=2,DH=3,OD==.
∵点A(5,0),
∴OA=5,
∴OB=OA=5.
由于过圆内定点D的所有弦中,与OD垂直的弦最短,如图所示,
因此运用垂径定理及勾股定理可得:
BC的最小值为2BD=2=2×=4.
故答案为4.
三.解答题(共3小题)
13.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,求BE的长.
【解答】解:如图,连接OC.
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=CD=3.
∵在Rt△OEC中,∠OEC=90°,CE=3,OC=4,
∴OE==,
∴BE=OB﹣OE=4﹣.
14.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.
【解答】解:过O点作半径OD⊥AB于E,如图,
∴AE=BE=AB=×8=4,
在Rt△AEO中,OE===3,
∴ED=OD﹣OE=5﹣3=2,
答:筒车工作时,盛水桶在水面以下的最大深度为2m.
15.如图,半圆拱桥的圆心为O,圆的半径为5m,一只8m宽的船装载一集装箱,箱顶宽6m,离水面AB高3.8m,这条船能过桥洞吗?请说明理由.
【解答】解:如图,过点O作OF⊥DE于点F,则EF=DF=DE,
假设DE=6m,则DF=3m,
∵圆的半径为5m,
∴OD=5m,
∴OF===4>3.8,
∴这条船能过桥洞.
同课章节目录
