六年级上册数学课件-圆的认识 35页PPT 北师大版
文档属性
| 名称 | 六年级上册数学课件-圆的认识 35页PPT 北师大版 |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 12:25:25 | ||
图片预览






文档简介
(共35张PPT)
圆的认识
温故知新:我们学过哪些几何平面图形?
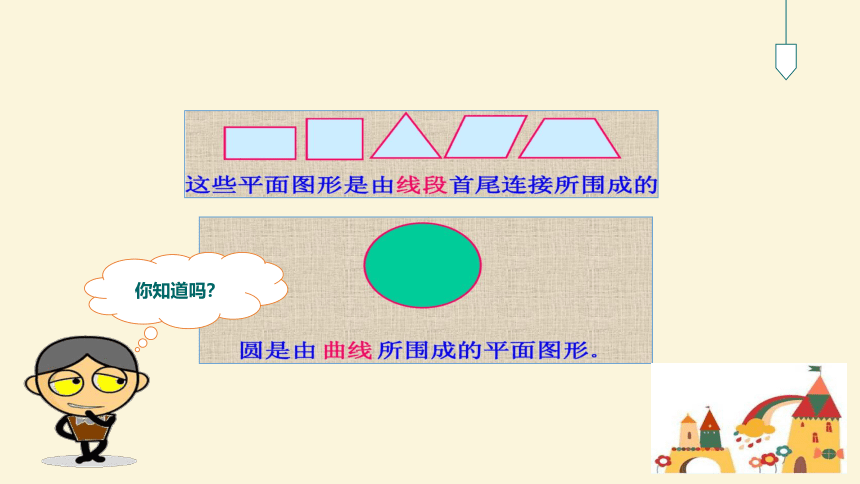
一起来“找茬”——哪里有圆形?
你知道吗?
一起来玩个游戏吧!
哪种方式更公平呢?
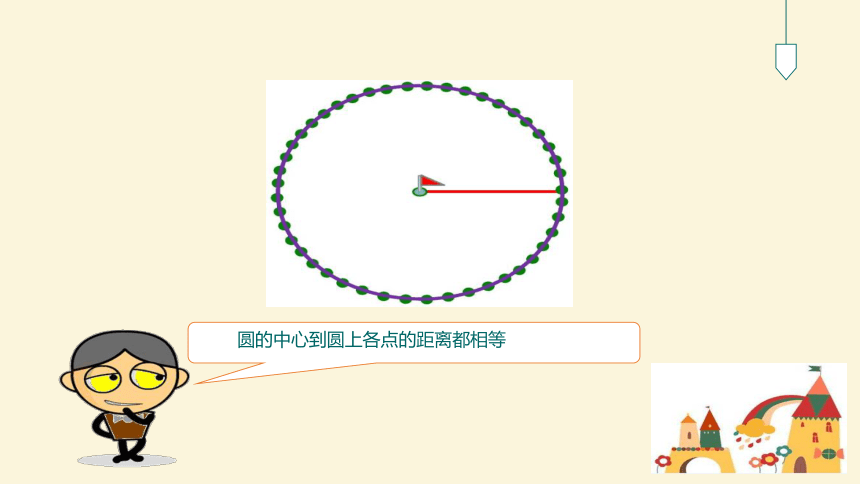
圆的中心到圆上各点的距离都相等
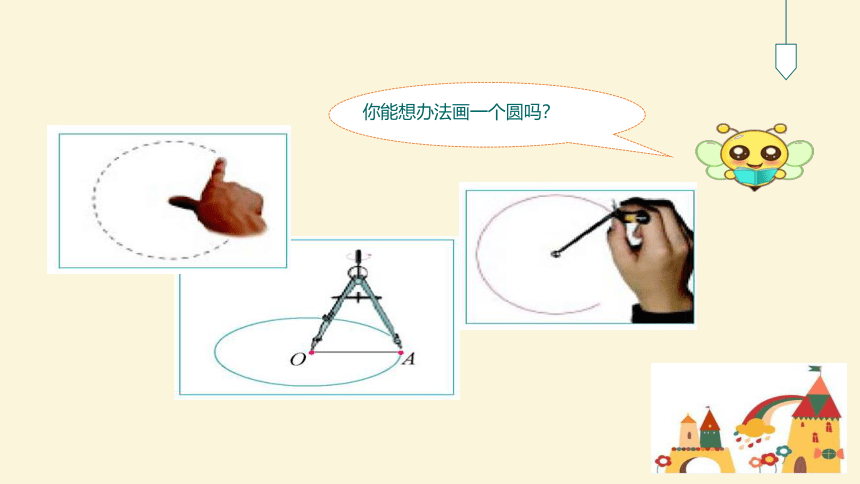
你能想办法画一个圆吗?
画一画,剪一剪。
用圆规画图
0
1
2
3
4
6
7
8
5
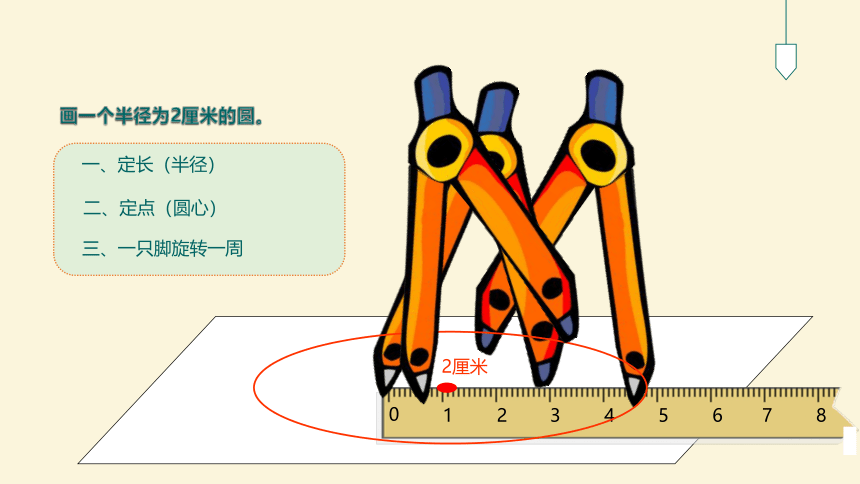
画一个半径为2厘米的圆。
一、定长(半径)
二、定点(圆心)
三、一只脚旋转一周
2厘米
折一折
折过若干次后,可以发现什么?
圆心
o
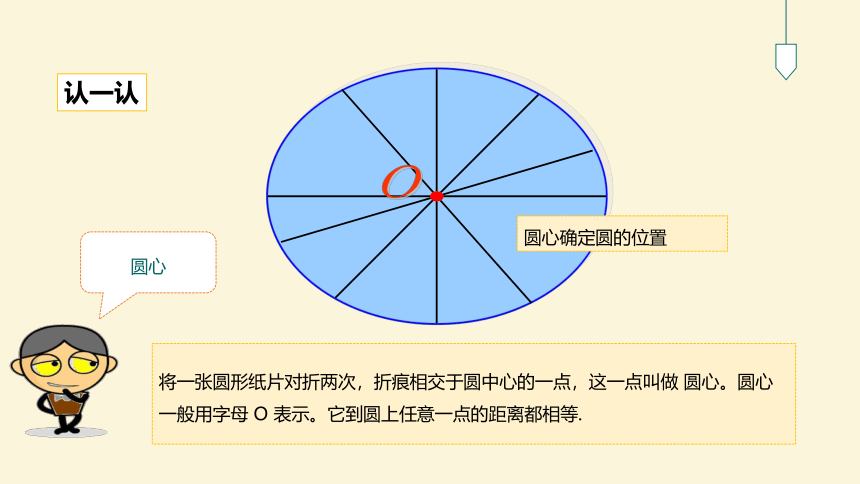
认一认
将一张圆形纸片对折两次,折痕相交于圆中心的一点,这一点叫做
圆心。圆心一般用字母
O
表示。它到圆上任意一点的距离都相等.
圆心确定圆的位置
认一认
o
半径
r
半径:连接圆心到圆上任意一点的线段叫做半径。半径一般用字母
r
表示。把圆规两脚分开,两脚之间的距离就是圆的半径。
半径确定圆的大小
半径
认一认
o
半径
r
直
径
d
直径:通过圆心并且两端都在圆上的线段叫做直径。直径一般用字
母
d
表示。圆内最长的线段是直径。
直径
0
1
2
3
4
6
7
8
5
o
圆心到圆上任意一点的距离都相等。
量一量
想一想
在同一个圆里有多少条半径?
所有的半径都相等吗?
在同一个圆里有多少条直径?
所有的直径都相等吗?
圆的半径和直径有什么关系?
在同一个圆中:直径=半径×2
填表:
为什么车轮都要做成圆的?车轴装在哪里?
想一想
为什么车轮都要做成圆的?车轴装在哪里?
想一想
因为圆心到圆上各点的距离相等,所以圆在
滚动时,圆心在一条直线上运动,这样的车轮运行才稳定。
圆是轴对称图形吗?有几条对称轴?用一个圆形纸片,折一折。
练一练
1
2
3
(1)(
)号线段表示直径。
(2)(
)号线段表示半径。
(3)两端都在圆上的线段中,
(
)最长。
填一填
1
2
3
(1)(
)号线段表示直径。
(2)(
)号线段表示半径。
(3)两端都在圆上的线段中,
(
)最长。
填一填
2
3
直径
(1)半径是射线,直径是直线。(
)
(2)圆的直径都相等。(
)
(3)直径是圆内最长的线段。(
)
(4)圆心决定圆的位置,半径决定圆的大小。(
)
(5)在同一圆里,两条半径就是一条直径。
(
)
(6)以某一点为圆心只能画一个圆。(
)
(7)圆的半径越大,圆就越大。(
)
(8)2个半圆可以拼成一个整圆。(??
?)
对的打“√”
错的打“×”
圆是(
)图形,它有(
)条对称轴;正方形有(
)条对称轴,长方形有(
)条对称轴;半圆有(
)条对称轴,等边三角形有(
)条对称轴,五角星有(
)条对称轴。
练一练
练一练
练一练
1、画一个直径4厘米的圆,那么圆规两脚间的距离应该是(????)厘米。
2、(
)决定圆的大小;(
)决定圆的位置。
3、在长8厘米,宽6厘米的长方形中画一个最大的圆,圆的半径(???)厘米。
4、画圆时,圆规两脚间的距离是圆的(???
????)。
5、时钟的分针转动一周形成的图形是(
????)。
6、在同一个圆中,所有的直径都(?????),所有的半径都(????)。直径是半径的(?????),半径是直径的(?
???)。
7、在边长4厘米的正方形中画一个面积最大的圆,圆的半径是(
)。
综合训练
1、在一张长16厘米,宽8厘米的长方形内画直径是4厘米的圆,这样的圆最多可画(
)个。
2、在一张长50厘米,宽6厘米的长方形纸片中剪最大的圆,这样的圆最多可剪(
)个。
3、在长3分米,宽2分米的长方形上剪出直径是4厘米的圆,至少可以剪(
)个。
4、在长28cm,宽26cm的长方形纸板上剪出一个最大的圆,这个圆的半径是(
)。
能力提升
1、在一张长16厘米,宽8厘米的长方形内画直径是4厘米的圆,这样的圆最多可画(
8
)个。
2、在一张长50厘米,宽6厘米的长方形纸片中剪最大的圆,这样的圆最多可剪(
8
)个。
3、在长3分米,宽2分米的长方形上剪出直径是4厘米的圆,至少可以剪(
35
)个。
4、在长28cm,宽26cm的长方形纸板上剪出一个最大的圆,这个圆的半径是(
13cm
)。
能力提升
能力提升
看图填空:
1.已知下图中长方形中小圆的半径为1cm,则
长方形的长为(?????)cm,宽为(?????)cm。???
2.已知右图中小圆的半径为1cm,?
(1)大圆的直径为(?????)cm。?
(2)正方形的边长为(?????)cm。
1、画一个边长是6厘米的正方形,在这个正方形里面画一个最大的圆形,该怎么做呢??
2、若已知一个圆,怎么在这个圆的内部画一个最大的正方形?
想一想,做一做?
圆心确定圆的位置,半径确定圆的大小
在同一个圆内,所有的半径都相等,所有的直径都相等
在同一个圆内,有无数条半径,有无数条直径
在同一个圆内,直径的长度是半径的
2
倍,半径是直径的一半
用字母表示为:d=2r
r
=
d
圆是轴对称图形,有无数条对称轴。半圆有1条对称轴.
2
1
本课小结
课时结束,下次再会!
圆的认识
温故知新:我们学过哪些几何平面图形?
一起来“找茬”——哪里有圆形?
你知道吗?
一起来玩个游戏吧!
哪种方式更公平呢?
圆的中心到圆上各点的距离都相等
你能想办法画一个圆吗?
画一画,剪一剪。
用圆规画图
0
1
2
3
4
6
7
8
5
画一个半径为2厘米的圆。
一、定长(半径)
二、定点(圆心)
三、一只脚旋转一周
2厘米
折一折
折过若干次后,可以发现什么?
圆心
o
认一认
将一张圆形纸片对折两次,折痕相交于圆中心的一点,这一点叫做
圆心。圆心一般用字母
O
表示。它到圆上任意一点的距离都相等.
圆心确定圆的位置
认一认
o
半径
r
半径:连接圆心到圆上任意一点的线段叫做半径。半径一般用字母
r
表示。把圆规两脚分开,两脚之间的距离就是圆的半径。
半径确定圆的大小
半径
认一认
o
半径
r
直
径
d
直径:通过圆心并且两端都在圆上的线段叫做直径。直径一般用字
母
d
表示。圆内最长的线段是直径。
直径
0
1
2
3
4
6
7
8
5
o
圆心到圆上任意一点的距离都相等。
量一量
想一想
在同一个圆里有多少条半径?
所有的半径都相等吗?
在同一个圆里有多少条直径?
所有的直径都相等吗?
圆的半径和直径有什么关系?
在同一个圆中:直径=半径×2
填表:
为什么车轮都要做成圆的?车轴装在哪里?
想一想
为什么车轮都要做成圆的?车轴装在哪里?
想一想
因为圆心到圆上各点的距离相等,所以圆在
滚动时,圆心在一条直线上运动,这样的车轮运行才稳定。
圆是轴对称图形吗?有几条对称轴?用一个圆形纸片,折一折。
练一练
1
2
3
(1)(
)号线段表示直径。
(2)(
)号线段表示半径。
(3)两端都在圆上的线段中,
(
)最长。
填一填
1
2
3
(1)(
)号线段表示直径。
(2)(
)号线段表示半径。
(3)两端都在圆上的线段中,
(
)最长。
填一填
2
3
直径
(1)半径是射线,直径是直线。(
)
(2)圆的直径都相等。(
)
(3)直径是圆内最长的线段。(
)
(4)圆心决定圆的位置,半径决定圆的大小。(
)
(5)在同一圆里,两条半径就是一条直径。
(
)
(6)以某一点为圆心只能画一个圆。(
)
(7)圆的半径越大,圆就越大。(
)
(8)2个半圆可以拼成一个整圆。(??
?)
对的打“√”
错的打“×”
圆是(
)图形,它有(
)条对称轴;正方形有(
)条对称轴,长方形有(
)条对称轴;半圆有(
)条对称轴,等边三角形有(
)条对称轴,五角星有(
)条对称轴。
练一练
练一练
练一练
1、画一个直径4厘米的圆,那么圆规两脚间的距离应该是(????)厘米。
2、(
)决定圆的大小;(
)决定圆的位置。
3、在长8厘米,宽6厘米的长方形中画一个最大的圆,圆的半径(???)厘米。
4、画圆时,圆规两脚间的距离是圆的(???
????)。
5、时钟的分针转动一周形成的图形是(
????)。
6、在同一个圆中,所有的直径都(?????),所有的半径都(????)。直径是半径的(?????),半径是直径的(?
???)。
7、在边长4厘米的正方形中画一个面积最大的圆,圆的半径是(
)。
综合训练
1、在一张长16厘米,宽8厘米的长方形内画直径是4厘米的圆,这样的圆最多可画(
)个。
2、在一张长50厘米,宽6厘米的长方形纸片中剪最大的圆,这样的圆最多可剪(
)个。
3、在长3分米,宽2分米的长方形上剪出直径是4厘米的圆,至少可以剪(
)个。
4、在长28cm,宽26cm的长方形纸板上剪出一个最大的圆,这个圆的半径是(
)。
能力提升
1、在一张长16厘米,宽8厘米的长方形内画直径是4厘米的圆,这样的圆最多可画(
8
)个。
2、在一张长50厘米,宽6厘米的长方形纸片中剪最大的圆,这样的圆最多可剪(
8
)个。
3、在长3分米,宽2分米的长方形上剪出直径是4厘米的圆,至少可以剪(
35
)个。
4、在长28cm,宽26cm的长方形纸板上剪出一个最大的圆,这个圆的半径是(
13cm
)。
能力提升
能力提升
看图填空:
1.已知下图中长方形中小圆的半径为1cm,则
长方形的长为(?????)cm,宽为(?????)cm。???
2.已知右图中小圆的半径为1cm,?
(1)大圆的直径为(?????)cm。?
(2)正方形的边长为(?????)cm。
1、画一个边长是6厘米的正方形,在这个正方形里面画一个最大的圆形,该怎么做呢??
2、若已知一个圆,怎么在这个圆的内部画一个最大的正方形?
想一想,做一做?
圆心确定圆的位置,半径确定圆的大小
在同一个圆内,所有的半径都相等,所有的直径都相等
在同一个圆内,有无数条半径,有无数条直径
在同一个圆内,直径的长度是半径的
2
倍,半径是直径的一半
用字母表示为:d=2r
r
=
d
圆是轴对称图形,有无数条对称轴。半圆有1条对称轴.
2
1
本课小结
课时结束,下次再会!
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
