北师大版高中数学必修三1.5用样本估计总体 课件(25张ppt)
文档属性
| 名称 | 北师大版高中数学必修三1.5用样本估计总体 课件(25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 344.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 13:43:46 | ||
图片预览







文档简介
(共25张PPT)
样本估计总体
1、频数
将一批数据按照要求分成若干组,各组内数据的个数叫作该组的频数.
2、频率
每组频数除以全体数据的个数的值叫作该组数据的频率.频率反映数据在每组中所占比例的大小.
3、频率分布直方图
在直角坐标系中,横轴表示样本数据,纵轴表示频率与组距的比值,将频率分布表中各组频率的大小用相应矩形面积的大小来表示,由此画成的统计图叫作频率分布直方图.
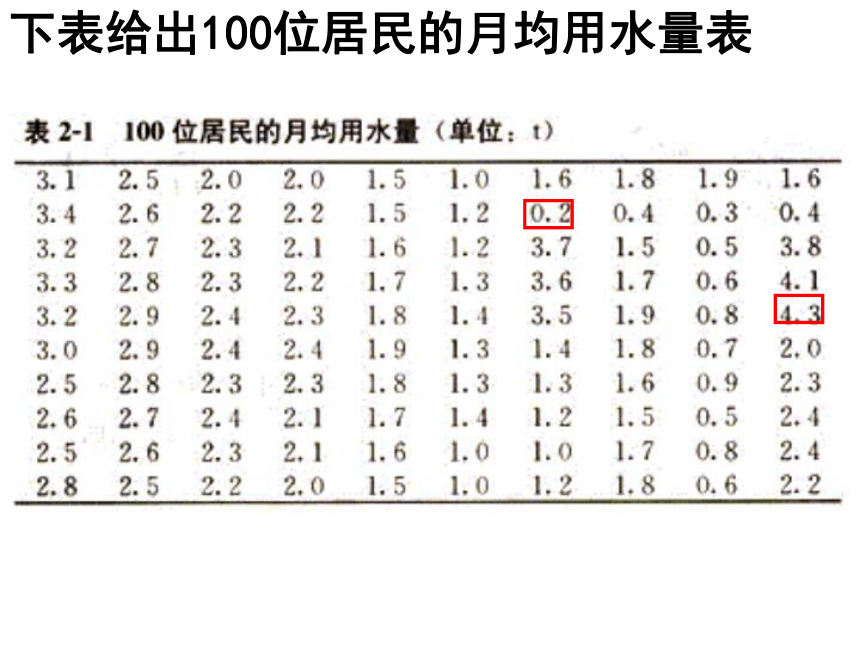
下表给出100位居民的月均用水量表
第一步:
求极差:
(数据组中最大值与最小值的差距)
最大值=
4.3
最小值=
0.2
所以极差=
4.3-0.2
=
4.1
制作频率分布直方图的一般步骤:
第二步:
决定组距与组数:
(强调取整)
当样本容量不超过100时,
按照数据的多少,
常分成5~12组.
为方便组距的选择应力求“取整”.
本题如果组距为0.5(t).
则
所以将数据分成9组较合适.
第三步:
将数据分组:
(
给出组的界限)
[0,
0.5),
[0.5,
1),
[1,
1.5),……[4,
4.5)
共9组.
第四步:
列频率分布表.
分组
频数
频率
频率/组距
[0-0.5)
4
[0.5-1)
8
[1-1.5)
15
[1.5-2)
22
[2-2.5)
25
[2.5-3)
15
[3-3.5)
5
[3.5-4)
4
[4-4.5)
2
合计
100
组距=0.5
0.04
0.08
0.08
0.16
0.3
0.15
0.44
0.22
0.25
0.5
1
2.00
0.02
0.04
0.04
0.08
0.1
0.3
0.15
0.05
0
0.1
0.2
0.3
0.4
0.5
0.6
0.5
1
1.5
2
2.5
3
3.5
4
4.5
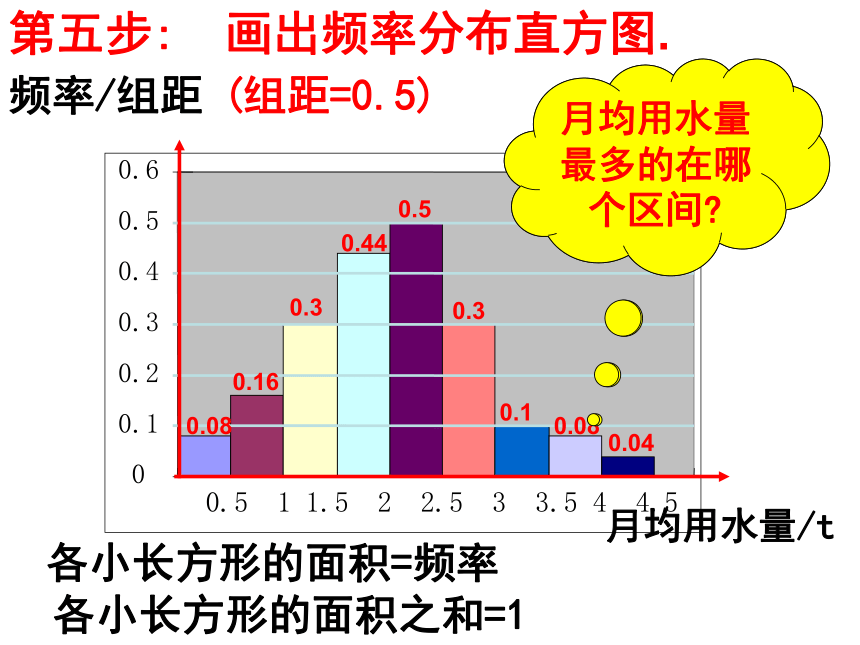
第五步:
画出频率分布直方图.
频率/组距
月均用水量/t
(组距=0.5)
0.08
0.16
0.3
0.44
0.5
0.3
0.1
0.08
0.04
小长方形的面积总和=?
月均用水量最多的在哪个区间?
各小长方形的面积=频率
各小长方形的面积之和=1
0
0.02
54.5
56.5
58.5
60.5
62.5
64.5
66.5
68.5
70.5
72.5
74.5
76.5
体重(kg)
0.04
0.06
0.08
0.10
52.5
78.5
频率分布折线图:
在频率分布直方图中,按照分组原则,再在左边和右边各加一个区间,从所加的左边区间的中点开始,用线段依次连接各个矩形的上端的中点,得到频率分布折线图
0
0.02
54.5
56.5
58.5
60.5
62.5
64.5
66.5
68.5
70.5
72.5
74.5
76.5
体重(kg)
0.04
0.06
0.08
0.10
52.5
78.5
频率折线图
注意:
折线与横轴所围成的面积是1.
频率分布直方图的特征:
从频率分布直方图可以清楚的看出数据分布的总体趋势。
从频率分布直方图得不出原始的数据内容,把数据表示成直方图后,原有的具体数据信息就被抹掉了。
练
习:
1.有一个容量为50的样本数据的分组的频数如下:
[12.5,
15.5)
3
[15.5,
18.5)
8
[18.5,
21.5)
9
[21.5,
24.5)
11
[24.5,
27.5)
10
[27.5,
30.5)
5
[30.5,
33.5)
4
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)根据频率分布直方图估计,数据落在[15.5,
24.5)的百分比是多少?
解:组距为3
分组
频数
频率
频率/
组距
[12.5,
15.5)
3
[15.5,
18.5)
8
[18.5,
21.5)
9
[21.5,
24.5)
11
[24.5,
27.5)
10
[27.5,
30.5)
5
[30.5,
33.5)
4
0.06
0.16
0.18
0.22
0.20
0.10
0.08
0.020
0.053
0.060
0.073
0.067
0.033
0.027
频率分布直方图如下:
频率
组距
0.010
0.020
0.030
0.040
0.050
12.5
15.5
0.060
0.070
练习:2
.投掷一枚均匀骰子44次的记录是:
3
2
4
1
5
1
3
4
5
6
5
4
2
5
3
1
3
4
1
4
5
1
6
3
3
1
2
4
2
6
3
4
6
6
1
6
2
2
5
2
6
5
4
3
现对这些数据进行整理,试画出频数分布直方图.
第一步:写出样本可能出现的一切数值,即:
1,2,3,4,5,6
共6个数.(数据分组)
第二步:列出频率分布表:
样本
1
2
3
4
5
6
频数
7
7
8
8
7
7
频率
0.16
0.16
0.18
0.18
0.16
0.16
组距=1
第三步:
画频率分布直方图
频率
组距
0.1
0.2
0.3
0.4
0.5
O
0.5
1
1.5
2
2.5
3
3.5
4
4.5
月平均用水量(t)
众数在样本数据的频率分布直方图中,
就是最高矩形的中点的横坐标。
如何在频率分布直方图中估计众数
可将众数看作直方图中面积最大长方形的“中心”
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
前四个小矩形的面积和=0.49
后四个小矩形的面积和=0.26
2.02
如何在频率分布直方图中估计中位数
分组
[0,
0.5)
[0.5,
1)
[1,
1.5)
[1.5,
2)
[2,
2.5)
[2.5,
3)
[3,
3.5)
[3.5,
4)
[4,
4.5]
合计
频率
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
1
在样本中中位数的左右各有50%的样本数,
条形面积各为0.5,所以反映在直方图中位数
左右的面积相等.
,
中位数
)
可将中位数看作整个直方图面积的“中心”
思考讨论以下问题:
1、2.02这个中位数的估计值,与样本的中位数值2.0不一样,你能解释其中原因吗?
答:2.02这个中位数的估计值,与样本的中位数值2.0不一样,这是因为样本数据的频率分布直方图,只是直观地表明分布的形状,但是从直方图本身得不出原始的数据内容,直方图已经损失一些样本信息。所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致.
如何在频率分布直方图中估计平均数
=2.02
=2.02
平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。
可将平均数看作整个直方图面积的“重心”
小结:
画频率分布直方图的步骤:
第一步:
求极差:
(数据组中最大值与最小值的差距)
第二步:
决定组距与组数:
(强调取整)
第三步:
将数据分组
(
给出组的界限)
第四步:
列频率分布表.
(包括分组、频数、频率、频率/组距)
第五步:
画频率分布直方图(在频率分布表的基础上绘制,横坐标为样本数据尺寸,纵坐标为频率/组距.)
组距:指每个小组的两个端点的距离,组距
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组。
2.
样本频率分布估计
从频率分布直方图可以清楚的看出数据分布的总体趋势,
但得不出原始数据的内容.
频率分布表
频率分布直方图
频率分布折线图
样本估计总体
1、频数
将一批数据按照要求分成若干组,各组内数据的个数叫作该组的频数.
2、频率
每组频数除以全体数据的个数的值叫作该组数据的频率.频率反映数据在每组中所占比例的大小.
3、频率分布直方图
在直角坐标系中,横轴表示样本数据,纵轴表示频率与组距的比值,将频率分布表中各组频率的大小用相应矩形面积的大小来表示,由此画成的统计图叫作频率分布直方图.
下表给出100位居民的月均用水量表
第一步:
求极差:
(数据组中最大值与最小值的差距)
最大值=
4.3
最小值=
0.2
所以极差=
4.3-0.2
=
4.1
制作频率分布直方图的一般步骤:
第二步:
决定组距与组数:
(强调取整)
当样本容量不超过100时,
按照数据的多少,
常分成5~12组.
为方便组距的选择应力求“取整”.
本题如果组距为0.5(t).
则
所以将数据分成9组较合适.
第三步:
将数据分组:
(
给出组的界限)
[0,
0.5),
[0.5,
1),
[1,
1.5),……[4,
4.5)
共9组.
第四步:
列频率分布表.
分组
频数
频率
频率/组距
[0-0.5)
4
[0.5-1)
8
[1-1.5)
15
[1.5-2)
22
[2-2.5)
25
[2.5-3)
15
[3-3.5)
5
[3.5-4)
4
[4-4.5)
2
合计
100
组距=0.5
0.04
0.08
0.08
0.16
0.3
0.15
0.44
0.22
0.25
0.5
1
2.00
0.02
0.04
0.04
0.08
0.1
0.3
0.15
0.05
0
0.1
0.2
0.3
0.4
0.5
0.6
0.5
1
1.5
2
2.5
3
3.5
4
4.5
第五步:
画出频率分布直方图.
频率/组距
月均用水量/t
(组距=0.5)
0.08
0.16
0.3
0.44
0.5
0.3
0.1
0.08
0.04
小长方形的面积总和=?
月均用水量最多的在哪个区间?
各小长方形的面积=频率
各小长方形的面积之和=1
0
0.02
54.5
56.5
58.5
60.5
62.5
64.5
66.5
68.5
70.5
72.5
74.5
76.5
体重(kg)
0.04
0.06
0.08
0.10
52.5
78.5
频率分布折线图:
在频率分布直方图中,按照分组原则,再在左边和右边各加一个区间,从所加的左边区间的中点开始,用线段依次连接各个矩形的上端的中点,得到频率分布折线图
0
0.02
54.5
56.5
58.5
60.5
62.5
64.5
66.5
68.5
70.5
72.5
74.5
76.5
体重(kg)
0.04
0.06
0.08
0.10
52.5
78.5
频率折线图
注意:
折线与横轴所围成的面积是1.
频率分布直方图的特征:
从频率分布直方图可以清楚的看出数据分布的总体趋势。
从频率分布直方图得不出原始的数据内容,把数据表示成直方图后,原有的具体数据信息就被抹掉了。
练
习:
1.有一个容量为50的样本数据的分组的频数如下:
[12.5,
15.5)
3
[15.5,
18.5)
8
[18.5,
21.5)
9
[21.5,
24.5)
11
[24.5,
27.5)
10
[27.5,
30.5)
5
[30.5,
33.5)
4
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)根据频率分布直方图估计,数据落在[15.5,
24.5)的百分比是多少?
解:组距为3
分组
频数
频率
频率/
组距
[12.5,
15.5)
3
[15.5,
18.5)
8
[18.5,
21.5)
9
[21.5,
24.5)
11
[24.5,
27.5)
10
[27.5,
30.5)
5
[30.5,
33.5)
4
0.06
0.16
0.18
0.22
0.20
0.10
0.08
0.020
0.053
0.060
0.073
0.067
0.033
0.027
频率分布直方图如下:
频率
组距
0.010
0.020
0.030
0.040
0.050
12.5
15.5
0.060
0.070
练习:2
.投掷一枚均匀骰子44次的记录是:
3
2
4
1
5
1
3
4
5
6
5
4
2
5
3
1
3
4
1
4
5
1
6
3
3
1
2
4
2
6
3
4
6
6
1
6
2
2
5
2
6
5
4
3
现对这些数据进行整理,试画出频数分布直方图.
第一步:写出样本可能出现的一切数值,即:
1,2,3,4,5,6
共6个数.(数据分组)
第二步:列出频率分布表:
样本
1
2
3
4
5
6
频数
7
7
8
8
7
7
频率
0.16
0.16
0.18
0.18
0.16
0.16
组距=1
第三步:
画频率分布直方图
频率
组距
0.1
0.2
0.3
0.4
0.5
O
0.5
1
1.5
2
2.5
3
3.5
4
4.5
月平均用水量(t)
众数在样本数据的频率分布直方图中,
就是最高矩形的中点的横坐标。
如何在频率分布直方图中估计众数
可将众数看作直方图中面积最大长方形的“中心”
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
前四个小矩形的面积和=0.49
后四个小矩形的面积和=0.26
2.02
如何在频率分布直方图中估计中位数
分组
[0,
0.5)
[0.5,
1)
[1,
1.5)
[1.5,
2)
[2,
2.5)
[2.5,
3)
[3,
3.5)
[3.5,
4)
[4,
4.5]
合计
频率
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
1
在样本中中位数的左右各有50%的样本数,
条形面积各为0.5,所以反映在直方图中位数
左右的面积相等.
,
中位数
)
可将中位数看作整个直方图面积的“中心”
思考讨论以下问题:
1、2.02这个中位数的估计值,与样本的中位数值2.0不一样,你能解释其中原因吗?
答:2.02这个中位数的估计值,与样本的中位数值2.0不一样,这是因为样本数据的频率分布直方图,只是直观地表明分布的形状,但是从直方图本身得不出原始的数据内容,直方图已经损失一些样本信息。所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致.
如何在频率分布直方图中估计平均数
=2.02
=2.02
平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。
可将平均数看作整个直方图面积的“重心”
小结:
画频率分布直方图的步骤:
第一步:
求极差:
(数据组中最大值与最小值的差距)
第二步:
决定组距与组数:
(强调取整)
第三步:
将数据分组
(
给出组的界限)
第四步:
列频率分布表.
(包括分组、频数、频率、频率/组距)
第五步:
画频率分布直方图(在频率分布表的基础上绘制,横坐标为样本数据尺寸,纵坐标为频率/组距.)
组距:指每个小组的两个端点的距离,组距
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组。
2.
样本频率分布估计
从频率分布直方图可以清楚的看出数据分布的总体趋势,
但得不出原始数据的内容.
频率分布表
频率分布直方图
频率分布折线图
