北师大版数学七年级上册4.2 比较线段的长短 课件(43张)
文档属性
| 名称 | 北师大版数学七年级上册4.2 比较线段的长短 课件(43张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 698.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 00:00:00 | ||
图片预览





文档简介
4.2 比较线段的长短
如何比较两个人的身高?
我身高1.53米,
比你高3厘米.
我身高1.5米.
导入新知
看下面这三幅图片谁高谁矮?你是依据什么判断的 ?
导入新知
1. 了解两点间距离的意义,理解“两点之间,线段最短”的线段性质,并学会运用.
.
2. 会用尺规画一条线段等于已知线段,会比较两条线段的长短.
素养目标
3. 理解线段中点、等分点的意义,能够运用线段的和、差、倍、分关系求线段的长度.
A
F
E
D
B
C
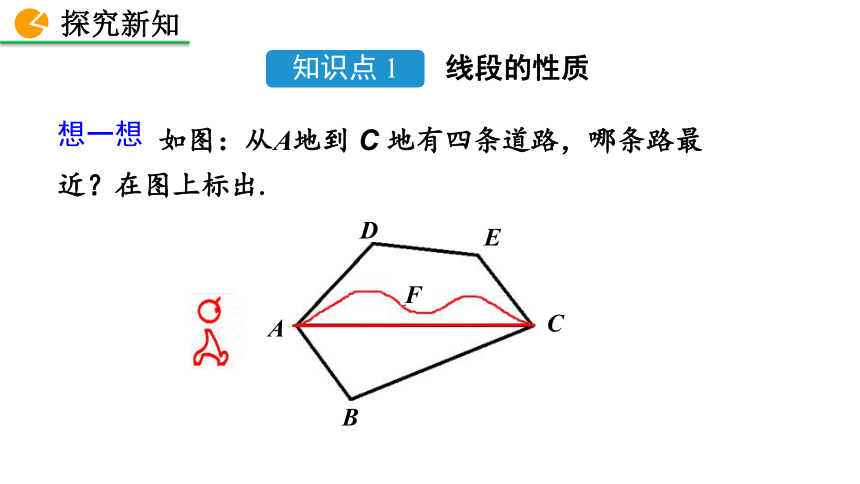
如图:从A地到 C 地有四条道路,哪条路最 近?在图上标出.
线段的性质
知识点 1
探究新知
想一想
A
F
E
D
B
C
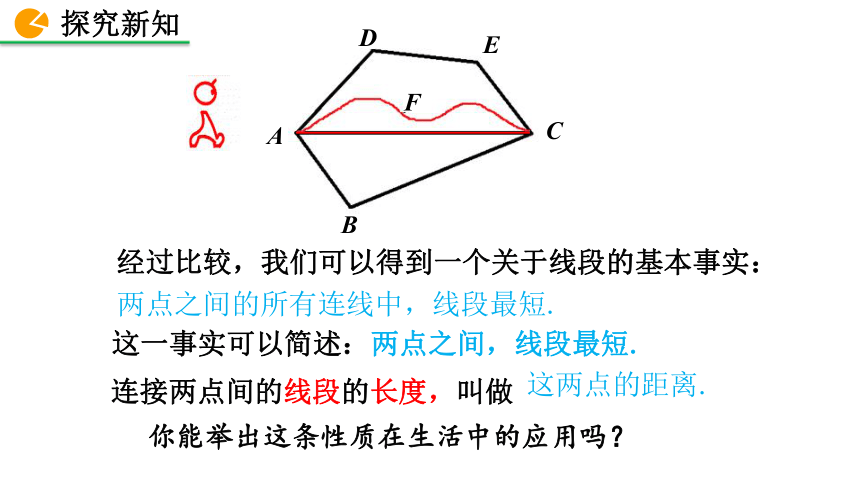
经过比较,我们可以得到一个关于线段的基本事实:
两点之间的所有连线中,线段最短.
连接两点间的线段的长度,叫做
这两点的距离.
你能举出这条性质在生活中的应用吗?
这一事实可以简述:两点之间,线段最短.
探究新知
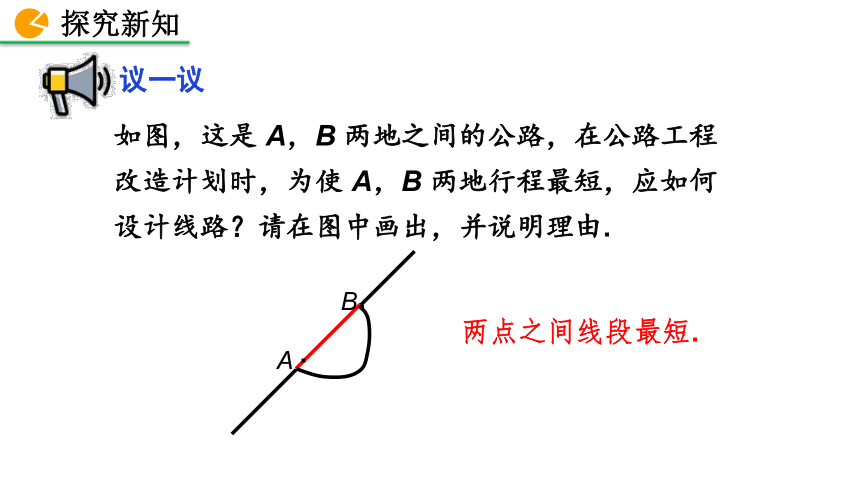
两点之间线段最短.
如图,这是 A,B 两地之间的公路,在公路工程
改造计划时,为使 A,B 两地行程最短,应如何
设计线路?请在图中画出,并说明理由.
.
B
A
.
探究新知
议一议
把原来弯曲的河道改直,A,B 两地间的河道长
度有什么变化?
A
B
A,B 两地间的河道长度变短.
探究新知
想一想
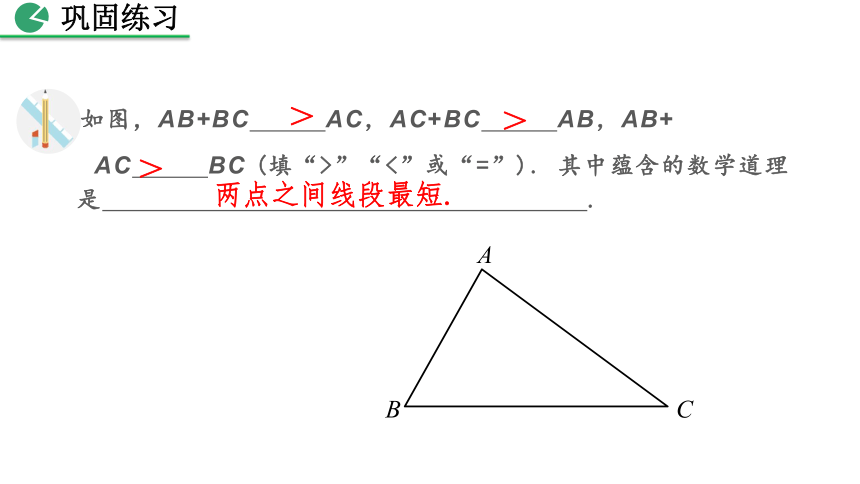
如图,AB+BC AC,AC+BC AB,AB+
AC BC (填“>”“<”或“=”). 其中蕴含的数学道理是 .
>
两点之间线段最短.
>
>
A
B
C
巩固练习
在一条笔直的公路两侧,分别有 A,B 两个村庄,
如图,现在要在公路 l 上建一个汽车站 C,使汽
车站到 A,B 两村庄的距离之和最小,请在图中
画出汽车站的位置.
C
A
B
l
巩固练习
比较下图哪棵树高?哪支铅笔长?窗框相邻的两条边哪条边长?你是怎么比较的?
探究新知
知识点 2
线段的比较
如何比较两条线段的长短呢?
思考
猜想交流
观察这三组图形,你能比较出每组图形中线段 a 和 b 的长短吗?
三组图形中,线段a与b的长度均相等
很多时候,眼见未必为实. 准确比较线段的长短还需要更加严谨的办法.
(1)
(2)
(3)
a
b
a
a
b
b
探究新知
合作探究
做手工时,在没有刻度尺的条件下,若想从较长的木棍上截下一段,使截下的木棒等于另一根短木棒的长,我们常采用以上办法.
探究新知
画在黑板上的线段是无法移动的,在只有圆规和无刻度的直尺的情况下,请大家想想办法,如何再画一条与它相等的线段?
思考
小提示:在可打开角度的最大范围内,圆规可截取任意长度,相当于可以移动的“小木棍”.
探究新知
你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?
讨论
160cm
170cm
探究新知
比较两个同学高矮的方法:
——叠合法.
②让两个同学站在同一平地上,脚底平齐,观看
两人的头顶,直接比出高矮.
①用卷尺分别度量出两个同学的身高,将所得的
数值进行比较.
——度量法.
探究新知
D
C
B
试比较线段AB,CD 的长短.
(1) 度量法;
(2) 叠合法
将其中一条线段“移”到另一条线段上,使其一端点与另一线段的一端点重合,然后观察两条线段另外两个端点的位置作比较.
(A)
C D
A B
探究新知
C
D
1. 若点 A 与点 C 重合,点 B 落
在C,D之间,那么 AB CD.
(A)
B
<
叠合法结论:
C
D
A
B
B
(A)
2. 若点 A 与点 C 重合,点 B 与
点 D ,那么 AB = CD.
3. 若点 A 与点 C 重合,点 B 落在 CD 的延长线上,那么 AB
CD.
重合
>
B
A
B
A
C
D
(A)
(B)
探究新知
1.为了比较线段AB与CD的大小,小明将点A与点C重合使两条线段在一条直线上,结果点B在CD的延长线上,则( )
A.AB<CD B.AB>CD
C.AB=CD D.以上都不对
2.如图所示,AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD C.AC=BD D.无法确定
B
C
巩固练习
已知线段AB,用尺规作一条线段等于已知线段 AB.
A
B
①先作一条射线A 'C ';
A '
C '
②用圆规量取已知线段AB的长度;
③在射线上截取A 'B ' =AB,线段A 'B '就是 所求的线段.
探究新知
作一条线段等于已知线段(尺规作图法)
知识点 3
例
在直线上画出线段 AB=a?,再在 AB 的延长线上画线段BC=b,线段AC 就是 与 的和,记作 AC= . 如果在AB上画线段 BD=b,那么线段 AD 就是 与 的差,记作AD= .
A
B
C
D
a+b
a-b
a
b
b
画一画
a
b
a+b
a
b
a-b
探究新知
1.如图,点B,C在线段 AD 上则AB+BC=____; AD-CD=___;BC= ___ -___= ___ - ___.
A
B
C
D
AC
AC
AC
AB
BD
CD
2.如图,已知线段a,b,画一条线段AB,使
AB=2a-b.
a
b
A
B
2a-b
2a
b
巩固练习
在一张纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点处于线段的什么位置?
A
B
M
探究新知
知识点 4
线段的中点
A
B
M
如图,点M 把线段 AB 分成相等的两条线段AM 与BM,点 M 叫做线段AB 的中点.类似地,还有线段的三等分点、四等分点等.
线段的三等分点
线段的四等分点
探究新知
A
a
a
M
B
M 是线段AB的中点
几何语言:因为 M 是线段 AB 的中点,
所以 AM = MB = AB.
( 或AB =2AM = 2MB )
反之也成立:因为 AM = MB = AB
( 或AB =2AM =2MB ),
所以 M是线段 AB 的中点.
探究新知
点M , N 是线段AB的三等分点:
AM = MN = NB = ___ AB
(或 AB = ___AM = ___ MN = ___NB)
3
3
3
N
M
B
A
探究新知
例1 若 AB = 6cm,点 C 是线段 AB 的中点,点 D是线段 CB 的中点,求:线段 AD 的长是多少?
解:因为 C 是线段AB的中点,
因为 D 是线段CB 的中点,
所以AC = CB = AB = ×6= 3 (cm).
所以 CD = CB = ×3=1.5 (cm).
所以 AD =AC + CD = 3 + 1.5 = 4.5 (cm).
A C B
D
利用中点求线段的长度
探究新知
素养考点 1
1.如图,点C 是线段AB 的中点,若AB = 8 cm,
则AC = cm.
4
C
A
C
B
2.如图,下列说法,不能判断点C 是线段AB 的中点的是 ( )
A. AC = CB B. AB = 2 AC
C. AC + CB = AB D. CB = AB
A
C
B
巩固练习
变式训练
3.如图,线段AB =4 cm,BC = 6 cm,若点D为线段AB 的中点,点E为线段 BC 的中点,求线段 DE 的长.
A D B E C
答案:DE 的长为 5 cm.
巩固练习
变式训练
例2 如图,B,C是线段AD上两点,且AB:BC:CD=
3:2:5,E,F分别是AB,CD的中点,且EF=24,求线段AB,BC,CD的长.
F
E
C
B
D
A
解析:根据已知条件AB:BC:CD=3:2:5,不妨设AB=3x,BC =2x,CD=5x,然后运用线段的和差倍分,用含x的代数式表示EF的长,从而得到一个关于x的一元一次方程,解方程,得到x的值,即可得到所求各线段的长.
利用比例或倍分关系求线段的长度
探究新知
素养考点 2
F
E
C
B
D
A
解:设AB=3x,BC=2x,CD=5x,
因为E,F分别是AB,CD的中点,
所以
所以EF=BE+BC+CF=
因为EF=24,所以6x=24,解得x=4.
所以AB=3x=12,BC=2x=8,CD=5x=20.
探究新知
求线段的长度时,当题目中涉及到线段长度的比例或倍分关系时,通常可以设未知数,运用方程思想求解.
探究新知
方法点拨
如图,已知线段AB和CD的公共部分BD= AB= CD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.
F
E
B
D
C
A
解析:根据已知条件,不妨设BD=xcm,则AB=3xcm,CD=4xcm,易得AC=6xcm.在由线段中点的定义及线段的和差关系,用含x的代数式表示EF的长,从而得到一个一元一次方程,求解即可.
巩固练习
变式训练
解:设BD=xcm,则AB=3xcm,CD=4xcm,AC =6xcm,
因为E,F分别是AB,CD的中点,
所以
所以EF=AC-AE-CF=
所以AB=3xcm=12cm,CD=4xcm=16cm.
F
E
B
D
C
A
因为EF=10,所以 x=10,解得x=4.
巩固练习
例3 A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )
A.1cm B.9cm C.1cm或9cm D.以上答案都不对
解析:分以下两种情况进行讨论:?当点C在AB之间上,故AC=AB-BC=1cm;?当点C在AB的延长线上时,AC=AB+BC=9cm.
C
方法总结:无图时求线段的长,应注意分类讨论,一般分以下两种情况:?点在某一线段上;?点在该线段的延长线.
需要分类讨论的问题
探究新知
素养考点 3
已知A,B,C三点共线,线段AB=25cm,BC=16cm,点E,F分别是线段AB,BC的中点,则线段EF的长为( )
A.21cm或4cm B.20.5cm
C.4.5cm D.20.5cm或4.5cm
D
巩固练习
变式训练
(2019?吉林)曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光.如图,A、B两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( )
A.两点之间,线段最短
B.平行于同一条直线的两条直线平行
C.垂线段最短
D.两点确定一条直线
A
连接中考
1. 下列说法正确的是 ( )
A. 两点间距离的定义是指两点之间的线段
B. 两点之间的距离是指两点之间的直线
C. 两点之间的距离是指连接两点之间线段的长度
D. 两点之间的距离是两点之间的直线的长度
2. 如图,AC = DB,则图中另外两条相等的线段为_____________.
C
A C D B
AD=BC
基础巩固题
课堂检测
3.已知线段 AB = 6 cm,延长 AB 到C,使BC = 2AB,若 D为AB 的中点,则线段DC 的长为________.
C
A
D
B
15 cm
4.点A,B,C在同一条数轴上,其中点A,B表示的数分别是-3,1,若BC=5,则AC=_________.
9或1
课堂检测
基础巩固题
如图:AB = 4 cm,BC = 3 cm,如果点O 是线段 AC 的中点.求线段 OB 的长度.
A
B
C
O
解:因为 AC = AB + BC = 4+3=7 (cm),
点O 为线段 AC 的中点,
所以 OC = AC= ×7 = 3.5 (cm),
所以OB = OC-BC = 3.5-3 = 0.5 (cm).
能力提升题
课堂检测
已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6,求CM和AD的长.
D
A
C
B
M
AD=10x=20 .
解:设AB=2x,BC=5x,CD=3x,
所以AD=AB+BC+CD=10x.
因为M是AD的中点,
所以AM=MD=5x,
所以BM=AM-AB=3x.
因为BM=6,
即3x=6,所以x=2.
故CM=MD-CD=2x=4,
拓广探索题
课堂检测
比较线段的长短
线段长短的比较
线段的性质
线段中点的概念
度量法
叠合法
两点之间线段最短
课堂小结
尺规作图法
把一条线段分成相等的两条线段的点,叫做线段的中点
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
如何比较两个人的身高?
我身高1.53米,
比你高3厘米.
我身高1.5米.
导入新知
看下面这三幅图片谁高谁矮?你是依据什么判断的 ?
导入新知
1. 了解两点间距离的意义,理解“两点之间,线段最短”的线段性质,并学会运用.
.
2. 会用尺规画一条线段等于已知线段,会比较两条线段的长短.
素养目标
3. 理解线段中点、等分点的意义,能够运用线段的和、差、倍、分关系求线段的长度.
A
F
E
D
B
C
如图:从A地到 C 地有四条道路,哪条路最 近?在图上标出.
线段的性质
知识点 1
探究新知
想一想
A
F
E
D
B
C
经过比较,我们可以得到一个关于线段的基本事实:
两点之间的所有连线中,线段最短.
连接两点间的线段的长度,叫做
这两点的距离.
你能举出这条性质在生活中的应用吗?
这一事实可以简述:两点之间,线段最短.
探究新知
两点之间线段最短.
如图,这是 A,B 两地之间的公路,在公路工程
改造计划时,为使 A,B 两地行程最短,应如何
设计线路?请在图中画出,并说明理由.
.
B
A
.
探究新知
议一议
把原来弯曲的河道改直,A,B 两地间的河道长
度有什么变化?
A
B
A,B 两地间的河道长度变短.
探究新知
想一想
如图,AB+BC AC,AC+BC AB,AB+
AC BC (填“>”“<”或“=”). 其中蕴含的数学道理是 .
>
两点之间线段最短.
>
>
A
B
C
巩固练习
在一条笔直的公路两侧,分别有 A,B 两个村庄,
如图,现在要在公路 l 上建一个汽车站 C,使汽
车站到 A,B 两村庄的距离之和最小,请在图中
画出汽车站的位置.
C
A
B
l
巩固练习
比较下图哪棵树高?哪支铅笔长?窗框相邻的两条边哪条边长?你是怎么比较的?
探究新知
知识点 2
线段的比较
如何比较两条线段的长短呢?
思考
猜想交流
观察这三组图形,你能比较出每组图形中线段 a 和 b 的长短吗?
三组图形中,线段a与b的长度均相等
很多时候,眼见未必为实. 准确比较线段的长短还需要更加严谨的办法.
(1)
(2)
(3)
a
b
a
a
b
b
探究新知
合作探究
做手工时,在没有刻度尺的条件下,若想从较长的木棍上截下一段,使截下的木棒等于另一根短木棒的长,我们常采用以上办法.
探究新知
画在黑板上的线段是无法移动的,在只有圆规和无刻度的直尺的情况下,请大家想想办法,如何再画一条与它相等的线段?
思考
小提示:在可打开角度的最大范围内,圆规可截取任意长度,相当于可以移动的“小木棍”.
探究新知
你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?
讨论
160cm
170cm
探究新知
比较两个同学高矮的方法:
——叠合法.
②让两个同学站在同一平地上,脚底平齐,观看
两人的头顶,直接比出高矮.
①用卷尺分别度量出两个同学的身高,将所得的
数值进行比较.
——度量法.
探究新知
D
C
B
试比较线段AB,CD 的长短.
(1) 度量法;
(2) 叠合法
将其中一条线段“移”到另一条线段上,使其一端点与另一线段的一端点重合,然后观察两条线段另外两个端点的位置作比较.
(A)
C D
A B
探究新知
C
D
1. 若点 A 与点 C 重合,点 B 落
在C,D之间,那么 AB CD.
(A)
B
<
叠合法结论:
C
D
A
B
B
(A)
2. 若点 A 与点 C 重合,点 B 与
点 D ,那么 AB = CD.
3. 若点 A 与点 C 重合,点 B 落在 CD 的延长线上,那么 AB
CD.
重合
>
B
A
B
A
C
D
(A)
(B)
探究新知
1.为了比较线段AB与CD的大小,小明将点A与点C重合使两条线段在一条直线上,结果点B在CD的延长线上,则( )
A.AB<CD B.AB>CD
C.AB=CD D.以上都不对
2.如图所示,AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD C.AC=BD D.无法确定
B
C
巩固练习
已知线段AB,用尺规作一条线段等于已知线段 AB.
A
B
①先作一条射线A 'C ';
A '
C '
②用圆规量取已知线段AB的长度;
③在射线上截取A 'B ' =AB,线段A 'B '就是 所求的线段.
探究新知
作一条线段等于已知线段(尺规作图法)
知识点 3
例
在直线上画出线段 AB=a?,再在 AB 的延长线上画线段BC=b,线段AC 就是 与 的和,记作 AC= . 如果在AB上画线段 BD=b,那么线段 AD 就是 与 的差,记作AD= .
A
B
C
D
a+b
a-b
a
b
b
画一画
a
b
a+b
a
b
a-b
探究新知
1.如图,点B,C在线段 AD 上则AB+BC=____; AD-CD=___;BC= ___ -___= ___ - ___.
A
B
C
D
AC
AC
AC
AB
BD
CD
2.如图,已知线段a,b,画一条线段AB,使
AB=2a-b.
a
b
A
B
2a-b
2a
b
巩固练习
在一张纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点处于线段的什么位置?
A
B
M
探究新知
知识点 4
线段的中点
A
B
M
如图,点M 把线段 AB 分成相等的两条线段AM 与BM,点 M 叫做线段AB 的中点.类似地,还有线段的三等分点、四等分点等.
线段的三等分点
线段的四等分点
探究新知
A
a
a
M
B
M 是线段AB的中点
几何语言:因为 M 是线段 AB 的中点,
所以 AM = MB = AB.
( 或AB =2AM = 2MB )
反之也成立:因为 AM = MB = AB
( 或AB =2AM =2MB ),
所以 M是线段 AB 的中点.
探究新知
点M , N 是线段AB的三等分点:
AM = MN = NB = ___ AB
(或 AB = ___AM = ___ MN = ___NB)
3
3
3
N
M
B
A
探究新知
例1 若 AB = 6cm,点 C 是线段 AB 的中点,点 D是线段 CB 的中点,求:线段 AD 的长是多少?
解:因为 C 是线段AB的中点,
因为 D 是线段CB 的中点,
所以AC = CB = AB = ×6= 3 (cm).
所以 CD = CB = ×3=1.5 (cm).
所以 AD =AC + CD = 3 + 1.5 = 4.5 (cm).
A C B
D
利用中点求线段的长度
探究新知
素养考点 1
1.如图,点C 是线段AB 的中点,若AB = 8 cm,
则AC = cm.
4
C
A
C
B
2.如图,下列说法,不能判断点C 是线段AB 的中点的是 ( )
A. AC = CB B. AB = 2 AC
C. AC + CB = AB D. CB = AB
A
C
B
巩固练习
变式训练
3.如图,线段AB =4 cm,BC = 6 cm,若点D为线段AB 的中点,点E为线段 BC 的中点,求线段 DE 的长.
A D B E C
答案:DE 的长为 5 cm.
巩固练习
变式训练
例2 如图,B,C是线段AD上两点,且AB:BC:CD=
3:2:5,E,F分别是AB,CD的中点,且EF=24,求线段AB,BC,CD的长.
F
E
C
B
D
A
解析:根据已知条件AB:BC:CD=3:2:5,不妨设AB=3x,BC =2x,CD=5x,然后运用线段的和差倍分,用含x的代数式表示EF的长,从而得到一个关于x的一元一次方程,解方程,得到x的值,即可得到所求各线段的长.
利用比例或倍分关系求线段的长度
探究新知
素养考点 2
F
E
C
B
D
A
解:设AB=3x,BC=2x,CD=5x,
因为E,F分别是AB,CD的中点,
所以
所以EF=BE+BC+CF=
因为EF=24,所以6x=24,解得x=4.
所以AB=3x=12,BC=2x=8,CD=5x=20.
探究新知
求线段的长度时,当题目中涉及到线段长度的比例或倍分关系时,通常可以设未知数,运用方程思想求解.
探究新知
方法点拨
如图,已知线段AB和CD的公共部分BD= AB= CD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.
F
E
B
D
C
A
解析:根据已知条件,不妨设BD=xcm,则AB=3xcm,CD=4xcm,易得AC=6xcm.在由线段中点的定义及线段的和差关系,用含x的代数式表示EF的长,从而得到一个一元一次方程,求解即可.
巩固练习
变式训练
解:设BD=xcm,则AB=3xcm,CD=4xcm,AC =6xcm,
因为E,F分别是AB,CD的中点,
所以
所以EF=AC-AE-CF=
所以AB=3xcm=12cm,CD=4xcm=16cm.
F
E
B
D
C
A
因为EF=10,所以 x=10,解得x=4.
巩固练习
例3 A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )
A.1cm B.9cm C.1cm或9cm D.以上答案都不对
解析:分以下两种情况进行讨论:?当点C在AB之间上,故AC=AB-BC=1cm;?当点C在AB的延长线上时,AC=AB+BC=9cm.
C
方法总结:无图时求线段的长,应注意分类讨论,一般分以下两种情况:?点在某一线段上;?点在该线段的延长线.
需要分类讨论的问题
探究新知
素养考点 3
已知A,B,C三点共线,线段AB=25cm,BC=16cm,点E,F分别是线段AB,BC的中点,则线段EF的长为( )
A.21cm或4cm B.20.5cm
C.4.5cm D.20.5cm或4.5cm
D
巩固练习
变式训练
(2019?吉林)曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光.如图,A、B两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( )
A.两点之间,线段最短
B.平行于同一条直线的两条直线平行
C.垂线段最短
D.两点确定一条直线
A
连接中考
1. 下列说法正确的是 ( )
A. 两点间距离的定义是指两点之间的线段
B. 两点之间的距离是指两点之间的直线
C. 两点之间的距离是指连接两点之间线段的长度
D. 两点之间的距离是两点之间的直线的长度
2. 如图,AC = DB,则图中另外两条相等的线段为_____________.
C
A C D B
AD=BC
基础巩固题
课堂检测
3.已知线段 AB = 6 cm,延长 AB 到C,使BC = 2AB,若 D为AB 的中点,则线段DC 的长为________.
C
A
D
B
15 cm
4.点A,B,C在同一条数轴上,其中点A,B表示的数分别是-3,1,若BC=5,则AC=_________.
9或1
课堂检测
基础巩固题
如图:AB = 4 cm,BC = 3 cm,如果点O 是线段 AC 的中点.求线段 OB 的长度.
A
B
C
O
解:因为 AC = AB + BC = 4+3=7 (cm),
点O 为线段 AC 的中点,
所以 OC = AC= ×7 = 3.5 (cm),
所以OB = OC-BC = 3.5-3 = 0.5 (cm).
能力提升题
课堂检测
已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6,求CM和AD的长.
D
A
C
B
M
AD=10x=20 .
解:设AB=2x,BC=5x,CD=3x,
所以AD=AB+BC+CD=10x.
因为M是AD的中点,
所以AM=MD=5x,
所以BM=AM-AB=3x.
因为BM=6,
即3x=6,所以x=2.
故CM=MD-CD=2x=4,
拓广探索题
课堂检测
比较线段的长短
线段长短的比较
线段的性质
线段中点的概念
度量法
叠合法
两点之间线段最短
课堂小结
尺规作图法
把一条线段分成相等的两条线段的点,叫做线段的中点
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
