北师大版七年级上册数学课件: 5.6应用一元一次方程—追赶小明(29张)
文档属性
| 名称 | 北师大版七年级上册数学课件: 5.6应用一元一次方程—追赶小明(29张) |  | |
| 格式 | ppt | ||
| 文件大小 | 850.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 21:46:02 | ||
图片预览






文档简介
竹排的行程问题:
若冬子追赶红军部队至A地,此时部队在冬子前方210千米处,且于25千米/时的速度继续前行,于是冬子选择路边同方向的水路追赶。已知冬子所乘竹排的速度为55千米/时,你能帮冬子算出他需要几小时追上部队吗?
做一做
1.若小明每秒跑4米,那么他20秒能跑( )米.
80
S=v t
路程=速度 X 时间
做一做
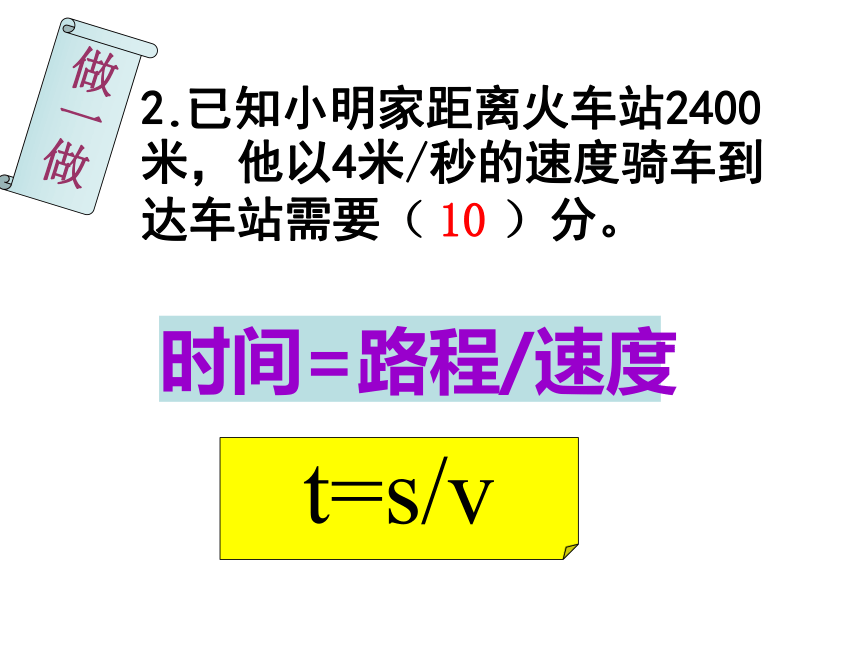
2.已知小明家距离火车站2400米,他以4米/秒的速度骑车到达车站需要( )分。
t=s/v
时间=路程/速度
10
做一做
3.小明用2分钟绕学校操场跑了两圈(每圈300米),那么他的速度为( )米/秒.
速度=路程/时间
v=s/t
5
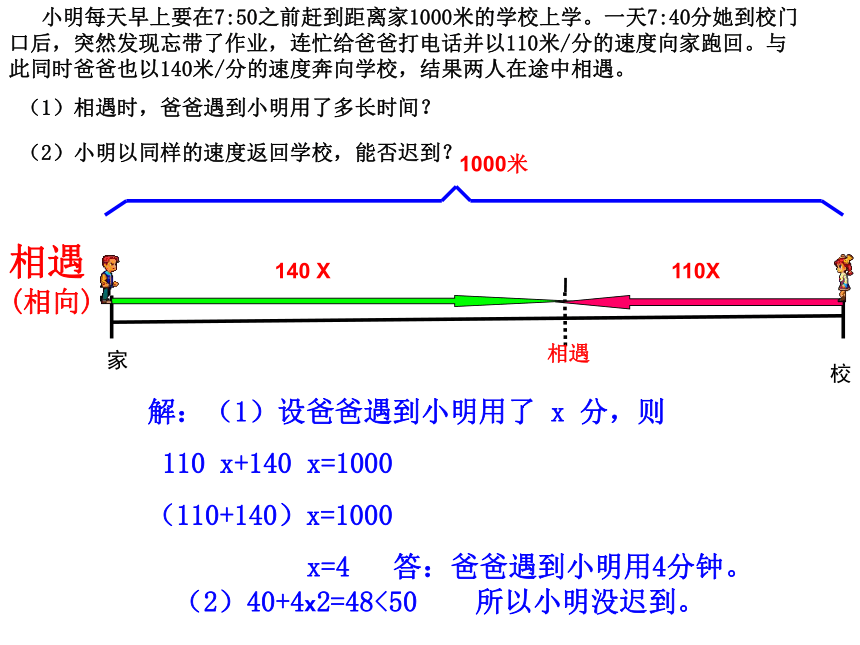
(1)相遇时,爸爸遇到小明用了多长时间?
(2)小明以同样的速度返回学校,能否迟到?
小明每天早上要在7:50分之前赶到距离家1000米的学校上学。一天7:40分她到校门口后,突然发现忘带了作业,连忙给爸爸打电话并以110米/分的速度向家跑回。与此同时爸爸也以140米/分的速度奔向学校,结果两人在途中相遇。
严谨认真
解:(1)设爸爸遇到小明用了 x 分,则
110 x+140 x=1000
(110+140)x=1000
x=4 答:爸爸遇到小明用4分钟。
(2)40+4x2=48<50 所以小明没迟到。
小明每天早上要在7:50之前赶到距离家1000米的学校上学。一天7:40分她到校门口后,突然发现忘带了作业,连忙给爸爸打电话并以110米/分的速度向家跑回。与此同时爸爸也以140米/分的速度奔向学校,结果两人在途中相遇。
(1)相遇时,爸爸遇到小明用了多长时间?
(2)小明以同样的速度返回学校,能否迟到?
相遇
(相向)
家
校
相遇
140 X 110X
1000米
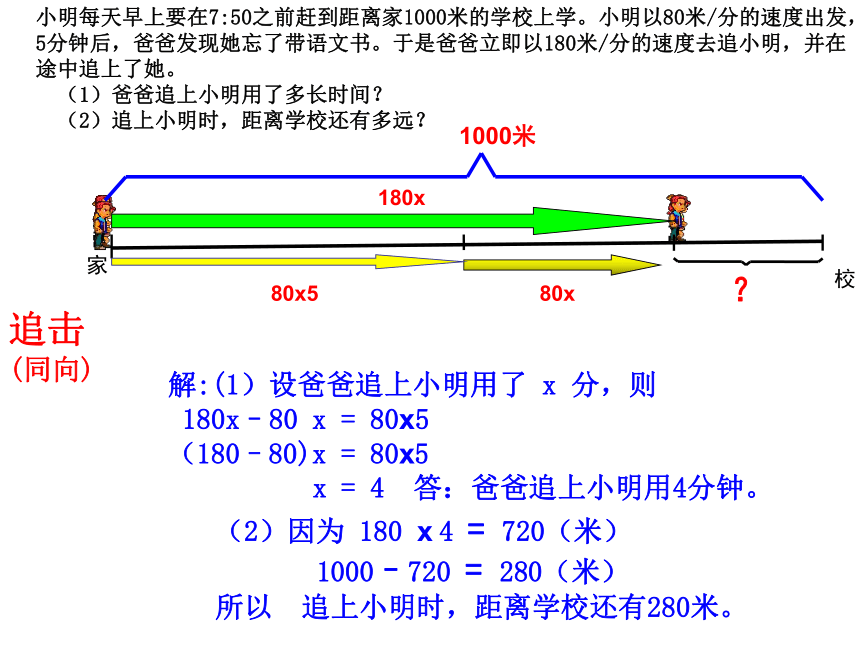
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
小明每天早上要在7:50之前赶到距离家1000米的学校上学。小明以80米/分的速度出发,5分钟后,爸爸发现她忘了带语文书。又是爸爸立即以180米/分的速度去追小明,并在途中追上了她。
严谨认真
解:(1)设爸爸追上小明用了 x 分,则
180x–80 x = 80x5
(180–80)x = 80x5
x = 4 答:爸爸追上小明用4分钟。
(2)因为 180 x 4 = 720(米)
1000–720 = 280(米)
所以 追上小明时,距离学校还有280米。
小明每天早上要在7:50之前赶到距离家1000米的学校上学。小明以80米/分的速度出发,5分钟后,爸爸发现她忘了带语文书。于是爸爸立即以180米/分的速度去追小明,并在途中追上了她。
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
追击
(同向)
1000米
80x5 80x ?
180x
家
校
竹排的行程问题:
若冬子追赶红军部队至A地,此时部队在冬子前方210千米处,且于25千米/时的速度继续前行,于是冬子选择路边同方向的水路追赶。已知冬子所乘竹排的速度为55千米/时,你能帮冬子算出他需要几小时追上部队吗?
竹排的行程问题:
解:设冬子乘竹排需小时追上部队,
由题意得 55X-25X=210
30X=210
X=7
答:冬子追上部队需7小时。
1、行程问题中的相等关系是:路程=速度×时间.
2、相遇问题常用的等量关系:
3、追击问题常用的等量关系:
4、(1)解应用题要学会借助线段图来分析数量关系。
(2)学会文字语言、图形语言、符号语言的互相渗 透,互相转换。
S距=S快+S慢
S距=S快-S慢
即 S快=S距+S慢
1.小彬和小明跑步,小彬每秒跑4米,小明每秒跑6米。(1)若他们站在百米跑道的两端同时相向起跑,几秒后两人相遇?(2)若小明站在跑道的起点处,小彬站在他前面10米处,两人同时同向起跑,几秒后小明能追上小彬?
随堂练习
(2)设x秒后甲追上乙,根据题意得
6x-4x=10
解:(1)设x秒后两人相遇,根据题意得
6x+4x=100
只列方程不解
2.甲乙两地相距230千米,一辆卡车和一货客 车分别以50千米/时和40千米/时的速度从两地出发,相向而行,若卡车早出发1小时,则卡车再行几小时两车相遇?
解:设卡车行X小时两车相遇,
由题意得 50 + 50X+40X=230
50(1+X)+40X=230
90X=180
X=2
答:卡车行2小时两车相遇。
问题1:后队追上前队用了多长时间 ?
育红学校七年级学生步行到郊外旅行,1班的学生组成前队,步行的速度为4千米/时,2班的学生组成后队,速度为6千米/时,前队出发1小时后,后队出发, 同时后队派一名联络员骑自行车在两队之间不间断地 来回进行联络,他骑车的速度为12千米 /时。
请根据以上的事实提出问题并尝试回答。
问题2:后队追上前队时联络员行了多少路程?
问题3:联络员第一次追上前队时用了多长时间?
问题4:当后队追上前队时,他们已经行进了多少路程?
问题5:前队出发多长时间后,联络员第一次追上前队?
问题6:联络员追上前队后,用多长时间和后队相遇?
…….
智力擂台:
问题2:后队追上前队时联络员行了多少路程?
议一议:育红学校七年级学生步行到郊外旅行,1班的学生组成前队,步行的速度为4千米/时,2班的学生组成后队,速度为6千米/时,前队出发1小时后,后队出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时。
解:由问题1得后队追上前队用了2小时,因此联络员共行进了
12 × 2 = 24 (千米)
答:后队追上前队时联络员行了24千米。
问题1:后队追上前队用了多长时间 ?
解:设后队追上前队用了x小时,由题意得:
6x - 4x = 4
解得 x = 2
答:后队追上前队时用了2小时。
问题3:联络员第一次追上前队时用了多长时间?
解:设联络员第一次追上前队时用了x小时,
由题意列方程得
12x -4x = 4
解得 x = 0.5
答:联络员第一次追上前队时用了0.5小时。
议一议:育红学校七年级学生步行到郊外旅行,1班的学生组成前队,步行的速度为4千米/时,2班的学生组成后队,速度为6千米/时,前队出发1小时后,后队出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米 /时。
问题4:当后队追上前队时,他们已经行进了多少路程?
解得 x = 12
答:当后队追上前队时,他们已经行进12千米.
议一议:育红学校七年级学生步行到郊外旅行,1班的学生组成前队,步行的速度为4千米/时,2班的学生组成后队,速度为6千米/时,前队出发1小时后,后队出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时。
后队用的时间+1=前队用的时间
解:设当后队追上前队时,他们已经行进了X千米,
由题意得
方法二:
方法一:
后队速度×后队的时间
解:由问题1得后队追上前队用了2小时。(或前队行了3小时)
因此他们行进路程为6×2 =12千米。(或4×3=12千米)
1、一条船在两个码头间航行,顺水需4.5小时,逆水返回需5小时,水流速度是1千米/时,这两个码头相距多少千米?
思考题
数学教师寄语:只有想不到,没有做不到,努力永远都不会晚!
甲乙二人分别后,沿着铁轨反向而行。此时,一列火车匀速地向甲迎面驶来,列车在甲身旁开过,用了15秒;然后在乙身旁开过,用了17秒.已知两人步行速度都是3.6千米/时,这列火车有多长?它的速度是多少?
相遇
甲
追及
乙
车尾 车头
车身长
车尾 车头
车身长
图示
S人
S车
相遇点
甲乙二人分别后,沿着铁轨反向而行。此时,一列火车匀速地向甲迎面驶来,列车在甲身旁开过,用了15秒;然后在乙身旁开过,用了17秒.已知两人步行速度都是3.6千米/时,这列火车有多长?它的速度是多少?
千里之行,始于足下!
1、行程问题中的相等关系是:路程=速度×时间……
2、相遇问题常用的等量关系:
3、追击问题常用的等量关系:
S距=S快+S慢
S距=S快-S慢
4、(1)解应用题要会借助线段图来分析数量关系。
(2)学会文字语言、图形语言、符号语言的互相渗透,互相转换。
解:设t秒后甲、乙相遇,
据题意得 8t+6t =280
解,得 t=20
答:甲出发20秒与乙相遇.
例1:甲、乙两人相距280米,相向而行,甲从A地每
秒走8米,乙从B地每秒走6米,那么甲出发几秒
与乙相遇?
分析:等量关系:甲所用时间=乙所用时间;
甲路程+乙路程=甲乙相距路程.
线段图:
相遇问题
解:设快车x小时追上慢车,
据题意得: 85x - 5x=450
解,得 x=22.5
答:快车22.5小时追上慢车.
例2:甲、乙两站间的路程为450千米,一列慢车从甲站
开出,每小时行驶65千米,一列快车从乙站开出,
每小时行驶85千米.设两车同时开出,同向而行,
则快车几小时后追上慢车?
分析:等量关系:快车所用时间=慢车所用时间;
快车行驶路程=慢车行驶路程+相距路程.
线段图:
追及问题
例3:七年级一班列队以每小时6千米的速度去甲地.王明从
队尾以每小时10千米的速度赶到队伍的排头后又以同
样的速度返回排尾,一共用了7.5分钟,求队伍的长.
分析:追及问题:队尾追排头;
相遇问题:排头回队尾.
解:7.5分钟= 小时
设王明追上排头用了x小时,则返回用了( -x)小时,
据题意得 10 x-6 x =10( -x)+6( -x)
解,得 x=0.1
此时,10×0.1-6×0.1 =0.4(千米)=400(米)
答:队伍长为400米.
相遇和追及综合问题
在3点钟和4点种之间,钟表的时针和分针什么
时间重合?
2.甲、乙二人在400米环行跑道上散步,甲每分钟走110米,乙每分钟走90米,二人从同一地点出发,几分钟后二人第一次相遇?第二次?第n次呢?
数学教师寄语:努力永远都不会晚,成功的关键在于积累。
若冬子追赶红军部队至A地,此时部队在冬子前方210千米处,且于25千米/时的速度继续前行,于是冬子选择路边同方向的水路追赶。已知冬子所乘竹排的速度为55千米/时,你能帮冬子算出他需要几小时追上部队吗?
做一做
1.若小明每秒跑4米,那么他20秒能跑( )米.
80
S=v t
路程=速度 X 时间
做一做
2.已知小明家距离火车站2400米,他以4米/秒的速度骑车到达车站需要( )分。
t=s/v
时间=路程/速度
10
做一做
3.小明用2分钟绕学校操场跑了两圈(每圈300米),那么他的速度为( )米/秒.
速度=路程/时间
v=s/t
5
(1)相遇时,爸爸遇到小明用了多长时间?
(2)小明以同样的速度返回学校,能否迟到?
小明每天早上要在7:50分之前赶到距离家1000米的学校上学。一天7:40分她到校门口后,突然发现忘带了作业,连忙给爸爸打电话并以110米/分的速度向家跑回。与此同时爸爸也以140米/分的速度奔向学校,结果两人在途中相遇。
严谨认真
解:(1)设爸爸遇到小明用了 x 分,则
110 x+140 x=1000
(110+140)x=1000
x=4 答:爸爸遇到小明用4分钟。
(2)40+4x2=48<50 所以小明没迟到。
小明每天早上要在7:50之前赶到距离家1000米的学校上学。一天7:40分她到校门口后,突然发现忘带了作业,连忙给爸爸打电话并以110米/分的速度向家跑回。与此同时爸爸也以140米/分的速度奔向学校,结果两人在途中相遇。
(1)相遇时,爸爸遇到小明用了多长时间?
(2)小明以同样的速度返回学校,能否迟到?
相遇
(相向)
家
校
相遇
140 X 110X
1000米
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
小明每天早上要在7:50之前赶到距离家1000米的学校上学。小明以80米/分的速度出发,5分钟后,爸爸发现她忘了带语文书。又是爸爸立即以180米/分的速度去追小明,并在途中追上了她。
严谨认真
解:(1)设爸爸追上小明用了 x 分,则
180x–80 x = 80x5
(180–80)x = 80x5
x = 4 答:爸爸追上小明用4分钟。
(2)因为 180 x 4 = 720(米)
1000–720 = 280(米)
所以 追上小明时,距离学校还有280米。
小明每天早上要在7:50之前赶到距离家1000米的学校上学。小明以80米/分的速度出发,5分钟后,爸爸发现她忘了带语文书。于是爸爸立即以180米/分的速度去追小明,并在途中追上了她。
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
追击
(同向)
1000米
80x5 80x ?
180x
家
校
竹排的行程问题:
若冬子追赶红军部队至A地,此时部队在冬子前方210千米处,且于25千米/时的速度继续前行,于是冬子选择路边同方向的水路追赶。已知冬子所乘竹排的速度为55千米/时,你能帮冬子算出他需要几小时追上部队吗?
竹排的行程问题:
解:设冬子乘竹排需小时追上部队,
由题意得 55X-25X=210
30X=210
X=7
答:冬子追上部队需7小时。
1、行程问题中的相等关系是:路程=速度×时间.
2、相遇问题常用的等量关系:
3、追击问题常用的等量关系:
4、(1)解应用题要学会借助线段图来分析数量关系。
(2)学会文字语言、图形语言、符号语言的互相渗 透,互相转换。
S距=S快+S慢
S距=S快-S慢
即 S快=S距+S慢
1.小彬和小明跑步,小彬每秒跑4米,小明每秒跑6米。(1)若他们站在百米跑道的两端同时相向起跑,几秒后两人相遇?(2)若小明站在跑道的起点处,小彬站在他前面10米处,两人同时同向起跑,几秒后小明能追上小彬?
随堂练习
(2)设x秒后甲追上乙,根据题意得
6x-4x=10
解:(1)设x秒后两人相遇,根据题意得
6x+4x=100
只列方程不解
2.甲乙两地相距230千米,一辆卡车和一货客 车分别以50千米/时和40千米/时的速度从两地出发,相向而行,若卡车早出发1小时,则卡车再行几小时两车相遇?
解:设卡车行X小时两车相遇,
由题意得 50 + 50X+40X=230
50(1+X)+40X=230
90X=180
X=2
答:卡车行2小时两车相遇。
问题1:后队追上前队用了多长时间 ?
育红学校七年级学生步行到郊外旅行,1班的学生组成前队,步行的速度为4千米/时,2班的学生组成后队,速度为6千米/时,前队出发1小时后,后队出发, 同时后队派一名联络员骑自行车在两队之间不间断地 来回进行联络,他骑车的速度为12千米 /时。
请根据以上的事实提出问题并尝试回答。
问题2:后队追上前队时联络员行了多少路程?
问题3:联络员第一次追上前队时用了多长时间?
问题4:当后队追上前队时,他们已经行进了多少路程?
问题5:前队出发多长时间后,联络员第一次追上前队?
问题6:联络员追上前队后,用多长时间和后队相遇?
…….
智力擂台:
问题2:后队追上前队时联络员行了多少路程?
议一议:育红学校七年级学生步行到郊外旅行,1班的学生组成前队,步行的速度为4千米/时,2班的学生组成后队,速度为6千米/时,前队出发1小时后,后队出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时。
解:由问题1得后队追上前队用了2小时,因此联络员共行进了
12 × 2 = 24 (千米)
答:后队追上前队时联络员行了24千米。
问题1:后队追上前队用了多长时间 ?
解:设后队追上前队用了x小时,由题意得:
6x - 4x = 4
解得 x = 2
答:后队追上前队时用了2小时。
问题3:联络员第一次追上前队时用了多长时间?
解:设联络员第一次追上前队时用了x小时,
由题意列方程得
12x -4x = 4
解得 x = 0.5
答:联络员第一次追上前队时用了0.5小时。
议一议:育红学校七年级学生步行到郊外旅行,1班的学生组成前队,步行的速度为4千米/时,2班的学生组成后队,速度为6千米/时,前队出发1小时后,后队出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米 /时。
问题4:当后队追上前队时,他们已经行进了多少路程?
解得 x = 12
答:当后队追上前队时,他们已经行进12千米.
议一议:育红学校七年级学生步行到郊外旅行,1班的学生组成前队,步行的速度为4千米/时,2班的学生组成后队,速度为6千米/时,前队出发1小时后,后队出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时。
后队用的时间+1=前队用的时间
解:设当后队追上前队时,他们已经行进了X千米,
由题意得
方法二:
方法一:
后队速度×后队的时间
解:由问题1得后队追上前队用了2小时。(或前队行了3小时)
因此他们行进路程为6×2 =12千米。(或4×3=12千米)
1、一条船在两个码头间航行,顺水需4.5小时,逆水返回需5小时,水流速度是1千米/时,这两个码头相距多少千米?
思考题
数学教师寄语:只有想不到,没有做不到,努力永远都不会晚!
甲乙二人分别后,沿着铁轨反向而行。此时,一列火车匀速地向甲迎面驶来,列车在甲身旁开过,用了15秒;然后在乙身旁开过,用了17秒.已知两人步行速度都是3.6千米/时,这列火车有多长?它的速度是多少?
相遇
甲
追及
乙
车尾 车头
车身长
车尾 车头
车身长
图示
S人
S车
相遇点
甲乙二人分别后,沿着铁轨反向而行。此时,一列火车匀速地向甲迎面驶来,列车在甲身旁开过,用了15秒;然后在乙身旁开过,用了17秒.已知两人步行速度都是3.6千米/时,这列火车有多长?它的速度是多少?
千里之行,始于足下!
1、行程问题中的相等关系是:路程=速度×时间……
2、相遇问题常用的等量关系:
3、追击问题常用的等量关系:
S距=S快+S慢
S距=S快-S慢
4、(1)解应用题要会借助线段图来分析数量关系。
(2)学会文字语言、图形语言、符号语言的互相渗透,互相转换。
解:设t秒后甲、乙相遇,
据题意得 8t+6t =280
解,得 t=20
答:甲出发20秒与乙相遇.
例1:甲、乙两人相距280米,相向而行,甲从A地每
秒走8米,乙从B地每秒走6米,那么甲出发几秒
与乙相遇?
分析:等量关系:甲所用时间=乙所用时间;
甲路程+乙路程=甲乙相距路程.
线段图:
相遇问题
解:设快车x小时追上慢车,
据题意得: 85x - 5x=450
解,得 x=22.5
答:快车22.5小时追上慢车.
例2:甲、乙两站间的路程为450千米,一列慢车从甲站
开出,每小时行驶65千米,一列快车从乙站开出,
每小时行驶85千米.设两车同时开出,同向而行,
则快车几小时后追上慢车?
分析:等量关系:快车所用时间=慢车所用时间;
快车行驶路程=慢车行驶路程+相距路程.
线段图:
追及问题
例3:七年级一班列队以每小时6千米的速度去甲地.王明从
队尾以每小时10千米的速度赶到队伍的排头后又以同
样的速度返回排尾,一共用了7.5分钟,求队伍的长.
分析:追及问题:队尾追排头;
相遇问题:排头回队尾.
解:7.5分钟= 小时
设王明追上排头用了x小时,则返回用了( -x)小时,
据题意得 10 x-6 x =10( -x)+6( -x)
解,得 x=0.1
此时,10×0.1-6×0.1 =0.4(千米)=400(米)
答:队伍长为400米.
相遇和追及综合问题
在3点钟和4点种之间,钟表的时针和分针什么
时间重合?
2.甲、乙二人在400米环行跑道上散步,甲每分钟走110米,乙每分钟走90米,二人从同一地点出发,几分钟后二人第一次相遇?第二次?第n次呢?
数学教师寄语:努力永远都不会晚,成功的关键在于积累。
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
