华师大版九上:23.3.4 相似三角形的应用 教案
文档属性
| 名称 | 华师大版九上:23.3.4 相似三角形的应用 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 661.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-06 12:14:02 | ||
图片预览


文档简介
23.3 相似三角形
相似三角形的应用
&.教学目标:
1、掌握利用三角形相似测量高度或宽度的方法。
2、通过自己设计方案测量高度体会相似三角形在解决实际问题中的广泛应用。
3、利用相似解决实际问题,进一步提高学生应用数学知识的能力。
&.教学重点、难点:
重点:能构建相似三角形解决实际问题。
难点:把实际问题抽象为数学问题,利用相似三角形解决问题。
&.教学过程:
一、情境导入
1、回顾:判定两个三角形相似的方法有几种?分别是哪几种?相似三角形有哪些性质?
2、问题:古埃及所有金字塔中最大一座,是第四王朝法老胡夫的金字塔,这座金字塔原高米,经过几千年的风吹雨打,顶端被风化吹蚀了将近米。巴黎埃菲尔铁塔完成之前,它一直是世界上最到的建筑物。这座金字塔的底面呈正方形,边长约为多米,你知道金字塔的高度是如何利用相似知识测量出来的吗?(引出课题)
二、探究新知
§.探究利用相似三角形解决实际问题
问题1:如图,古代一位数学家想出了一种测量金字塔高度的方法:为了测量金字塔的高度,先竖一根已知长度的木棒,比较棒子的影长金字塔的影长,即可近似算出金字塔的高度.如果,,,求金字塔的高度.
解:由于太阳光是平行光线
∴
∵
∴∽(两个对应相等,两个三角形相似)
∴
∴(米)
即该金字塔高为米。
问题2:如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点,再在河的这一边选定点和,使,然后,再选点,使,用视线确定和的交点.此时如果测得米,米,米,求两岸间的大致距离.
解:∵,
∴∽(两个对应相等,两个三角形相似)
∴
解得(米).
答:两岸间的大致距离为米。
通过以上两个例题,请同学们思考下列问题:
(1)利用相似三角形解决实际问题的关键是什么?
(2)相似三角形常用来解决哪几类问题?
归纳:
(1)利用相似三角形解决实际问题的关键是把实际问题通过建立数学模型转化为数学问题,根据题意构造相似三角形,解题过程中首先要画出图形。
(2)相似三角形常用来解决测量高度或估计宽度的问题.①利用太阳光下的影子测量物体的高度直接运用了三角形相似,根据太阳光线是平行光线,所以同一时刻光线与地面的夹角都相等。又物体的高和标杆都与地面垂直,所以由标杆与其影子及光线组成的三角形、被测物体的高与影子及光线组成的三角形相似,而影子和标杆的高均可测量,因此可利用相似三角形对应边成比例求出被测物体的高度。②利用相似三角形估算不可直接测量的宽度的问题,实质上就是构造直角三角形,利用对应边成比例求出估算的宽度。
三、讲解例题,巩固新知
§.例1、如图,用一桶农药给果树防虫,桶高,桶内有一斜放的木棒,一端在桶底,另一端恰好在桶盖口处,木棒总长为,下面浸有农药的部分长,你能求出桶内药液的高度吗?
解析:因为液面与桶底是平行的,所以可以得到∽,根据题中其他条件可求得桶内药液的高度。
解:由题意可求得桶∽
∵,
∴
设桶内药液的高度为
∴
解得:
答:桶内药液的高度为.
§.例2、阅读并解答下面问题:
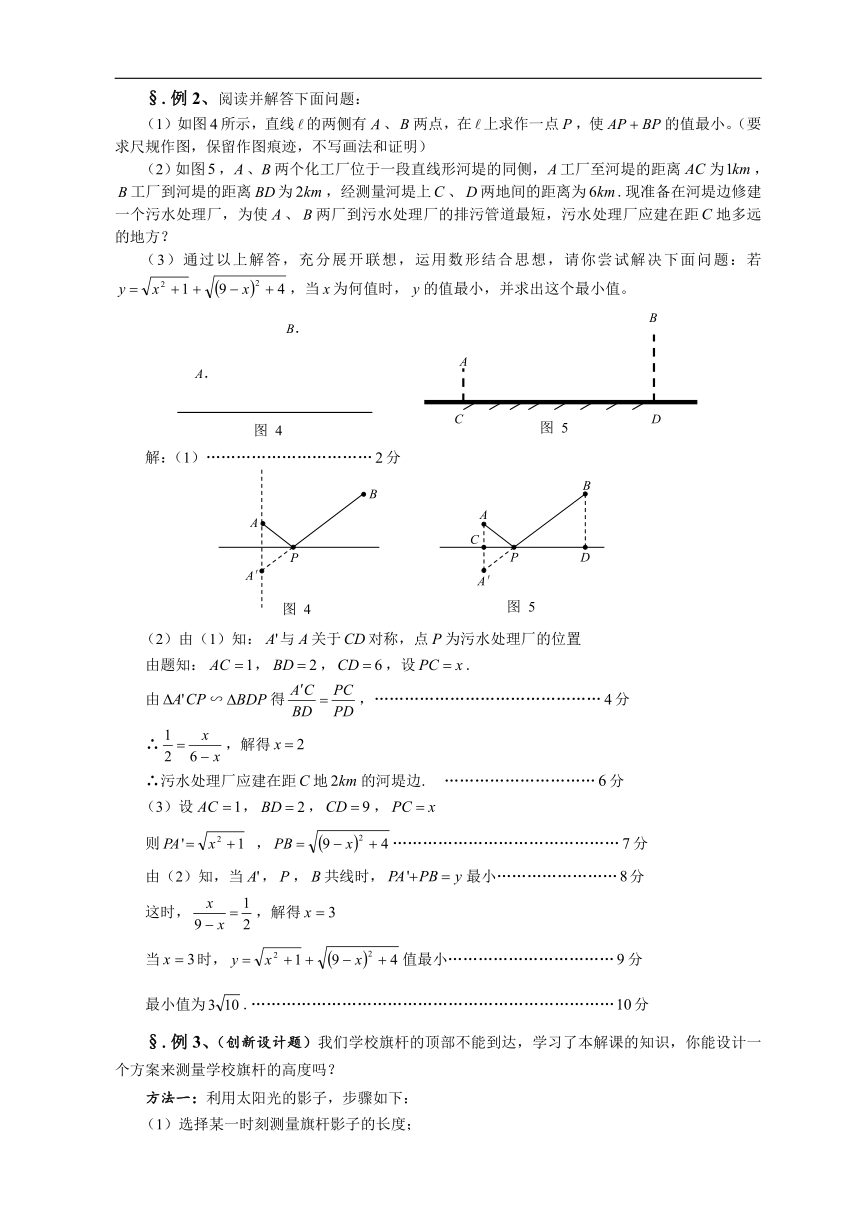
(1)如图所示,直线的两侧有、两点,在上求作一点,使的值最小。(要求尺规作图,保留作图痕迹,不写画法和证明)
(2)如图,、两个化工厂位于一段直线形河堤的同侧,工厂至河堤的距离为,工厂到河堤的距离为,经测量河堤上、两地间的距离为.现准备在河堤边修建一个污水处理厂,为使、两厂到污水处理厂的排污管道最短,污水处理厂应建在距地多远的地方?
(3)通过以上解答,充分展开联想,运用数形结合思想,请你尝试解决下面问题:若,当为何值时,的值最小,并求出这个最小值。
解:(1)……………………………分
(2)由(1)知:与关于对称,点为污水处理厂的位置
由题知:,,,设.
由∽得,………………………………………分
∴,解得
∴污水处理厂应建在距地的河堤边. …………………………分
(3)设,,,
则 ,………………………………………分
由(2)知,当,,共线时,最小……………………分
这时,,解得
当时,值最小……………………………分
最小值为.………………………………………………………………分
§.例3、(创新设计题)我们学校旗杆的顶部不能到达,学习了本解课的知识,你能设计一个方案来测量学校旗杆的高度吗?
方法一:利用太阳光的影子,步骤如下:
(1)选择某一时刻测量旗杆影子的长度;
(2)同一时刻在太阳光下立一个标杆,测量标杆和标杆形成影子的长度;
(3)利用三角形相似来计算旗杆的长度。
方法二:利用标杆。
当没有太阳光时,可采用如下方法:在地面上竖直立两根标杆,观测者与标杆的顶端、旗杆的顶端共线,利用两次三角形相似计算旗杆的高度。
方法三:利用平面镜也可测量,过程略。
§.例4、 如图,已知:、是的边、上的点,且.
求证:.
证明:∵,
∴∽(两角对应相等,两个三角形相似).
∴,
∴
§.例5、如图,中,、,,点(与点、不重合)在边上,交于点.
(1)当的面积与四边形的面积相等时,求的长;
(2)当的周长与四边形的周长相等时,求的长;
(3)试问在上是否存在点,使得为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出的长。
解:(1)∵的面积与四边形的面积相等。
∴ ………………………………………分
又∵
∴∽ …………………………………………分
∴且
∴…………………………………………………分
(2)设的长为
∵∽
∴
∴…………………………………………………分
由的面积与四边形的周长相等,得:
………………分
解得
∴的长为……………………………………………分
(3)为等腰直角三角形,有两种情况:
①如图(),假设,.
由,,,得
∴斜边上高
设,由∽,得
,即
解得,即
当,时,同理可得…………分
②如图(),假设,时,点到的距离为.
设,由∽,得:,即
解得,即
综上所述,在上存在点,使为等腰直角三角形
此时或…………………………… …分
四、巩固练习
教材 练习
五、课堂小结
通过本节课的学习,要求同学们
1、理解相似三角形的知识应用非常广泛,特别是在测量不可到达的高度或宽度问题中时常用到。
2、解决实际问题的关键是将实际问题建立模型转化为数学问题,构造相似三角形利用对应边成比例求出高度和宽度。
六、课外作业
1、教材 习题
2、补充题:
.高为的旗杆在水平地面上的影子长,此时测得附近一个建筑物的影子长,求该建筑物的高度。
.如图,在离某建筑物处有一棵树,在某一时刻,长的竹竿竖直地面,影子为,此时,树的影子照射地面,还有一部分在建筑物的墙上,墙上的影子为,那么这棵树高约是多少米?
提示:树可分为两部分,一部分影子落在地面上,一部分影子落在墙上,根据太阳光线是平行光线,落在墙上的部分高度等于影子的长度,设此影子的长度,影子落在地面的部分可根据物高与影子成正比,可得,解得,故这棵树高约为.
.如图,点是四边形的对角线上一点,且.
(1)求证:;
(2)根据图形特点,猜想可能等于哪两条线段的比.(注:只需写出图中已知有线段的一组比即可)并证明你的猜想。
提示:(1)证明∽即可;(2)(或).
.如图,已知中,,,试说明:.
.在()的边上取一点,在边上取一点,使,直线和的延长线交于点,求证:.
提示:经过点作的平行线。
.过的顶点任作一直线,与边及中线分别交于点和,求证:
提示:经过点作交于点.
.中有正方形,点、分别在、上,在斜边上,求证:.
.如图,,求证:.
提示:过点作交于.
相似三角形的应用
&.教学目标:
1、掌握利用三角形相似测量高度或宽度的方法。
2、通过自己设计方案测量高度体会相似三角形在解决实际问题中的广泛应用。
3、利用相似解决实际问题,进一步提高学生应用数学知识的能力。
&.教学重点、难点:
重点:能构建相似三角形解决实际问题。
难点:把实际问题抽象为数学问题,利用相似三角形解决问题。
&.教学过程:
一、情境导入
1、回顾:判定两个三角形相似的方法有几种?分别是哪几种?相似三角形有哪些性质?
2、问题:古埃及所有金字塔中最大一座,是第四王朝法老胡夫的金字塔,这座金字塔原高米,经过几千年的风吹雨打,顶端被风化吹蚀了将近米。巴黎埃菲尔铁塔完成之前,它一直是世界上最到的建筑物。这座金字塔的底面呈正方形,边长约为多米,你知道金字塔的高度是如何利用相似知识测量出来的吗?(引出课题)
二、探究新知
§.探究利用相似三角形解决实际问题
问题1:如图,古代一位数学家想出了一种测量金字塔高度的方法:为了测量金字塔的高度,先竖一根已知长度的木棒,比较棒子的影长金字塔的影长,即可近似算出金字塔的高度.如果,,,求金字塔的高度.
解:由于太阳光是平行光线
∴
∵
∴∽(两个对应相等,两个三角形相似)
∴
∴(米)
即该金字塔高为米。
问题2:如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点,再在河的这一边选定点和,使,然后,再选点,使,用视线确定和的交点.此时如果测得米,米,米,求两岸间的大致距离.
解:∵,
∴∽(两个对应相等,两个三角形相似)
∴
解得(米).
答:两岸间的大致距离为米。
通过以上两个例题,请同学们思考下列问题:
(1)利用相似三角形解决实际问题的关键是什么?
(2)相似三角形常用来解决哪几类问题?
归纳:
(1)利用相似三角形解决实际问题的关键是把实际问题通过建立数学模型转化为数学问题,根据题意构造相似三角形,解题过程中首先要画出图形。
(2)相似三角形常用来解决测量高度或估计宽度的问题.①利用太阳光下的影子测量物体的高度直接运用了三角形相似,根据太阳光线是平行光线,所以同一时刻光线与地面的夹角都相等。又物体的高和标杆都与地面垂直,所以由标杆与其影子及光线组成的三角形、被测物体的高与影子及光线组成的三角形相似,而影子和标杆的高均可测量,因此可利用相似三角形对应边成比例求出被测物体的高度。②利用相似三角形估算不可直接测量的宽度的问题,实质上就是构造直角三角形,利用对应边成比例求出估算的宽度。
三、讲解例题,巩固新知
§.例1、如图,用一桶农药给果树防虫,桶高,桶内有一斜放的木棒,一端在桶底,另一端恰好在桶盖口处,木棒总长为,下面浸有农药的部分长,你能求出桶内药液的高度吗?
解析:因为液面与桶底是平行的,所以可以得到∽,根据题中其他条件可求得桶内药液的高度。
解:由题意可求得桶∽
∵,
∴
设桶内药液的高度为
∴
解得:
答:桶内药液的高度为.
§.例2、阅读并解答下面问题:
(1)如图所示,直线的两侧有、两点,在上求作一点,使的值最小。(要求尺规作图,保留作图痕迹,不写画法和证明)
(2)如图,、两个化工厂位于一段直线形河堤的同侧,工厂至河堤的距离为,工厂到河堤的距离为,经测量河堤上、两地间的距离为.现准备在河堤边修建一个污水处理厂,为使、两厂到污水处理厂的排污管道最短,污水处理厂应建在距地多远的地方?
(3)通过以上解答,充分展开联想,运用数形结合思想,请你尝试解决下面问题:若,当为何值时,的值最小,并求出这个最小值。
解:(1)……………………………分
(2)由(1)知:与关于对称,点为污水处理厂的位置
由题知:,,,设.
由∽得,………………………………………分
∴,解得
∴污水处理厂应建在距地的河堤边. …………………………分
(3)设,,,
则 ,………………………………………分
由(2)知,当,,共线时,最小……………………分
这时,,解得
当时,值最小……………………………分
最小值为.………………………………………………………………分
§.例3、(创新设计题)我们学校旗杆的顶部不能到达,学习了本解课的知识,你能设计一个方案来测量学校旗杆的高度吗?
方法一:利用太阳光的影子,步骤如下:
(1)选择某一时刻测量旗杆影子的长度;
(2)同一时刻在太阳光下立一个标杆,测量标杆和标杆形成影子的长度;
(3)利用三角形相似来计算旗杆的长度。
方法二:利用标杆。
当没有太阳光时,可采用如下方法:在地面上竖直立两根标杆,观测者与标杆的顶端、旗杆的顶端共线,利用两次三角形相似计算旗杆的高度。
方法三:利用平面镜也可测量,过程略。
§.例4、 如图,已知:、是的边、上的点,且.
求证:.
证明:∵,
∴∽(两角对应相等,两个三角形相似).
∴,
∴
§.例5、如图,中,、,,点(与点、不重合)在边上,交于点.
(1)当的面积与四边形的面积相等时,求的长;
(2)当的周长与四边形的周长相等时,求的长;
(3)试问在上是否存在点,使得为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出的长。
解:(1)∵的面积与四边形的面积相等。
∴ ………………………………………分
又∵
∴∽ …………………………………………分
∴且
∴…………………………………………………分
(2)设的长为
∵∽
∴
∴…………………………………………………分
由的面积与四边形的周长相等,得:
………………分
解得
∴的长为……………………………………………分
(3)为等腰直角三角形,有两种情况:
①如图(),假设,.
由,,,得
∴斜边上高
设,由∽,得
,即
解得,即
当,时,同理可得…………分
②如图(),假设,时,点到的距离为.
设,由∽,得:,即
解得,即
综上所述,在上存在点,使为等腰直角三角形
此时或…………………………… …分
四、巩固练习
教材 练习
五、课堂小结
通过本节课的学习,要求同学们
1、理解相似三角形的知识应用非常广泛,特别是在测量不可到达的高度或宽度问题中时常用到。
2、解决实际问题的关键是将实际问题建立模型转化为数学问题,构造相似三角形利用对应边成比例求出高度和宽度。
六、课外作业
1、教材 习题
2、补充题:
.高为的旗杆在水平地面上的影子长,此时测得附近一个建筑物的影子长,求该建筑物的高度。
.如图,在离某建筑物处有一棵树,在某一时刻,长的竹竿竖直地面,影子为,此时,树的影子照射地面,还有一部分在建筑物的墙上,墙上的影子为,那么这棵树高约是多少米?
提示:树可分为两部分,一部分影子落在地面上,一部分影子落在墙上,根据太阳光线是平行光线,落在墙上的部分高度等于影子的长度,设此影子的长度,影子落在地面的部分可根据物高与影子成正比,可得,解得,故这棵树高约为.
.如图,点是四边形的对角线上一点,且.
(1)求证:;
(2)根据图形特点,猜想可能等于哪两条线段的比.(注:只需写出图中已知有线段的一组比即可)并证明你的猜想。
提示:(1)证明∽即可;(2)(或).
.如图,已知中,,,试说明:.
.在()的边上取一点,在边上取一点,使,直线和的延长线交于点,求证:.
提示:经过点作的平行线。
.过的顶点任作一直线,与边及中线分别交于点和,求证:
提示:经过点作交于点.
.中有正方形,点、分别在、上,在斜边上,求证:.
.如图,,求证:.
提示:过点作交于.
