华东师大版八年级数学上册第13章全等三角形检测题(word版含答案)
文档属性
| 名称 | 华东师大版八年级数学上册第13章全等三角形检测题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 290.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 20:12:24 | ||
图片预览


文档简介
第13章检测题
时间:120分钟 满分:120分
一、选择题(每小题3分,共30分)
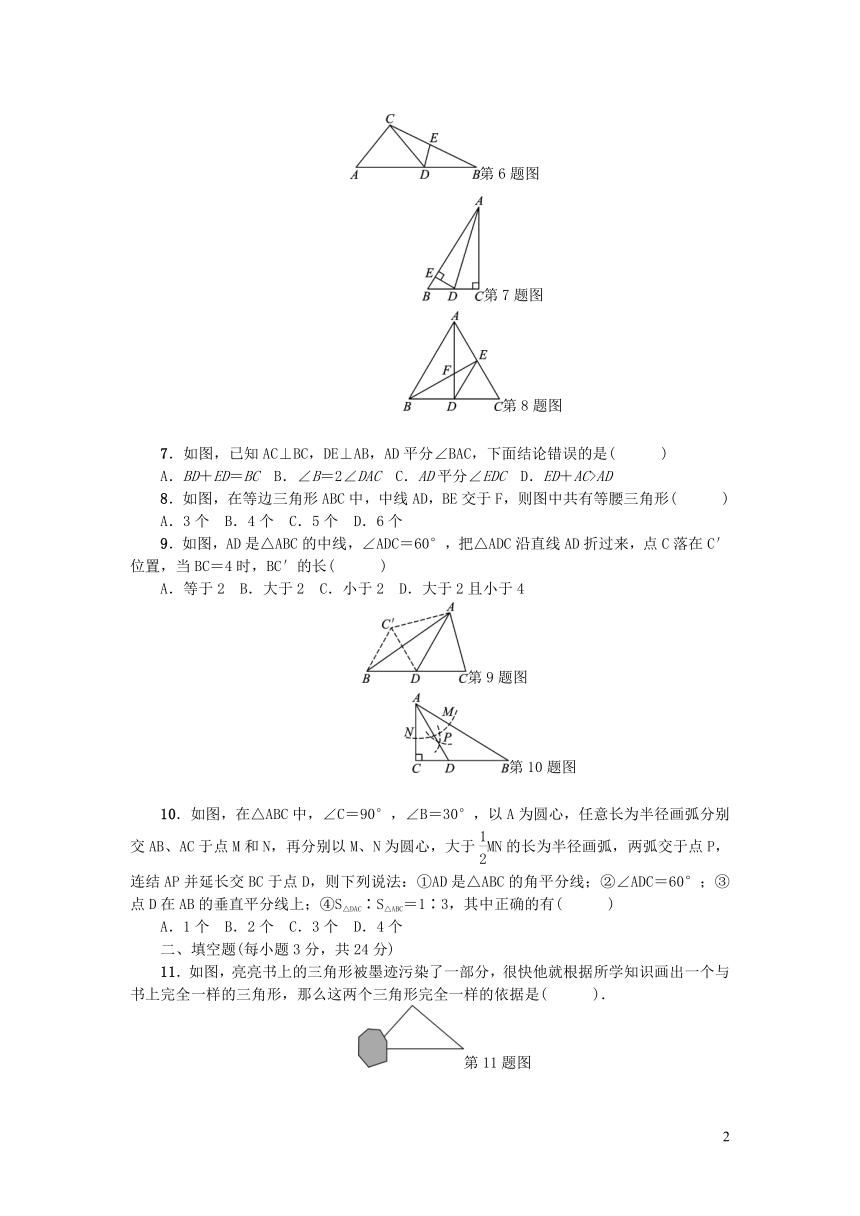
1.下列命题的逆命题中是假命题的是(
)
A.有一个内角等于60°的等腰三角形是等边三角形
B.对顶角相等
C.线段垂直平分线上的点到这条线段两个端点的距离相等
D.角的内部到角的两边距离相等的点在这个角的平分线上
2.如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是(
)
A.AB=DE
B.AC=DF
C.∠A=∠D
D.BF=EC
第2题图
第3题图
第5题图
3.如图,∠1=∠2,∠3=∠4,则下面结论中错误的是(
)
A.△ADC≌△BCD
B.△ABD≌△BAC
C.△ABO≌△COD
D.△AOD≌△BOC
4.用尺规作图:“已知底边和底边上的高,求作等腰三角形”,有下列作法:①作线段BC=a;②作线段BC的垂直平分线m,交BC于点D;③在直线m上截取DA=h,连结AB,AC.这样作法的根据是(
)
A.线段垂直平分线上的点到线段两个端点的距离相等
B.角平分线上的点到这个角两边的距离相等
C.等角对等边
D.等腰三角形的对称性
5.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19
cm,△ABD的周长为13
cm,则AE的长为(
)
A.3
cm
B.6
cm
C.12
cm
D.16
cm
6.如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为(
)
A.50°
B.51°
C.51.5°
D.52.5°
第6题图
第7题图
第8题图
7.如图,已知AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是(
)
A.BD+ED=BC
B.∠B=2∠DAC
C.AD平分∠EDC
D.ED+AC>AD
8.如图,在等边三角形ABC中,中线AD,BE交于F,则图中共有等腰三角形(
)
A.3个
B.4个
C.5个
D.6个
9.如图,AD是△ABC的中线,∠ADC=60°,把△ADC沿直线AD折过来,点C落在C′位置,当BC=4时,BC′的长(
)
A.等于2
B.大于2
C.小于2
D.大于2且小于4
第9题图
第10题图
10.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法:①AD是△ABC的角平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC∶S△ABC=1∶3,其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题3分,共24分)
11.如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是(
).
第11题图
第13题图
第14题图
第15题图
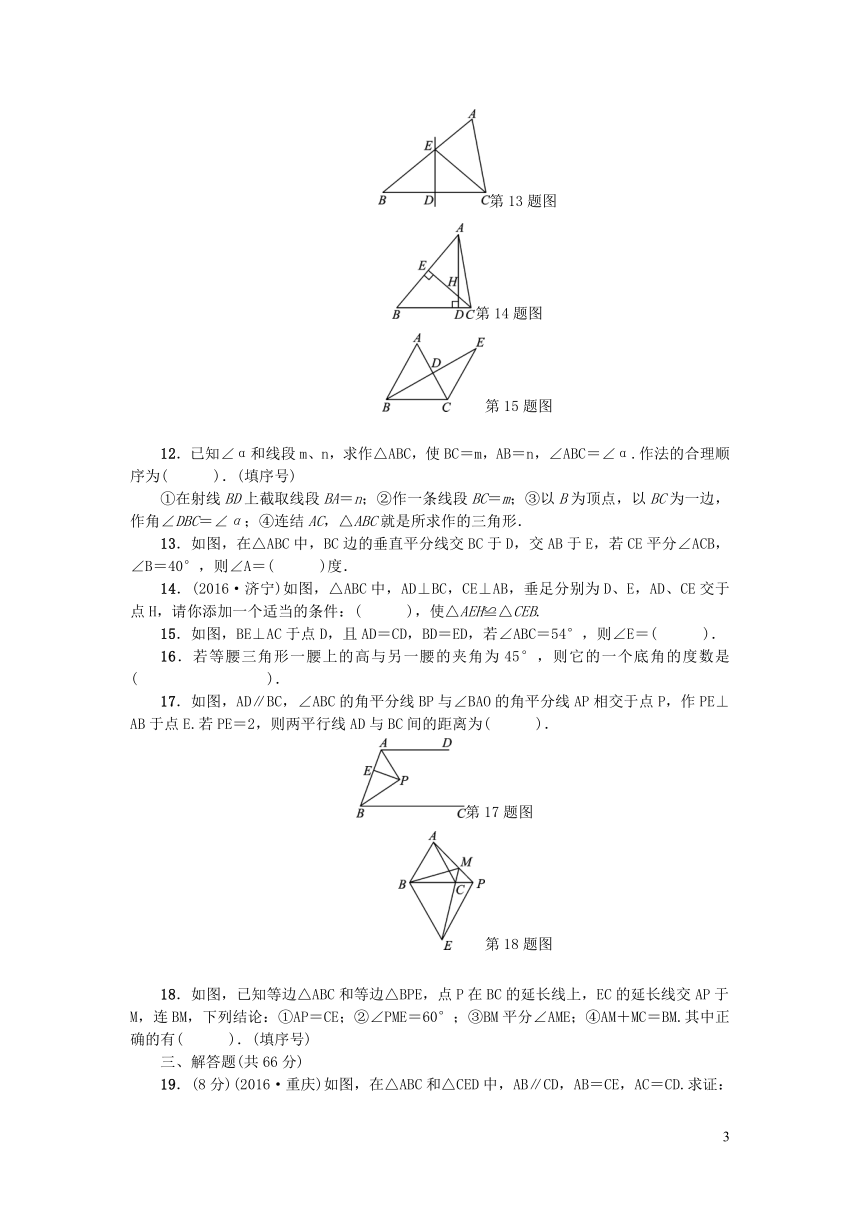
12.已知∠α和线段m、n,求作△ABC,使BC=m,AB=n,∠ABC=∠α.作法的合理顺序为(
).(填序号)
①在射线BD上截取线段BA=n;②作一条线段BC=m;③以B为顶点,以BC为一边,作角∠DBC=∠α;④连结AC,△ABC就是所求作的三角形.
13.如图,在△ABC中,BC边的垂直平分线交BC于D,交AB于E,若CE平分∠ACB,∠B=40°,则∠A=(
)度.
14.(2016·济宁)如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:(
),使△AEH≌△CEB.
15.如图,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=(
).
16.若等腰三角形一腰上的高与另一腰的夹角为45°,则它的一个底角的度数是(
).
17.如图,AD∥BC,∠ABC的角平分线BP与∠BAO的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为(
).
第17题图
第18题图
18.如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM,下列结论:①AP=CE;②∠PME=60°;③BM平分∠AME;④AM+MC=BM.其中正确的有(
).(填序号)
三、解答题(共66分)
19.(8分)(2016·重庆)如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.
20.(9分)如图,在△ABC中,点D是∠BAC的角平分线上一点,BD⊥AD于点D,过点D作DE∥AC交AB于点E.试判断△BED的形状,并说明理由.
21.(8分)有公路l1同侧、l2异侧的两个城镇A,B,如图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点.(保留作图痕迹,不要求写出作法)
.
22.(9分)如图①,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图②,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其他条件不变.求证:△AEF≌△BCF.
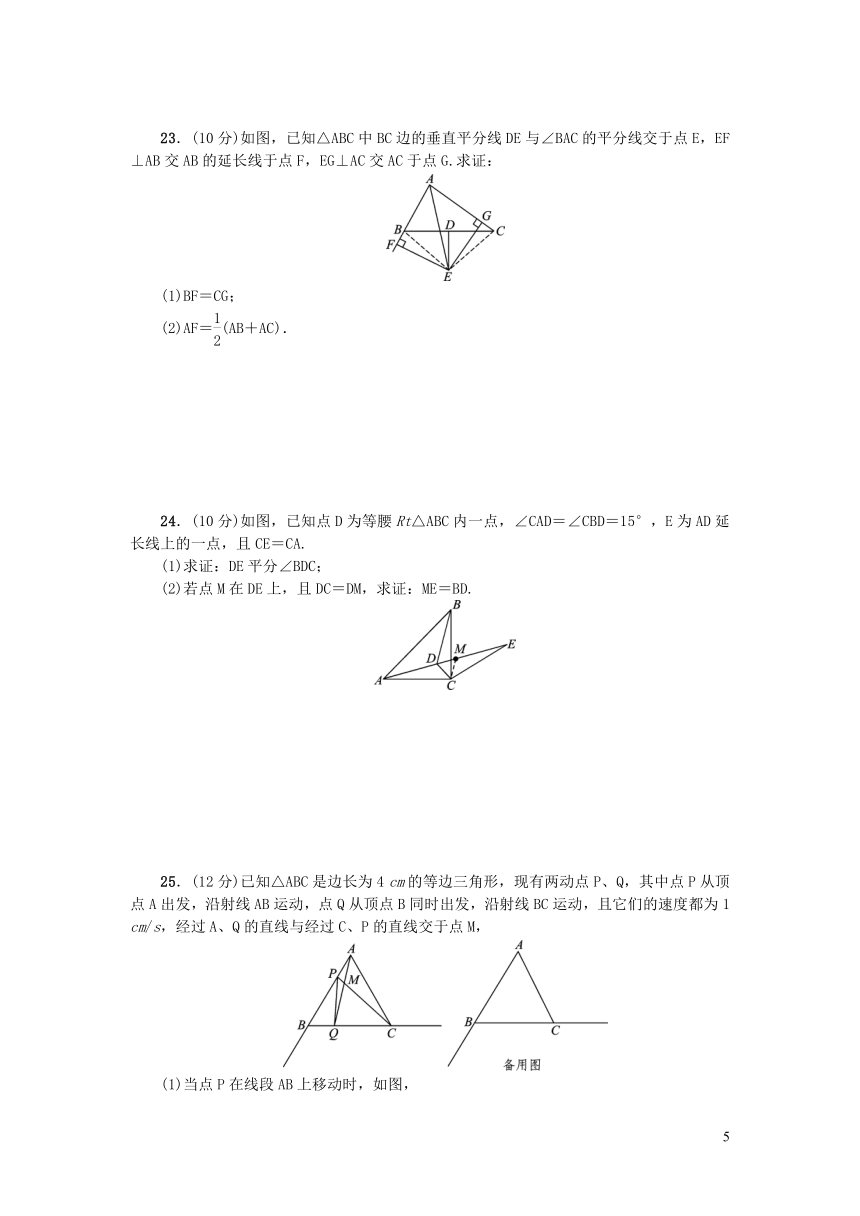
23.(10分)如图,已知△ABC中BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交AC于点G.求证:
(1)BF=CG;
(2)AF=(AB+AC).
24.(10分)如图,已知点D为等腰Rt△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
25.(12分)已知△ABC是边长为4
cm的等边三角形,现有两动点P、Q,其中点P从顶点A出发,沿射线AB运动,点Q从顶点B同时出发,沿射线BC运动,且它们的速度都为1
cm/s,经过A、Q的直线与经过C、P的直线交于点M,
(1)当点P在线段AB上移动时,如图,
①试判定线段AP与BQ的数量关系;(直接写出结果)
②试说明△ABQ≌△CAP;
(2)试探索:在P、Q运动的过程中,∠CMQ的大小变化吗?若变化,请说明理由;若不变,求出它的度数.
第13章检测题(答案版)
时间:120分钟 满分:120分
一、选择题(每小题3分,共30分)
1.下列命题的逆命题中是假命题的是(
B
)
A.有一个内角等于60°的等腰三角形是等边三角形
B.对顶角相等
C.线段垂直平分线上的点到这条线段两个端点的距离相等
D.角的内部到角的两边距离相等的点在这个角的平分线上
2.如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是(
C
)
A.AB=DE
B.AC=DF
C.∠A=∠D
D.BF=EC
第2题图
第3题图
第5题图
3.如图,∠1=∠2,∠3=∠4,则下面结论中错误的是(
C
)
A.△ADC≌△BCD
B.△ABD≌△BAC
C.△ABO≌△COD
D.△AOD≌△BOC
4.用尺规作图:“已知底边和底边上的高,求作等腰三角形”,有下列作法:①作线段BC=a;②作线段BC的垂直平分线m,交BC于点D;③在直线m上截取DA=h,连结AB,AC.这样作法的根据是(
A
)
A.线段垂直平分线上的点到线段两个端点的距离相等
B.角平分线上的点到这个角两边的距离相等
C.等角对等边
D.等腰三角形的对称性
5.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19
cm,△ABD的周长为13
cm,则AE的长为(
A
)
A.3
cm
B.6
cm
C.12
cm
D.16
cm
6.如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为(
D
)
A.50°
B.51°
C.51.5°
D.52.5°
第6题图
第7题图
第8题图
7.如图,已知AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是(
B
)
A.BD+ED=BC
B.∠B=2∠DAC
C.AD平分∠EDC
D.ED+AC>AD
8.如图,在等边三角形ABC中,中线AD,BE交于F,则图中共有等腰三角形(
D
)
A.3个
B.4个
C.5个
D.6个
9.如图,AD是△ABC的中线,∠ADC=60°,把△ADC沿直线AD折过来,点C落在C′位置,当BC=4时,BC′的长(
A
)
A.等于2
B.大于2
C.小于2
D.大于2且小于4
第9题图
第10题图
10.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法:①AD是△ABC的角平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC∶S△ABC=1∶3,其中正确的有(
D
)
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题3分,共24分)
11.如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是__A.S.A.__.
第11题图
第13题图
第14题图
第15题图
12.已知∠α和线段m、n,求作△ABC,使BC=m,AB=n,∠ABC=∠α.作法的合理顺序为__②③①④__.(填序号)
①在射线BD上截取线段BA=n;②作一条线段BC=m;③以B为顶点,以BC为一边,作角∠DBC=∠α;④连结AC,△ABC就是所求作的三角形.
13.如图,在△ABC中,BC边的垂直平分线交BC于D,交AB于E,若CE平分∠ACB,∠B=40°,则∠A=__60__度.
14.(2016·济宁)如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:__AH=CB或EH=EB或AE=CE(只要符合要求即可)__,使△AEH≌△CEB.
15.如图,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=__27°__.
16.若等腰三角形一腰上的高与另一腰的夹角为45°,则它的一个底角的度数是__22.5°或67.5°__.
17.如图,AD∥BC,∠ABC的角平分线BP与∠BAO的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为__4__.
第17题图
第18题图
18.如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM,下列结论:①AP=CE;②∠PME=60°;③BM平分∠AME;④AM+MC=BM.其中正确的有__①②③④__.(填序号)
三、解答题(共66分)
19.(8分)(2016·重庆)如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.
证明:∵AB∥CD,∴∠BAC=∠ECD.在△ABC和△CED中,,∴△ABC≌△CED(S.A.S.)∴∠B=∠E.
20.(9分)如图,在△ABC中,点D是∠BAC的角平分线上一点,BD⊥AD于点D,过点D作DE∥AC交AB于点E.试判断△BED的形状,并说明理由.
解:△BED是等腰三角形.理由:∵DE∥AC,∴∠CAD=∠EDA.∵∠CAD=∠DAE,∴∠EDA=∠EAD.∵∠EAD+∠EBD=90°,∠EDA+∠EDB=90°,∴∠EBD=∠EDB,∴EB=ED,∴△BED是等腰三角形.
21.(8分)有公路l1同侧、l2异侧的两个城镇A,B,如图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点.(保留作图痕迹,不要求写出作法)
解:如图.
点C1,C2就是符合条件的点.
22.(9分)如图①,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图②,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其他条件不变.求证:△AEF≌△BCF.
证明:(1)∵AB=AC,D是BC的中点,∴∠BAE=∠EAC.在△ABE和△ACE中,
∴△ABE≌△ACE(S.A.S.),∴BE=CE.
(2)∵∠BAC=45°,BF⊥AF,∴△ABF为等腰直角三角形,∴AF=BF.∵AB=AC,点D是BC的中点,∴AD⊥BC,∴∠EAF+∠C=90°.∵BF⊥AC,∴∠CBF+∠C=90°.∴∠EAF=∠CBF.
在△AEF和△BCF中,∴△AEF≌△BCF(A.S.A.)
23.(10分)如图,已知△ABC中BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交AC于点G.求证:
(1)BF=CG;
(2)AF=(AB+AC).
证明:(1)连结BE,CE.∵AE平分∠BAC,EF⊥AB,EG⊥AC,∴EF=EG,∵DE垂直平分BC,∴EB=EC.在Rt△EFB和Rt△EGC中,∴Rt△EFB≌Rt△EGC(H.L.),∴BF=CG.
(2)∵BF=CG,∴AB+AC=AB+BF+AG=AF+AG.又易证Rt△AEF≌Rt△AEG(H.L.),∴AF=AG,∴AF=(AB+AC).
24.(10分)如图,已知点D为等腰Rt△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
解:(1)∵△ABC为等腰直角三角形,∴AC=BC,∠CAB=∠CBA=45°.又∠CAD=∠CBD=15°,∴∠DAB=∠DBA=30°,∴DA=DB.又CD=CD,∴△ACD≌△BCD(S.S.S.),∴∠ACD=∠BCD=∠ACB=45°.∵∠CDE=∠CAD+∠ACD=15°+45°=60°,∠BDE=∠DAB+∠DBA=30°+30°=60°,∴∠CDE=∠BDE,即DE平分∠BDC.
(2)连结CM,由(1)知,∠CDE=60°,又DC=DM,∴△CDM是等边三角形,∴CM=CD,∠CMD=60°.∵CE=CA,∴∠E=∠CAD=15°,∴∠ECM=∠CMD-∠E=60°-15°=45°,∴∠ECM=∠BCD=45°.又CE=CA=CB,∴△BCD≌△ECM(S.A.S.),∴EM=BD.
25.(12分)已知△ABC是边长为4
cm的等边三角形,现有两动点P、Q,其中点P从顶点A出发,沿射线AB运动,点Q从顶点B同时出发,沿射线BC运动,且它们的速度都为1
cm/s,经过A、Q的直线与经过C、P的直线交于点M,
(1)当点P在线段AB上移动时,如图,
①试判定线段AP与BQ的数量关系;(直接写出结果)
②试说明△ABQ≌△CAP;
(2)试探索:在P、Q运动的过程中,∠CMQ的大小变化吗?若变化,请说明理由;若不变,求出它的度数.
解:(1)①AP=BQ.②∵等边三角形ABC中,AB=AC,∠ABC=∠CAP=60°,又由条件得AP=BQ,∴△ABQ≌△CAP(S.A.S.).
(2)①当点P在线段AB上移动时,这时,点Q在线段BC上移动.如图①,∠CMQ的大小不变.
∵△ABQ≌△CAP,∴∠BAQ=∠ACP,
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°.
②当点P在线段AB的延长线上移动时,点Q在线段BC的延长线上移动.如图②,∠CMQ的大小也不变.求法同①,此时∠CMQ=120°.
1
时间:120分钟 满分:120分
一、选择题(每小题3分,共30分)
1.下列命题的逆命题中是假命题的是(
)
A.有一个内角等于60°的等腰三角形是等边三角形
B.对顶角相等
C.线段垂直平分线上的点到这条线段两个端点的距离相等
D.角的内部到角的两边距离相等的点在这个角的平分线上
2.如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是(
)
A.AB=DE
B.AC=DF
C.∠A=∠D
D.BF=EC
第2题图
第3题图
第5题图
3.如图,∠1=∠2,∠3=∠4,则下面结论中错误的是(
)
A.△ADC≌△BCD
B.△ABD≌△BAC
C.△ABO≌△COD
D.△AOD≌△BOC
4.用尺规作图:“已知底边和底边上的高,求作等腰三角形”,有下列作法:①作线段BC=a;②作线段BC的垂直平分线m,交BC于点D;③在直线m上截取DA=h,连结AB,AC.这样作法的根据是(
)
A.线段垂直平分线上的点到线段两个端点的距离相等
B.角平分线上的点到这个角两边的距离相等
C.等角对等边
D.等腰三角形的对称性
5.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19
cm,△ABD的周长为13
cm,则AE的长为(
)
A.3
cm
B.6
cm
C.12
cm
D.16
cm
6.如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为(
)
A.50°
B.51°
C.51.5°
D.52.5°
第6题图
第7题图
第8题图
7.如图,已知AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是(
)
A.BD+ED=BC
B.∠B=2∠DAC
C.AD平分∠EDC
D.ED+AC>AD
8.如图,在等边三角形ABC中,中线AD,BE交于F,则图中共有等腰三角形(
)
A.3个
B.4个
C.5个
D.6个
9.如图,AD是△ABC的中线,∠ADC=60°,把△ADC沿直线AD折过来,点C落在C′位置,当BC=4时,BC′的长(
)
A.等于2
B.大于2
C.小于2
D.大于2且小于4
第9题图
第10题图
10.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法:①AD是△ABC的角平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC∶S△ABC=1∶3,其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题3分,共24分)
11.如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是(
).
第11题图
第13题图
第14题图
第15题图
12.已知∠α和线段m、n,求作△ABC,使BC=m,AB=n,∠ABC=∠α.作法的合理顺序为(
).(填序号)
①在射线BD上截取线段BA=n;②作一条线段BC=m;③以B为顶点,以BC为一边,作角∠DBC=∠α;④连结AC,△ABC就是所求作的三角形.
13.如图,在△ABC中,BC边的垂直平分线交BC于D,交AB于E,若CE平分∠ACB,∠B=40°,则∠A=(
)度.
14.(2016·济宁)如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:(
),使△AEH≌△CEB.
15.如图,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=(
).
16.若等腰三角形一腰上的高与另一腰的夹角为45°,则它的一个底角的度数是(
).
17.如图,AD∥BC,∠ABC的角平分线BP与∠BAO的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为(
).
第17题图
第18题图
18.如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM,下列结论:①AP=CE;②∠PME=60°;③BM平分∠AME;④AM+MC=BM.其中正确的有(
).(填序号)
三、解答题(共66分)
19.(8分)(2016·重庆)如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.
20.(9分)如图,在△ABC中,点D是∠BAC的角平分线上一点,BD⊥AD于点D,过点D作DE∥AC交AB于点E.试判断△BED的形状,并说明理由.
21.(8分)有公路l1同侧、l2异侧的两个城镇A,B,如图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点.(保留作图痕迹,不要求写出作法)
.
22.(9分)如图①,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图②,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其他条件不变.求证:△AEF≌△BCF.
23.(10分)如图,已知△ABC中BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交AC于点G.求证:
(1)BF=CG;
(2)AF=(AB+AC).
24.(10分)如图,已知点D为等腰Rt△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
25.(12分)已知△ABC是边长为4
cm的等边三角形,现有两动点P、Q,其中点P从顶点A出发,沿射线AB运动,点Q从顶点B同时出发,沿射线BC运动,且它们的速度都为1
cm/s,经过A、Q的直线与经过C、P的直线交于点M,
(1)当点P在线段AB上移动时,如图,
①试判定线段AP与BQ的数量关系;(直接写出结果)
②试说明△ABQ≌△CAP;
(2)试探索:在P、Q运动的过程中,∠CMQ的大小变化吗?若变化,请说明理由;若不变,求出它的度数.
第13章检测题(答案版)
时间:120分钟 满分:120分
一、选择题(每小题3分,共30分)
1.下列命题的逆命题中是假命题的是(
B
)
A.有一个内角等于60°的等腰三角形是等边三角形
B.对顶角相等
C.线段垂直平分线上的点到这条线段两个端点的距离相等
D.角的内部到角的两边距离相等的点在这个角的平分线上
2.如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是(
C
)
A.AB=DE
B.AC=DF
C.∠A=∠D
D.BF=EC
第2题图
第3题图
第5题图
3.如图,∠1=∠2,∠3=∠4,则下面结论中错误的是(
C
)
A.△ADC≌△BCD
B.△ABD≌△BAC
C.△ABO≌△COD
D.△AOD≌△BOC
4.用尺规作图:“已知底边和底边上的高,求作等腰三角形”,有下列作法:①作线段BC=a;②作线段BC的垂直平分线m,交BC于点D;③在直线m上截取DA=h,连结AB,AC.这样作法的根据是(
A
)
A.线段垂直平分线上的点到线段两个端点的距离相等
B.角平分线上的点到这个角两边的距离相等
C.等角对等边
D.等腰三角形的对称性
5.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19
cm,△ABD的周长为13
cm,则AE的长为(
A
)
A.3
cm
B.6
cm
C.12
cm
D.16
cm
6.如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为(
D
)
A.50°
B.51°
C.51.5°
D.52.5°
第6题图
第7题图
第8题图
7.如图,已知AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是(
B
)
A.BD+ED=BC
B.∠B=2∠DAC
C.AD平分∠EDC
D.ED+AC>AD
8.如图,在等边三角形ABC中,中线AD,BE交于F,则图中共有等腰三角形(
D
)
A.3个
B.4个
C.5个
D.6个
9.如图,AD是△ABC的中线,∠ADC=60°,把△ADC沿直线AD折过来,点C落在C′位置,当BC=4时,BC′的长(
A
)
A.等于2
B.大于2
C.小于2
D.大于2且小于4
第9题图
第10题图
10.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法:①AD是△ABC的角平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC∶S△ABC=1∶3,其中正确的有(
D
)
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题3分,共24分)
11.如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是__A.S.A.__.
第11题图
第13题图
第14题图
第15题图
12.已知∠α和线段m、n,求作△ABC,使BC=m,AB=n,∠ABC=∠α.作法的合理顺序为__②③①④__.(填序号)
①在射线BD上截取线段BA=n;②作一条线段BC=m;③以B为顶点,以BC为一边,作角∠DBC=∠α;④连结AC,△ABC就是所求作的三角形.
13.如图,在△ABC中,BC边的垂直平分线交BC于D,交AB于E,若CE平分∠ACB,∠B=40°,则∠A=__60__度.
14.(2016·济宁)如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:__AH=CB或EH=EB或AE=CE(只要符合要求即可)__,使△AEH≌△CEB.
15.如图,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=__27°__.
16.若等腰三角形一腰上的高与另一腰的夹角为45°,则它的一个底角的度数是__22.5°或67.5°__.
17.如图,AD∥BC,∠ABC的角平分线BP与∠BAO的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为__4__.
第17题图
第18题图
18.如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM,下列结论:①AP=CE;②∠PME=60°;③BM平分∠AME;④AM+MC=BM.其中正确的有__①②③④__.(填序号)
三、解答题(共66分)
19.(8分)(2016·重庆)如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.
证明:∵AB∥CD,∴∠BAC=∠ECD.在△ABC和△CED中,,∴△ABC≌△CED(S.A.S.)∴∠B=∠E.
20.(9分)如图,在△ABC中,点D是∠BAC的角平分线上一点,BD⊥AD于点D,过点D作DE∥AC交AB于点E.试判断△BED的形状,并说明理由.
解:△BED是等腰三角形.理由:∵DE∥AC,∴∠CAD=∠EDA.∵∠CAD=∠DAE,∴∠EDA=∠EAD.∵∠EAD+∠EBD=90°,∠EDA+∠EDB=90°,∴∠EBD=∠EDB,∴EB=ED,∴△BED是等腰三角形.
21.(8分)有公路l1同侧、l2异侧的两个城镇A,B,如图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点.(保留作图痕迹,不要求写出作法)
解:如图.
点C1,C2就是符合条件的点.
22.(9分)如图①,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图②,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其他条件不变.求证:△AEF≌△BCF.
证明:(1)∵AB=AC,D是BC的中点,∴∠BAE=∠EAC.在△ABE和△ACE中,
∴△ABE≌△ACE(S.A.S.),∴BE=CE.
(2)∵∠BAC=45°,BF⊥AF,∴△ABF为等腰直角三角形,∴AF=BF.∵AB=AC,点D是BC的中点,∴AD⊥BC,∴∠EAF+∠C=90°.∵BF⊥AC,∴∠CBF+∠C=90°.∴∠EAF=∠CBF.
在△AEF和△BCF中,∴△AEF≌△BCF(A.S.A.)
23.(10分)如图,已知△ABC中BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交AC于点G.求证:
(1)BF=CG;
(2)AF=(AB+AC).
证明:(1)连结BE,CE.∵AE平分∠BAC,EF⊥AB,EG⊥AC,∴EF=EG,∵DE垂直平分BC,∴EB=EC.在Rt△EFB和Rt△EGC中,∴Rt△EFB≌Rt△EGC(H.L.),∴BF=CG.
(2)∵BF=CG,∴AB+AC=AB+BF+AG=AF+AG.又易证Rt△AEF≌Rt△AEG(H.L.),∴AF=AG,∴AF=(AB+AC).
24.(10分)如图,已知点D为等腰Rt△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
解:(1)∵△ABC为等腰直角三角形,∴AC=BC,∠CAB=∠CBA=45°.又∠CAD=∠CBD=15°,∴∠DAB=∠DBA=30°,∴DA=DB.又CD=CD,∴△ACD≌△BCD(S.S.S.),∴∠ACD=∠BCD=∠ACB=45°.∵∠CDE=∠CAD+∠ACD=15°+45°=60°,∠BDE=∠DAB+∠DBA=30°+30°=60°,∴∠CDE=∠BDE,即DE平分∠BDC.
(2)连结CM,由(1)知,∠CDE=60°,又DC=DM,∴△CDM是等边三角形,∴CM=CD,∠CMD=60°.∵CE=CA,∴∠E=∠CAD=15°,∴∠ECM=∠CMD-∠E=60°-15°=45°,∴∠ECM=∠BCD=45°.又CE=CA=CB,∴△BCD≌△ECM(S.A.S.),∴EM=BD.
25.(12分)已知△ABC是边长为4
cm的等边三角形,现有两动点P、Q,其中点P从顶点A出发,沿射线AB运动,点Q从顶点B同时出发,沿射线BC运动,且它们的速度都为1
cm/s,经过A、Q的直线与经过C、P的直线交于点M,
(1)当点P在线段AB上移动时,如图,
①试判定线段AP与BQ的数量关系;(直接写出结果)
②试说明△ABQ≌△CAP;
(2)试探索:在P、Q运动的过程中,∠CMQ的大小变化吗?若变化,请说明理由;若不变,求出它的度数.
解:(1)①AP=BQ.②∵等边三角形ABC中,AB=AC,∠ABC=∠CAP=60°,又由条件得AP=BQ,∴△ABQ≌△CAP(S.A.S.).
(2)①当点P在线段AB上移动时,这时,点Q在线段BC上移动.如图①,∠CMQ的大小不变.
∵△ABQ≌△CAP,∴∠BAQ=∠ACP,
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°.
②当点P在线段AB的延长线上移动时,点Q在线段BC的延长线上移动.如图②,∠CMQ的大小也不变.求法同①,此时∠CMQ=120°.
1
