北师大版数学八年级上册5.1 认识二元一次方程组 课件(38张)
文档属性
| 名称 | 北师大版数学八年级上册5.1 认识二元一次方程组 课件(38张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 16:47:52 | ||
图片预览








文档简介
5.1 认识二元一次方程组
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队为了争取较好名次,想在全部16场比赛中得到28分,那么这个队胜负场数分别是多少?
用学过的一元一次方程能解决此问题吗?
导入新知
这可是两个未知数呀?
1. 了解二元一次方程(组)及其解的定义.
2. 会检验一对数值是不是某个二元一次方程组的解.
素养目标
3. 能根据简单的实际问题列出二元一次方程组.
累死我了!
你还累?这么大的个,才比我多驮了2个.
探究新知
知识点 1
二元一次方程的概念
思考
哼,我从你背上拿来1个,我的包裹数就是你的2倍!
真的?!
思考:听完它们的对话,你能猜出它们各驮了多少包裹吗?
探究新知
问题1 设老牛驮了x个包裹 , 小马驮了y个包裹.你能根据它们的对话列出方程吗?
老牛的包裹数比小马的多2个;
老牛从小马的背上拿来1个包裹,就是小马的2倍.
x-y=2
x+1=2(y-1)
探究新知
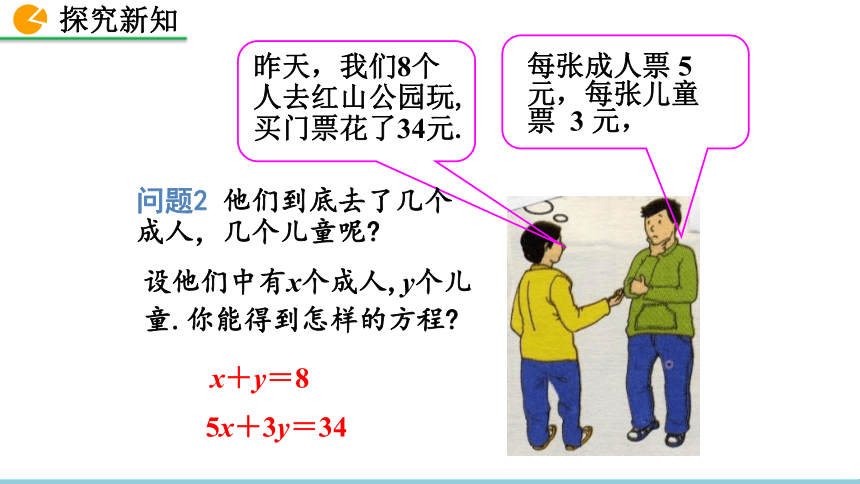
昨天,我们8个人去红山公园玩,买门票花了34元.
每张成人票 5 元,每张儿童票 3 元,
设他们中有x个成人,y个儿童.你能得到怎样的方程?
问题2 他们到底去了几个成人,几个儿童呢?
x+y=8
5x+3y=34
探究新知
1.这四个方程是一元一次方程吗?为什么?
2.这四个方程有什么共同特点?
① 含有两个未知数;
② 含有未知数的项的次数都是1.
二元一次方程
含有两个未知数,并且含有未知数的项的次数都是1的方程叫做二元一次方程.
3.二元一次方程与一元一次方程有什么相同和不同之处?
不同:
相同:
含未知数个数不同
都是一次方程
探究新知
观察思考
x-y=2
x+1=2(y-1)
x+y=8
5x+3y=34
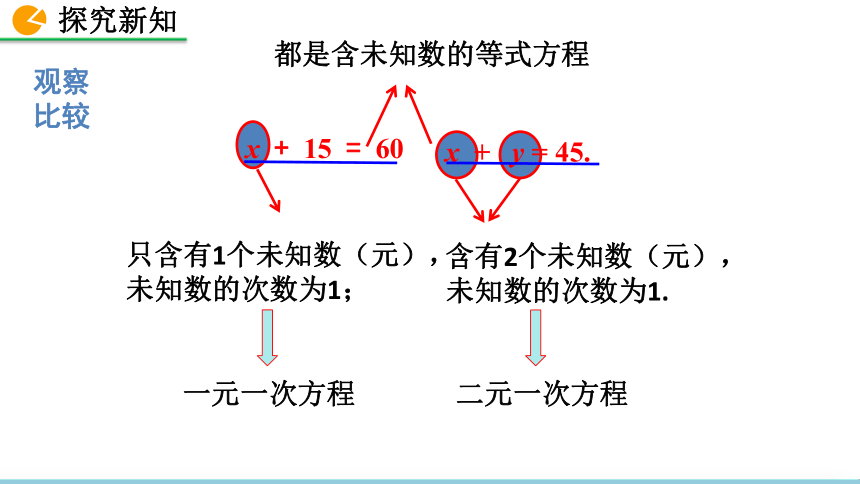
只含有1个未知数(元),未知数的次数为1;
x + y = 45.
x + 15 = 60
含有2个未知数(元),未知数的次数为1.
一元一次方程
都是含未知数的等式方程
二元一次方程
探究新知
观察比较
(3)
(1) 3y-2x =z+5
(4)
(5)
(2)
(6) 3 - 2xy =1
是
不是
不是
不是
不是
不是
例1 判断下列方程是否为二元一次方程:
(7) 4x+ π =0
(8) 2x=1-3y
不是
是
探究新知
素养考点 1
二元一次方程的判断
探究新知
方法点拨
判断一个方程是否为二元一次方程的方法:
一看原方程是否是整式方程且只含有两个未知数;
二看整理化简后的方程是否具备两个未知数的系数都不为0,且含未知数的项的次数都是1.
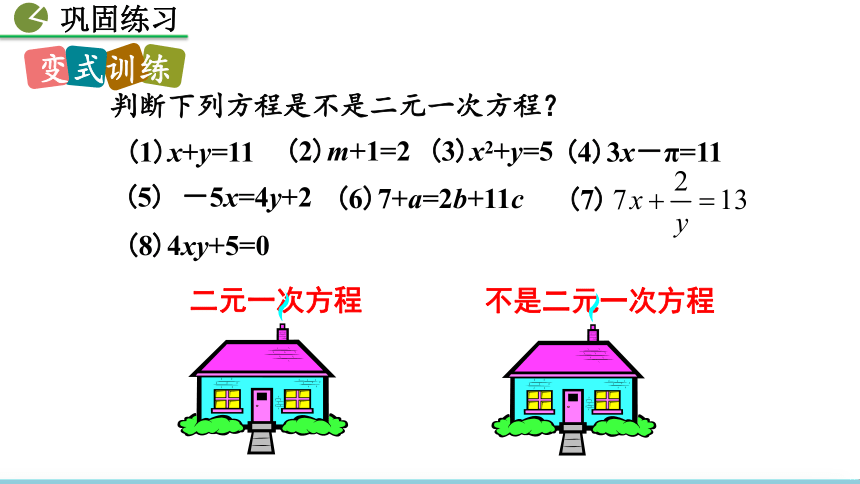
(8)4xy+5=0
(1)x+y=11
(3)x2+y=5
(2)m+1=2
(4)3x-π=11
(5) -5x=4y+2
(6)7+a=2b+11c
二元一次方程
不是二元一次方程
判断下列方程是不是二元一次方程?
巩固练习
(7)
变式训练
例2 已知|m-1|x|m|+y2n-1=3是二元一次方程,
则m+n=________.
解析:根据题意得|m|=1且|m-1|≠0,2n-1=1,解得m=-1,n=1,所以m+n=0.
0
探究新知
素养考点 2
根据二元一次方程的定义求字母的值
方法小结:由方程是二元一次方程可知:
(1)未知数的系数不为0;
(2)未知数的次数都是1.
1.若x2m-1+5y3n-2m =7是二元一次方程,则m=____,n=___.
2m-1=1
1
3n-2m=1
1
巩固练习
2.如果 是二元一次方程,那么k的值是 ( )
A. 2 B. 3 C. 1 D. 0
B
变式训练
x + y = 16
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队为了争取较好名次,想在全部16场比赛中得到28分,那么这个队胜负场数分别是多少?
解:设该队胜了x场,负了y场,根据题意可得方程:
2x + y = 28
等量关系:
胜的场数+负的场数=总场数
胜场积分+负场积分=总积分
探究新知
二元一次方程组的定义
知识点 2
在这两个方程中,x的含义相同吗?y呢?
像这样,共含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.
下列哪些是二元一次方程组?
(1) x+y= 2 (2)
x-y=1 x = y
(3) x=0 (4) z=x+1
y=1 2x-y=5
(5) x-3y=8 (6) 3x=5y
xy=6 2x-y=0
(是)
(是)
(不是)
(不是)
(是)
(不是)
探究新知
通过上面问题,你认为二元一次方程组有哪些特征?
二元一次方程组的特点:
①方程组中共有2个不同未知数;
②方程组有2个一次方程;
③一般用大括号把2个方程连起来.
探究新知
x + y = 16
2x + y = 28
x + y = 2
x – y = 1
例 在方程组
程组的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
D
中,是二元一次方
探究新知
素养考点 1
二元一次方程组的判断
提示:三个要素:
含有两个未知数
含有未知数的项的次数为1
整式方程
下列方程组中,哪些是二元一次方程组_______________
(3)
(5)
(6)
巩固练习
变式训练
x
y
探究 公园门票问题中的方程 x+y=8 ,且符合问题的实际意义的值有哪些?把它们填入表中.
思考1 如果不考虑方程表示的实际意义,还可以取哪些值?这些值是有限的吗?
x
0
1
2
3
4
5
6
7
8
y
8
7
6
5
4
3
2
1
0
x,y还可取到小数,如x=0.5,y=7.5;
有无数组这样的值.
知识点 3
二元一次方程的解的定义
探究新知
适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解.
探究新知
判断一对数值是不是二元一次方程的解,只需把这对数值分别代入方程的左右两边,若左边=右边,则这对数值是这个方程的解;若左边≠右边,则这对数值不是这个方程的解.
温馨提示:一般情况下,二元一次方程有无数组解,但若对其未知数取值附加某些条件,那么也可能只有有限个解.
巩固练习
1.判断给出的x、y的值是否是方程的解
(1) 2x-3y=6 ( ) (2) 5x+2y=8 ( )
×
√
2.在
中, 是方程x+y=22的解的有 (填序号) .
①
②
③
④
⑤
1.上表中列出了公园门票中,满足方程x+y=8,且符合实际意义的值.
0
8
2
1
3
6
4
5
7
8
7
1
4
2
5
6
3
0
x
y
x
y
8
2
5
3
2.再找出方程5x +3y = 34的符合实际意义的解,并用表格罗列.
探究新知
知识点 4
二元一次方程组的解的定义
注意:这里的x 、y,都代表人数,所以只能取正整数
二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解.
思考 观察两个表格你有什么发现?
x=5,y=3是方程x+y=8 ①与方程5x+3y=34 ②的公共解,记作 .
探究新知
x = 5
y = 3
0
8
2
1
3
6
4
5
7
8
7
1
4
2
5
6
3
0
x
y
x
y
8
2
5
3
1.填表:使每对x,y的值是方程3x+y=5的解.
2.已知下列三对数值
________是方程x+y=7的解;
________是方程2x+y=9的解,
_______是方程组 的解.
x
-2
0
0.4
2
y
-0.4
-1
0.5
2
11
5
3.8
-1
1.8
2
1
x=2
y=5
x=1
y=7
x + y=7
2x+y=9
x=2
y=5
1.5
x=1
y=6
x=2
y=5
x=1
y=7
,
,
x=2
y=5
x=1
y=6
巩固练习
解:把 代入到方程组,得:
解得a =2,b=11.
x = 1
y =-2
例1 已知二元一次方程组 的解是
求a与b的值.
探究新知
素养考点 1
利用二元一次方程组的解求字母的值
若 是方程x-ky=1的解,则k的值为 .
解析:将 代入原方程得-2-3k=1,解得k=-1.
{
x=-2,
y=3
-1
巩固练习
{
x=-2,
y=3
变式训练
引导学生读懂数学书课题研究成果配套课件
课件制作:吴秀青
例2 对下面的问题,列出二元一次方程组,并根据问题的实际意义,找出问题的解.加工某种产品需经两道工序,第一道工序每人每天可完成900件,第二道工序每人每天可完成1200件.现有7位工人参加这两道工序,应怎样安排人力,才能使每天第一、第二道工序所完成的件数相等?
探究新知
素养考点 2
根据实际问题列二元一次方程组
引导学生读懂数学书课题研究成果配套课件
课件制作:吴秀青
分析:第一道工序的人数+ _______________ =总人数;
第一道工序的件数=________________.
设安排第一道工序x人,第二道工序y人,用方程把这些条件表示出来:
? ?___________.
x+y=7
900x=1200y
第二道工序的人数
第二道工序的件数
解:所以可列方程组为
探究新知
是该问题的解.
根据以下对话,可以求得小红所买的笔和笔记本的价格分别是( )
哦……我忘了!只记得先后买了两次,第一次买了5支笔和10本笔记本花了42元钱,第二次买了10支笔和5本笔记本花了30元钱.
小红,你上周买的笔和笔记本的价格是多少啊?
D
A.0.8元/支,2.6元/本
B.0.8元/支,3.6元/本
C.1.2元/支,2.6元/本
D.1.2元/支,3.6元/本
设小红所买的笔和笔记本的价格分别为x元和y元,可列 将选项代入判断是否是方程组的解.
巩固练习
变式训练
(2019?天津)方程组 的解是( )
A. B.
C. D.
D
连接中考
1.方程 5x+y=0,2x+xy=1,7x+y-2x=0,x2-x+1=0中,二元一次方程的个数是 ( )
A. 1个 B. 2个
C. 3个 D. 4个
B
基础巩固题
课堂检测
2.下列方程组中是二元一次方程组的是 ( )
C
课堂检测
A.
B.
C.
D.
基础巩固题
3. 解为 的方程组是 ( )
D
课堂检测
A.
B.
C.
D.
基础巩固题
4.小刘同学用10元钱购买了两种不同的贺卡共8张,
单价分别是1元与2元.设他购买了1元的贺卡x张,
2元的贺卡y张,那么可列方程组( )
A. B.
C. D.
D
基础巩固题
课堂检测
1.已知 是方程2x-4y+2a=3的一组解,则
a=____.
2.若方程2x2m+3+3y3n-7=0 是关于x、y的二元一次方程,则m=______,n=______;
x=3,
y=1
-1
能力提升题
课堂检测
把一根长13m的钢管截成2m长或3m长两种规格的钢管,怎样截不造成浪费?你有几种不同的截法?
解:设截成2m长的钢管x根,3m长的钢管y根,
则2x+3y=13,
因为x,y均为非负整数,所以 或
故有2种不同的截法:
3m长1根、2m长5根以及3m长3根、2m长2根.
x=5,
y=1
x=2,
y=3
拓广探索题
课堂检测
认识二元一次方程组
二元一次方程及二元一次方程组的定义
二元一次方程及二元一次方程组的解
根据实际问题列二元一次方程组
课堂小结
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队为了争取较好名次,想在全部16场比赛中得到28分,那么这个队胜负场数分别是多少?
用学过的一元一次方程能解决此问题吗?
导入新知
这可是两个未知数呀?
1. 了解二元一次方程(组)及其解的定义.
2. 会检验一对数值是不是某个二元一次方程组的解.
素养目标
3. 能根据简单的实际问题列出二元一次方程组.
累死我了!
你还累?这么大的个,才比我多驮了2个.
探究新知
知识点 1
二元一次方程的概念
思考
哼,我从你背上拿来1个,我的包裹数就是你的2倍!
真的?!
思考:听完它们的对话,你能猜出它们各驮了多少包裹吗?
探究新知
问题1 设老牛驮了x个包裹 , 小马驮了y个包裹.你能根据它们的对话列出方程吗?
老牛的包裹数比小马的多2个;
老牛从小马的背上拿来1个包裹,就是小马的2倍.
x-y=2
x+1=2(y-1)
探究新知
昨天,我们8个人去红山公园玩,买门票花了34元.
每张成人票 5 元,每张儿童票 3 元,
设他们中有x个成人,y个儿童.你能得到怎样的方程?
问题2 他们到底去了几个成人,几个儿童呢?
x+y=8
5x+3y=34
探究新知
1.这四个方程是一元一次方程吗?为什么?
2.这四个方程有什么共同特点?
① 含有两个未知数;
② 含有未知数的项的次数都是1.
二元一次方程
含有两个未知数,并且含有未知数的项的次数都是1的方程叫做二元一次方程.
3.二元一次方程与一元一次方程有什么相同和不同之处?
不同:
相同:
含未知数个数不同
都是一次方程
探究新知
观察思考
x-y=2
x+1=2(y-1)
x+y=8
5x+3y=34
只含有1个未知数(元),未知数的次数为1;
x + y = 45.
x + 15 = 60
含有2个未知数(元),未知数的次数为1.
一元一次方程
都是含未知数的等式方程
二元一次方程
探究新知
观察比较
(3)
(1) 3y-2x =z+5
(4)
(5)
(2)
(6) 3 - 2xy =1
是
不是
不是
不是
不是
不是
例1 判断下列方程是否为二元一次方程:
(7) 4x+ π =0
(8) 2x=1-3y
不是
是
探究新知
素养考点 1
二元一次方程的判断
探究新知
方法点拨
判断一个方程是否为二元一次方程的方法:
一看原方程是否是整式方程且只含有两个未知数;
二看整理化简后的方程是否具备两个未知数的系数都不为0,且含未知数的项的次数都是1.
(8)4xy+5=0
(1)x+y=11
(3)x2+y=5
(2)m+1=2
(4)3x-π=11
(5) -5x=4y+2
(6)7+a=2b+11c
二元一次方程
不是二元一次方程
判断下列方程是不是二元一次方程?
巩固练习
(7)
变式训练
例2 已知|m-1|x|m|+y2n-1=3是二元一次方程,
则m+n=________.
解析:根据题意得|m|=1且|m-1|≠0,2n-1=1,解得m=-1,n=1,所以m+n=0.
0
探究新知
素养考点 2
根据二元一次方程的定义求字母的值
方法小结:由方程是二元一次方程可知:
(1)未知数的系数不为0;
(2)未知数的次数都是1.
1.若x2m-1+5y3n-2m =7是二元一次方程,则m=____,n=___.
2m-1=1
1
3n-2m=1
1
巩固练习
2.如果 是二元一次方程,那么k的值是 ( )
A. 2 B. 3 C. 1 D. 0
B
变式训练
x + y = 16
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队为了争取较好名次,想在全部16场比赛中得到28分,那么这个队胜负场数分别是多少?
解:设该队胜了x场,负了y场,根据题意可得方程:
2x + y = 28
等量关系:
胜的场数+负的场数=总场数
胜场积分+负场积分=总积分
探究新知
二元一次方程组的定义
知识点 2
在这两个方程中,x的含义相同吗?y呢?
像这样,共含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.
下列哪些是二元一次方程组?
(1) x+y= 2 (2)
x-y=1 x = y
(3) x=0 (4) z=x+1
y=1 2x-y=5
(5) x-3y=8 (6) 3x=5y
xy=6 2x-y=0
(是)
(是)
(不是)
(不是)
(是)
(不是)
探究新知
通过上面问题,你认为二元一次方程组有哪些特征?
二元一次方程组的特点:
①方程组中共有2个不同未知数;
②方程组有2个一次方程;
③一般用大括号把2个方程连起来.
探究新知
x + y = 16
2x + y = 28
x + y = 2
x – y = 1
例 在方程组
程组的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
D
中,是二元一次方
探究新知
素养考点 1
二元一次方程组的判断
提示:三个要素:
含有两个未知数
含有未知数的项的次数为1
整式方程
下列方程组中,哪些是二元一次方程组_______________
(3)
(5)
(6)
巩固练习
变式训练
x
y
探究 公园门票问题中的方程 x+y=8 ,且符合问题的实际意义的值有哪些?把它们填入表中.
思考1 如果不考虑方程表示的实际意义,还可以取哪些值?这些值是有限的吗?
x
0
1
2
3
4
5
6
7
8
y
8
7
6
5
4
3
2
1
0
x,y还可取到小数,如x=0.5,y=7.5;
有无数组这样的值.
知识点 3
二元一次方程的解的定义
探究新知
适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解.
探究新知
判断一对数值是不是二元一次方程的解,只需把这对数值分别代入方程的左右两边,若左边=右边,则这对数值是这个方程的解;若左边≠右边,则这对数值不是这个方程的解.
温馨提示:一般情况下,二元一次方程有无数组解,但若对其未知数取值附加某些条件,那么也可能只有有限个解.
巩固练习
1.判断给出的x、y的值是否是方程的解
(1) 2x-3y=6 ( ) (2) 5x+2y=8 ( )
×
√
2.在
中, 是方程x+y=22的解的有 (填序号) .
①
②
③
④
⑤
1.上表中列出了公园门票中,满足方程x+y=8,且符合实际意义的值.
0
8
2
1
3
6
4
5
7
8
7
1
4
2
5
6
3
0
x
y
x
y
8
2
5
3
2.再找出方程5x +3y = 34的符合实际意义的解,并用表格罗列.
探究新知
知识点 4
二元一次方程组的解的定义
注意:这里的x 、y,都代表人数,所以只能取正整数
二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解.
思考 观察两个表格你有什么发现?
x=5,y=3是方程x+y=8 ①与方程5x+3y=34 ②的公共解,记作 .
探究新知
x = 5
y = 3
0
8
2
1
3
6
4
5
7
8
7
1
4
2
5
6
3
0
x
y
x
y
8
2
5
3
1.填表:使每对x,y的值是方程3x+y=5的解.
2.已知下列三对数值
________是方程x+y=7的解;
________是方程2x+y=9的解,
_______是方程组 的解.
x
-2
0
0.4
2
y
-0.4
-1
0.5
2
11
5
3.8
-1
1.8
2
1
x=2
y=5
x=1
y=7
x + y=7
2x+y=9
x=2
y=5
1.5
x=1
y=6
x=2
y=5
x=1
y=7
,
,
x=2
y=5
x=1
y=6
巩固练习
解:把 代入到方程组,得:
解得a =2,b=11.
x = 1
y =-2
例1 已知二元一次方程组 的解是
求a与b的值.
探究新知
素养考点 1
利用二元一次方程组的解求字母的值
若 是方程x-ky=1的解,则k的值为 .
解析:将 代入原方程得-2-3k=1,解得k=-1.
{
x=-2,
y=3
-1
巩固练习
{
x=-2,
y=3
变式训练
引导学生读懂数学书课题研究成果配套课件
课件制作:吴秀青
例2 对下面的问题,列出二元一次方程组,并根据问题的实际意义,找出问题的解.加工某种产品需经两道工序,第一道工序每人每天可完成900件,第二道工序每人每天可完成1200件.现有7位工人参加这两道工序,应怎样安排人力,才能使每天第一、第二道工序所完成的件数相等?
探究新知
素养考点 2
根据实际问题列二元一次方程组
引导学生读懂数学书课题研究成果配套课件
课件制作:吴秀青
分析:第一道工序的人数+ _______________ =总人数;
第一道工序的件数=________________.
设安排第一道工序x人,第二道工序y人,用方程把这些条件表示出来:
? ?___________.
x+y=7
900x=1200y
第二道工序的人数
第二道工序的件数
解:所以可列方程组为
探究新知
是该问题的解.
根据以下对话,可以求得小红所买的笔和笔记本的价格分别是( )
哦……我忘了!只记得先后买了两次,第一次买了5支笔和10本笔记本花了42元钱,第二次买了10支笔和5本笔记本花了30元钱.
小红,你上周买的笔和笔记本的价格是多少啊?
D
A.0.8元/支,2.6元/本
B.0.8元/支,3.6元/本
C.1.2元/支,2.6元/本
D.1.2元/支,3.6元/本
设小红所买的笔和笔记本的价格分别为x元和y元,可列 将选项代入判断是否是方程组的解.
巩固练习
变式训练
(2019?天津)方程组 的解是( )
A. B.
C. D.
D
连接中考
1.方程 5x+y=0,2x+xy=1,7x+y-2x=0,x2-x+1=0中,二元一次方程的个数是 ( )
A. 1个 B. 2个
C. 3个 D. 4个
B
基础巩固题
课堂检测
2.下列方程组中是二元一次方程组的是 ( )
C
课堂检测
A.
B.
C.
D.
基础巩固题
3. 解为 的方程组是 ( )
D
课堂检测
A.
B.
C.
D.
基础巩固题
4.小刘同学用10元钱购买了两种不同的贺卡共8张,
单价分别是1元与2元.设他购买了1元的贺卡x张,
2元的贺卡y张,那么可列方程组( )
A. B.
C. D.
D
基础巩固题
课堂检测
1.已知 是方程2x-4y+2a=3的一组解,则
a=____.
2.若方程2x2m+3+3y3n-7=0 是关于x、y的二元一次方程,则m=______,n=______;
x=3,
y=1
-1
能力提升题
课堂检测
把一根长13m的钢管截成2m长或3m长两种规格的钢管,怎样截不造成浪费?你有几种不同的截法?
解:设截成2m长的钢管x根,3m长的钢管y根,
则2x+3y=13,
因为x,y均为非负整数,所以 或
故有2种不同的截法:
3m长1根、2m长5根以及3m长3根、2m长2根.
x=5,
y=1
x=2,
y=3
拓广探索题
课堂检测
认识二元一次方程组
二元一次方程及二元一次方程组的定义
二元一次方程及二元一次方程组的解
根据实际问题列二元一次方程组
课堂小结
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
