北师版数学八年级上册第三章《位置与坐标》测试题(Word版 含答案)
文档属性
| 名称 | 北师版数学八年级上册第三章《位置与坐标》测试题(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 304.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 21:30:42 | ||
图片预览



文档简介
北师版数学八年级上册《位置与坐标》测试题
一、选择题(精心选,答案唯一,每题3分,满分30分)
1.下列描述中,能确定位置的是
(
)
A.小明的电影票是第三排
B.小亮的家在小明家的西北方向
C.轮船A在B港南偏东50°方向,同时在C港北偏东60°方向
D.
北京大兴国际机场在北京的南面
2.
(2019?株洲)在平面直角坐标系中,点A(2,–3)位于哪个象限?(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.
(2019?浙江杭州)在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则
( )
A.m=3,n=2
B.m=-3,n=2
C.m=2,n=3
D.m=-2,n=-3
4.已知点A(3,m),B(3,n),则下面说法中,正确的是
(
)
A.A,B一定不是同一个点
B.经过A,B的直线平行于x轴
C.
经过A,B的直线平行于y轴
D.A,B两点可在x轴的负半轴
5.
(2019?浙江丽水)如图1是雷达屏幕在一次探测中发现的多个目标,其中对目标A的位置表述正确的是
( )
A.在南偏东75°方向处
B.在5km处
C.在南偏东15°方向5km处
D.在南偏东75°方向5km处
6.
(2019?甘肃)已知点P(m+2,2m﹣4)在x轴上,则点P的坐标是
(
)
A.(4,0)
B.(0,4)
C.(﹣4,0)
D.(0,﹣4)
7.
已知点A(,|a|),则点A的位置是
(
)
A.第一象限
B.第四象限
C.第一象限或x轴的正半轴
D.
第四象限或x轴的负半轴
8.已知点A(x,
)在坐标轴上,则满足条件的点A的个数为
(
)
A.1个
B.
2个
C.
3个
D.
4个
9.
已知点M(2a-1,3a+2),N(-1,4),且直线MN∥y轴,则的值为
(
)
A.0
B.1
C.
D.
?
10.如图2,已知点A(3,0),点(-3,0),点P是△AOB内部一点,且坐标为(a,b),
则点P在△O内的对应点的坐标为
(
)
A.(b,a)
B.(-a,b)
C.
(a,-b)
D.
(-b,a)
二、填空题(仔细填,考虑全,每题3分,满分18分)
11.
(2019?山东省济宁市
)已知点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),
写出一个符合上述条件的点P的坐标
.
12.
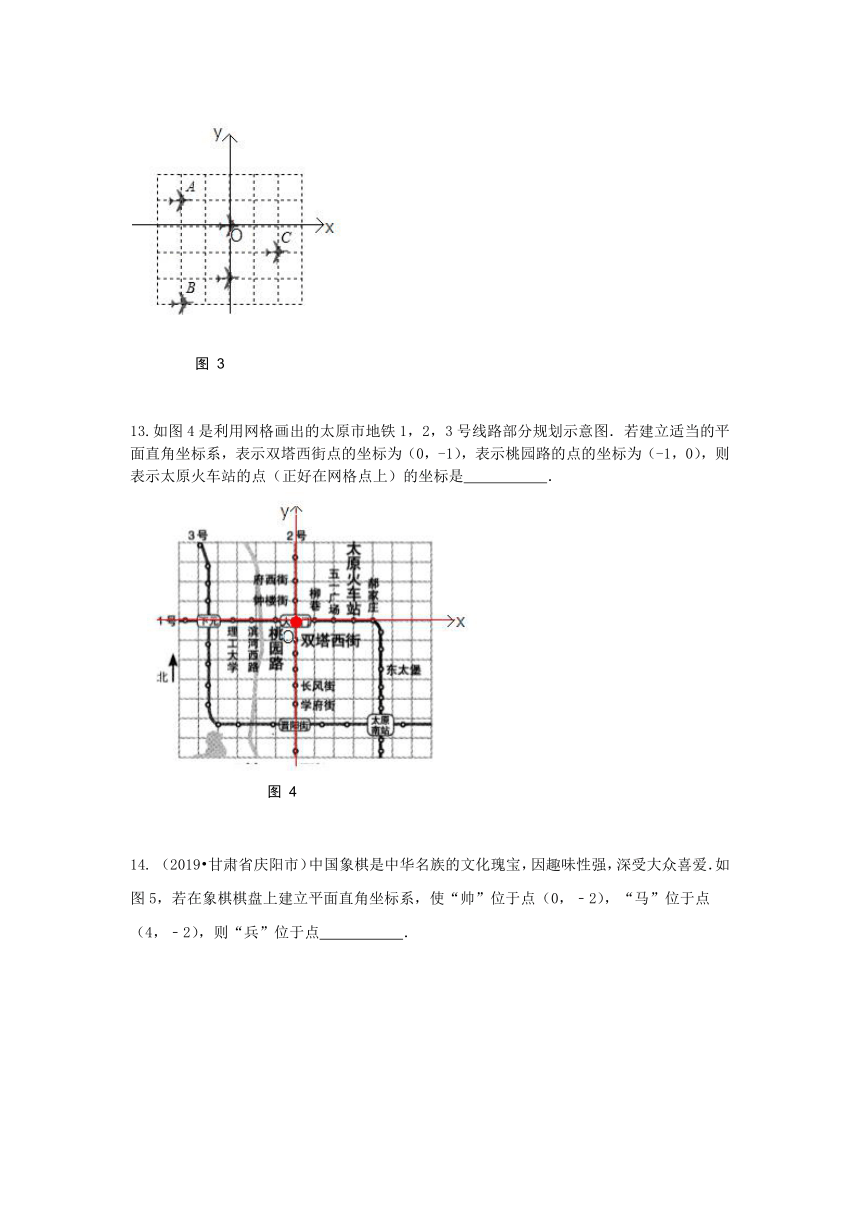
如图3是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么第一架轰炸机C的平面坐标是
.
图
3
13.如图4是利用网格画出的太原市地铁1,2,3号线路部分规划示意图.若建立适当的平面直角坐标系,表示双塔西街点的坐标为(0,-1),表示桃园路的点的坐标为(-1,0),则表示太原火车站的点(正好在网格点上)的坐标是
.
图
4
14.
(2019?甘肃省庆阳市)中国象棋是中华名族的文化瑰宝,因趣味性强,深受大众喜爱.如
图5,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,﹣2),“马”位于点
(4,﹣2),则“兵”位于点
.
15.
(2019?山东临沂)在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是
.
16.
已知点A(3,4),B(a,4)之间的距离为4,则a的值为
.
三、解答题(规范解,求准确,满分52分)
17.
(满分6分)(2019?湖北黄石)若点P的坐标为(,2x﹣9),其中x满足不等式组,求点P所在的象限.
18.
(满分6分)
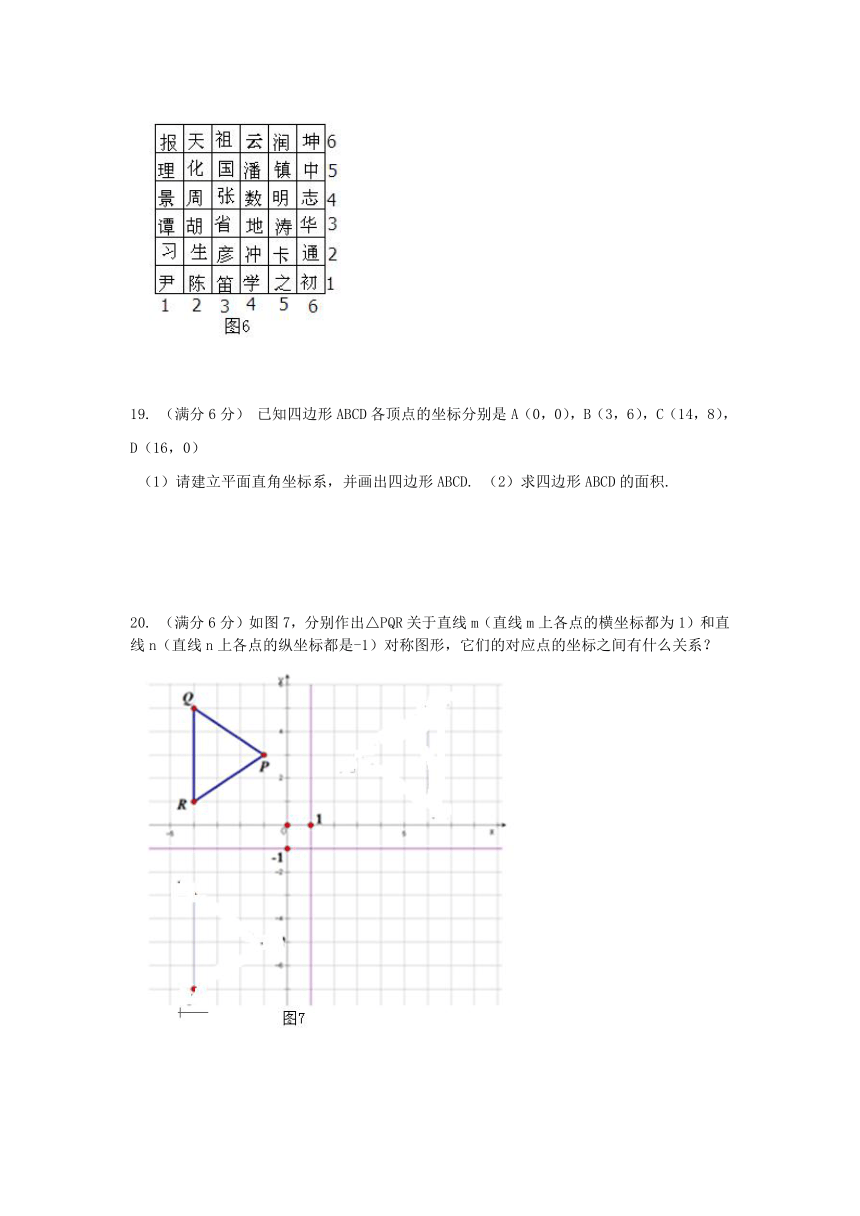
如图6,在6×6网格中,填写不同的汉字,并且每一个汉字都对应一个密码,如“国”的密码是(3,5),“涛”的密码是(5,3),当你理解了密码后,请把下列密码翻译出来,连起来读一读,猜猜他们是谁?一定会有惊喜.
(1)(3,6),(4,2),(5,1);
(2)
(2,1),(1,4),(5,6);
(3)
(3,1),(5,2)和(1,6);
(4)(6,5),(4,1),(2,2),
(4,1),(1,2),(1,6).
19.
(满分6分)
已知四边形ABCD各顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0)
(1)请建立平面直角坐标系,并画出四边形ABCD.
(2)求四边形ABCD的面积.
20.
(满分6分)如图7,分别作出△PQR关于直线m(直线m上各点的横坐标都为1)和直线n(直线n上各点的纵坐标都是-1)对称图形,它们的对应点的坐标之间有什么关系?
21.
(满分6分)
如图8,三角形AOB中,A、B两点的坐标分别是(2,4),(6,2),求三角形AOB的面积.
22.
(满分7分)
在平面直角坐标系xoy中的点P(x,y),若点Q的坐标(x+ay,ax+y),其中,a是常数,且a≠0,则称点Q是点P的“a系联动点”.例如,点(1,2)的“3系联动点”点Q的坐标为(7,5).
(1)点(3,0)的“2系联动点”的坐标为
;若点P的“-2系联动点”的坐标为(-3,0),
则点P的坐标为
;
(2)若点P的“a系联动点”与“-a系联动点”,均关于x轴对称,则点P分布在
;
请证明这个结论;
(3)在(2)的条件下,点P与原点不重合,点P的“a系联动点”
是点Q,且PQ的长度是OP长度的3倍,求a的值.
23.
(满分7分)
(2019?河北省)勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图9(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为
km;
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为
km.
24.
(满分7分)先阅读下列一段文字,再解答问题
已知在平面内有两点,,其两点间的距离公式为,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为或
(1)已知点,,试求,两点间的距离;
(2)已知点,在平行于轴的直线上,点的纵坐标为,点的纵坐标为,试求,两点间的距离;
(3)已知点,,判断线段,,构成三角形的形状?并求图形的面积.
参考答案:
一、选择题
1.C
2.
D
3.
B
4.C
5.
D
6.
A
7.
C
8.C
9.
B
10.B
二、填空题
11.
解:(1,﹣2)(答案不唯一).
提示:∵点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),
∴x>0,y<0,∴当x=1时,1≤y+4,解得:0>y≥﹣3,∴y可以为:﹣2,
故写一个符合上述条件的点P的坐标可以为:(1,﹣2)(答案不唯一).
12.
解:(2,﹣1).
13.
解:(3,0)
提示:双塔西街点的坐标为(0,-1),桃园路的点的坐标为(-1,0),所以大南门为坐标原点,所以太原火车站的点(正好在网格点上)的坐标(3,0).
14.
解:(﹣1,1).
15.
解:(-1,2).
提示:设点P(4,2)关于直线x=1的对称点坐标为Q(,2),根据题意,得,解得,=-2,所以点P(4,2)关于直线x=1的对称点坐标为Q(-1,2).
16.
解:a=-1或a=7.
三、解答题
17.
解:,解①得:x≥4,解②得:x≤4,则不等式组的解是:x=4,
∵=1,2x﹣9=﹣1,∴点P的坐标为(1,﹣1),∴点P在的第四象限.
18.
解:由“国”的密码是(3,5),“涛”的密码是(5,3),
知道,密码的设计是:第一个数字所在的列,与第二个数字所在行的交叉点上的字,就是我们需要的答案,根据这条原则,我们不难解答给出的问题.
(1)祖冲之;
(2)
陈景润;
(3)笛卡尔;(4)《中学生学习报》.
19.
解:
(1)建立坐标系如下:
(2)如图所示,分割图形后,得四边形的面积=80.
.
20.
解:
仔细观察坐标系,得P(-1,3),Q(-4,5),R(-4,1),设P(-1,3)关于直线m=1的对称点的坐标为(,3),根据对称等距性,得-1=1-(-1),解得=3,所以(3,3),
同理可得,(6,5),(6,1),所以△PQR关于直线m的对称图形为△;
仔细观察坐标系,得P(-1,3),Q(-4,5),R(-4,1),设P(-1,3)关于直线n=-1的对称点的坐标为(-1,),根据对称等距性,得3-(-1)=-1-,解得=-5,所以(-1,-5),同理可得,(-4,-7),(-4,-3),所以△PQR关于直线n的对称图形为△;作图如图所示;
21.
解:
方法1:
如图1,过点A作AE⊥y轴,垂足为E,过点B作BD⊥x轴,垂足为D,二线交于点C,因为点A的坐标为(2,4),所以点E的坐标为(0,4),所以OE=4,因为点C在直线AE上,所以点C的纵坐标为4;因为点B的坐标为(6,2),所以点C的横坐标为6,所以点C的坐标为(6,4),
所以AE=-=2-0=2,AC==6-2=4,CB==4-2=2,BD==2-0=2,OD==4-0=4,所以四边形OECD的面积为:6×4=24,===4,===4,===6,
所以=四边形OECD的面积---=24-4-4-6=10.
方法2:
如图2过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,因为点A的坐标为(2,4),所以点C的坐标为(2,0),所以OC=2,AC=4,因为点B的坐标为(6,2),所以点D的横坐标为6,所以点D的坐标为(6,0),BD==2-0=2,OD==6-0=6,CD==6-2=4,所以===4,
===6,直角梯形ABDC的面积为:=12,
所以=直角梯形ABDC的面积+-=12+4-6=10.
22.
解:
(1)因为x=3,y=0,a=2,所以x+ay=3+0×2=3,ax+y=3×2+0=6,
所以点(3,0)的“2系联动点”的坐标为(3,6);
因为点P的“-2系联动点”的坐标为(-3,0),所以x-2y=-3,-2x+y=0,所以x=1,y=2,
所以点P的坐标为(1,2);
(2)因为点P的“a系联动点”的坐标为(x+ay,ax+y),“-a系联动点”,的坐标为(x-ay,-ax+y),且点P的“a系联动点”与“-a系联动点”,均关于x轴对称,所以x+ay=
x-ay,
ax+y-ax+y=0,因为a≠0,所以y=0,所以点P分布在x轴上.
(3)因为在(2)的条件下,点P与原点不重合,点P的“a系联动点”
是点Q,不妨设点P(x,0),所以点Q的坐标为(x,ax),所以直线PQ平行y轴,所以PQ=|ax|,OP=|x|,
因为PQ的长度是OP长度的3倍,所以|ax|=3|x|,因为x不为0,所以|a|=3,
所以a=3或a=-3.
23.
解:(1)由A、B两点的纵坐标相同可知:AB∥x轴,∴AB=12﹣(﹣8)=20;
(2)过点C作l⊥AB于点E,连接AC,作AC的垂直平分线交直线l于点D,
由(1)可知:CE=1﹣(﹣17)=18,AE=12,设CD=x,∴AD=CD=x,
由勾股定理可知:x2=(18﹣x)2+122,∴解得:x=13,∴CD=13,
24.
解:
(1)AB=
=5;
(2)因为直线AB平行于y轴,所以AB之间的距离为|5-(-1)|=6;
(3)因为AB=
=5;AC=
=5;
BC=
=6所以AB=AC=5,所以三角形ABC是等腰三角形.
过点A作AD⊥BC,垂足为D,则BD=CD=3,所以AD==4,
所以三角形的面积为=12.
一、选择题(精心选,答案唯一,每题3分,满分30分)
1.下列描述中,能确定位置的是
(
)
A.小明的电影票是第三排
B.小亮的家在小明家的西北方向
C.轮船A在B港南偏东50°方向,同时在C港北偏东60°方向
D.
北京大兴国际机场在北京的南面
2.
(2019?株洲)在平面直角坐标系中,点A(2,–3)位于哪个象限?(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.
(2019?浙江杭州)在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则
( )
A.m=3,n=2
B.m=-3,n=2
C.m=2,n=3
D.m=-2,n=-3
4.已知点A(3,m),B(3,n),则下面说法中,正确的是
(
)
A.A,B一定不是同一个点
B.经过A,B的直线平行于x轴
C.
经过A,B的直线平行于y轴
D.A,B两点可在x轴的负半轴
5.
(2019?浙江丽水)如图1是雷达屏幕在一次探测中发现的多个目标,其中对目标A的位置表述正确的是
( )
A.在南偏东75°方向处
B.在5km处
C.在南偏东15°方向5km处
D.在南偏东75°方向5km处
6.
(2019?甘肃)已知点P(m+2,2m﹣4)在x轴上,则点P的坐标是
(
)
A.(4,0)
B.(0,4)
C.(﹣4,0)
D.(0,﹣4)
7.
已知点A(,|a|),则点A的位置是
(
)
A.第一象限
B.第四象限
C.第一象限或x轴的正半轴
D.
第四象限或x轴的负半轴
8.已知点A(x,
)在坐标轴上,则满足条件的点A的个数为
(
)
A.1个
B.
2个
C.
3个
D.
4个
9.
已知点M(2a-1,3a+2),N(-1,4),且直线MN∥y轴,则的值为
(
)
A.0
B.1
C.
D.
?
10.如图2,已知点A(3,0),点(-3,0),点P是△AOB内部一点,且坐标为(a,b),
则点P在△O内的对应点的坐标为
(
)
A.(b,a)
B.(-a,b)
C.
(a,-b)
D.
(-b,a)
二、填空题(仔细填,考虑全,每题3分,满分18分)
11.
(2019?山东省济宁市
)已知点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),
写出一个符合上述条件的点P的坐标
.
12.
如图3是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么第一架轰炸机C的平面坐标是
.
图
3
13.如图4是利用网格画出的太原市地铁1,2,3号线路部分规划示意图.若建立适当的平面直角坐标系,表示双塔西街点的坐标为(0,-1),表示桃园路的点的坐标为(-1,0),则表示太原火车站的点(正好在网格点上)的坐标是
.
图
4
14.
(2019?甘肃省庆阳市)中国象棋是中华名族的文化瑰宝,因趣味性强,深受大众喜爱.如
图5,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,﹣2),“马”位于点
(4,﹣2),则“兵”位于点
.
15.
(2019?山东临沂)在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是
.
16.
已知点A(3,4),B(a,4)之间的距离为4,则a的值为
.
三、解答题(规范解,求准确,满分52分)
17.
(满分6分)(2019?湖北黄石)若点P的坐标为(,2x﹣9),其中x满足不等式组,求点P所在的象限.
18.
(满分6分)
如图6,在6×6网格中,填写不同的汉字,并且每一个汉字都对应一个密码,如“国”的密码是(3,5),“涛”的密码是(5,3),当你理解了密码后,请把下列密码翻译出来,连起来读一读,猜猜他们是谁?一定会有惊喜.
(1)(3,6),(4,2),(5,1);
(2)
(2,1),(1,4),(5,6);
(3)
(3,1),(5,2)和(1,6);
(4)(6,5),(4,1),(2,2),
(4,1),(1,2),(1,6).
19.
(满分6分)
已知四边形ABCD各顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0)
(1)请建立平面直角坐标系,并画出四边形ABCD.
(2)求四边形ABCD的面积.
20.
(满分6分)如图7,分别作出△PQR关于直线m(直线m上各点的横坐标都为1)和直线n(直线n上各点的纵坐标都是-1)对称图形,它们的对应点的坐标之间有什么关系?
21.
(满分6分)
如图8,三角形AOB中,A、B两点的坐标分别是(2,4),(6,2),求三角形AOB的面积.
22.
(满分7分)
在平面直角坐标系xoy中的点P(x,y),若点Q的坐标(x+ay,ax+y),其中,a是常数,且a≠0,则称点Q是点P的“a系联动点”.例如,点(1,2)的“3系联动点”点Q的坐标为(7,5).
(1)点(3,0)的“2系联动点”的坐标为
;若点P的“-2系联动点”的坐标为(-3,0),
则点P的坐标为
;
(2)若点P的“a系联动点”与“-a系联动点”,均关于x轴对称,则点P分布在
;
请证明这个结论;
(3)在(2)的条件下,点P与原点不重合,点P的“a系联动点”
是点Q,且PQ的长度是OP长度的3倍,求a的值.
23.
(满分7分)
(2019?河北省)勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图9(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为
km;
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为
km.
24.
(满分7分)先阅读下列一段文字,再解答问题
已知在平面内有两点,,其两点间的距离公式为,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为或
(1)已知点,,试求,两点间的距离;
(2)已知点,在平行于轴的直线上,点的纵坐标为,点的纵坐标为,试求,两点间的距离;
(3)已知点,,判断线段,,构成三角形的形状?并求图形的面积.
参考答案:
一、选择题
1.C
2.
D
3.
B
4.C
5.
D
6.
A
7.
C
8.C
9.
B
10.B
二、填空题
11.
解:(1,﹣2)(答案不唯一).
提示:∵点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),
∴x>0,y<0,∴当x=1时,1≤y+4,解得:0>y≥﹣3,∴y可以为:﹣2,
故写一个符合上述条件的点P的坐标可以为:(1,﹣2)(答案不唯一).
12.
解:(2,﹣1).
13.
解:(3,0)
提示:双塔西街点的坐标为(0,-1),桃园路的点的坐标为(-1,0),所以大南门为坐标原点,所以太原火车站的点(正好在网格点上)的坐标(3,0).
14.
解:(﹣1,1).
15.
解:(-1,2).
提示:设点P(4,2)关于直线x=1的对称点坐标为Q(,2),根据题意,得,解得,=-2,所以点P(4,2)关于直线x=1的对称点坐标为Q(-1,2).
16.
解:a=-1或a=7.
三、解答题
17.
解:,解①得:x≥4,解②得:x≤4,则不等式组的解是:x=4,
∵=1,2x﹣9=﹣1,∴点P的坐标为(1,﹣1),∴点P在的第四象限.
18.
解:由“国”的密码是(3,5),“涛”的密码是(5,3),
知道,密码的设计是:第一个数字所在的列,与第二个数字所在行的交叉点上的字,就是我们需要的答案,根据这条原则,我们不难解答给出的问题.
(1)祖冲之;
(2)
陈景润;
(3)笛卡尔;(4)《中学生学习报》.
19.
解:
(1)建立坐标系如下:
(2)如图所示,分割图形后,得四边形的面积=80.
.
20.
解:
仔细观察坐标系,得P(-1,3),Q(-4,5),R(-4,1),设P(-1,3)关于直线m=1的对称点的坐标为(,3),根据对称等距性,得-1=1-(-1),解得=3,所以(3,3),
同理可得,(6,5),(6,1),所以△PQR关于直线m的对称图形为△;
仔细观察坐标系,得P(-1,3),Q(-4,5),R(-4,1),设P(-1,3)关于直线n=-1的对称点的坐标为(-1,),根据对称等距性,得3-(-1)=-1-,解得=-5,所以(-1,-5),同理可得,(-4,-7),(-4,-3),所以△PQR关于直线n的对称图形为△;作图如图所示;
21.
解:
方法1:
如图1,过点A作AE⊥y轴,垂足为E,过点B作BD⊥x轴,垂足为D,二线交于点C,因为点A的坐标为(2,4),所以点E的坐标为(0,4),所以OE=4,因为点C在直线AE上,所以点C的纵坐标为4;因为点B的坐标为(6,2),所以点C的横坐标为6,所以点C的坐标为(6,4),
所以AE=-=2-0=2,AC==6-2=4,CB==4-2=2,BD==2-0=2,OD==4-0=4,所以四边形OECD的面积为:6×4=24,===4,===4,===6,
所以=四边形OECD的面积---=24-4-4-6=10.
方法2:
如图2过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,因为点A的坐标为(2,4),所以点C的坐标为(2,0),所以OC=2,AC=4,因为点B的坐标为(6,2),所以点D的横坐标为6,所以点D的坐标为(6,0),BD==2-0=2,OD==6-0=6,CD==6-2=4,所以===4,
===6,直角梯形ABDC的面积为:=12,
所以=直角梯形ABDC的面积+-=12+4-6=10.
22.
解:
(1)因为x=3,y=0,a=2,所以x+ay=3+0×2=3,ax+y=3×2+0=6,
所以点(3,0)的“2系联动点”的坐标为(3,6);
因为点P的“-2系联动点”的坐标为(-3,0),所以x-2y=-3,-2x+y=0,所以x=1,y=2,
所以点P的坐标为(1,2);
(2)因为点P的“a系联动点”的坐标为(x+ay,ax+y),“-a系联动点”,的坐标为(x-ay,-ax+y),且点P的“a系联动点”与“-a系联动点”,均关于x轴对称,所以x+ay=
x-ay,
ax+y-ax+y=0,因为a≠0,所以y=0,所以点P分布在x轴上.
(3)因为在(2)的条件下,点P与原点不重合,点P的“a系联动点”
是点Q,不妨设点P(x,0),所以点Q的坐标为(x,ax),所以直线PQ平行y轴,所以PQ=|ax|,OP=|x|,
因为PQ的长度是OP长度的3倍,所以|ax|=3|x|,因为x不为0,所以|a|=3,
所以a=3或a=-3.
23.
解:(1)由A、B两点的纵坐标相同可知:AB∥x轴,∴AB=12﹣(﹣8)=20;
(2)过点C作l⊥AB于点E,连接AC,作AC的垂直平分线交直线l于点D,
由(1)可知:CE=1﹣(﹣17)=18,AE=12,设CD=x,∴AD=CD=x,
由勾股定理可知:x2=(18﹣x)2+122,∴解得:x=13,∴CD=13,
24.
解:
(1)AB=
=5;
(2)因为直线AB平行于y轴,所以AB之间的距离为|5-(-1)|=6;
(3)因为AB=
=5;AC=
=5;
BC=
=6所以AB=AC=5,所以三角形ABC是等腰三角形.
过点A作AD⊥BC,垂足为D,则BD=CD=3,所以AD==4,
所以三角形的面积为=12.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
